Epicycloidal Movement
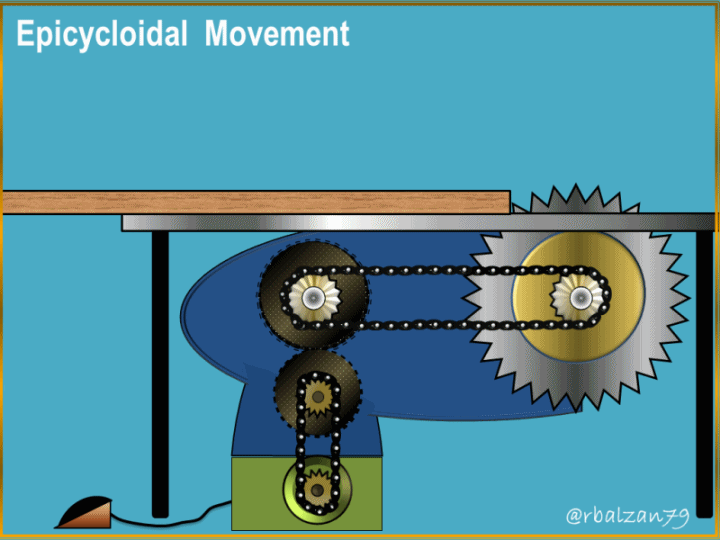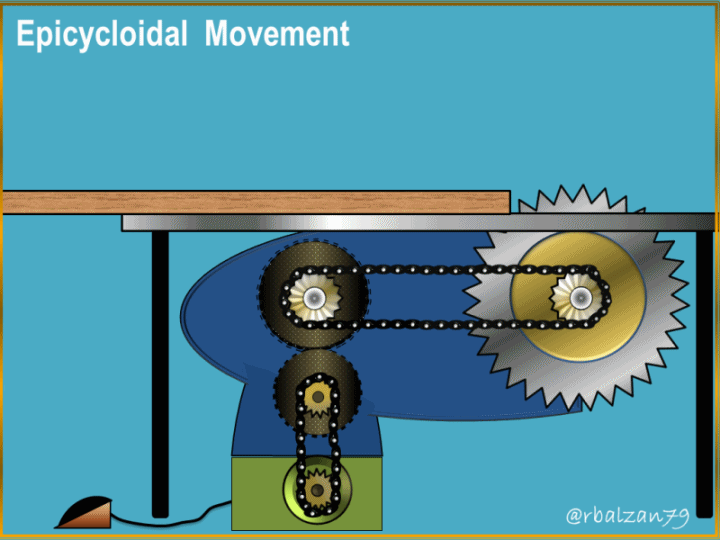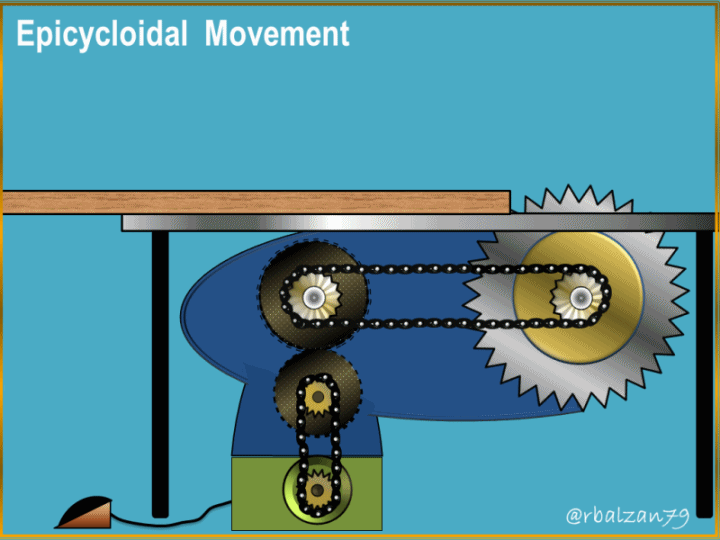
Greetings to the entire academic and scientific community of steemit.
Introduction
We continue to observe our environment with the aim of being able to capture any type of mobility that forms part of our existence, and we have already been able to demonstrate that the phenomenon of movement is indispensable both for all living species and for the universe itself; therefore, it is necessary to be able to expand our knowledge of this phenomenon.
Until now we can say that we have been based on the analysis of basic movements such as circular, parabolic, elliptical and hyperbolic, through these we find other mobilities such as oscillatory movement, vibratory, wave, reaching other phenomena such as chaotic, forced harmonic and cycloidal cushioning, all of them vital to our lives.
From the cycloidal movement we could know that it is generated following the trajectory of a curve which originates when allowing to roll without slipping a certain circumference on a straight surface, this curve with important characteristics like the brachistocrone and tautocrone, such aspects differentiate them from the other curves and from the same straight, since the cycloid turned out to be the fastest trajectory even that the same straight trajectory.
Now we continue to analyze the marvelous cycloid curve, but this time the curve will not be generated on a straight surface, but on another surface equal to the one that generates this curve, that is to say, a circumference. From there we put the prefix Epi (of Greek origin, generally used to indicate that something is on something else) before the phenomenon of mobility to be studied on this occasion, that is to say, the epicycloidal movement.
Therefore, in a specific way we can express that the generation of this curve differs from the cycloid with respect to the surface on which the other circle rolls, that is to say, there are two circles, this makes the epicycloid curve represent the geometric place of the different positions of any point belonging to the circle that turns, revolves or rolls externally on another similar figure, this does not mean that both have the same diameter always.
It is important to note that depending on the proportion between the radii or diameters involved, i.e. both mobile (generating) and fixed (guiding) circumferences, we can obtain different curves belonging to the epicycloids. Therefore, by observing a certain circumference rolling over another we can imagine the formation of any of these curves.
The generation of these curves has allowed the creation or design of important mechanical systems which man has implemented to transmit a set of particular movements and combine them to achieve a certain objective, such as, for example, the epicycloidal train implemented in automobile mechanical systems.
To be more precise, this wonderful curve is fundamental for the design of gear teeth, and when referring to the epicycloidal movement, we can say that this represents the observed mobility of a gear wheel on another and this with the purpose of being able to transmit a certain necessary rotary movement within a machine or any mechanical system, that is to say, it allows to give revolutions or turns to other elements that compose a complex mechanical system.
We have been able to notice and verify that each one of the trajectories has defined the mobility phenomena previously analyzed, for example, the circular and circumferential movements, the parabolic and parabola, the elliptic and ellipse, and so on, highlighting in this way that from the geometric places described by each movement we can originate its denomination.
As with the previous mobilities, the epicycloidal phenomenon does not escape from the aforementioned characteristic, and therefore it is important that we can know in a general way the trajectory of its path, this through the use of two circles as we can see in the following figure 1.
Figure 1. Directive circle and generator circle, point (P) generator of the Epicycloid
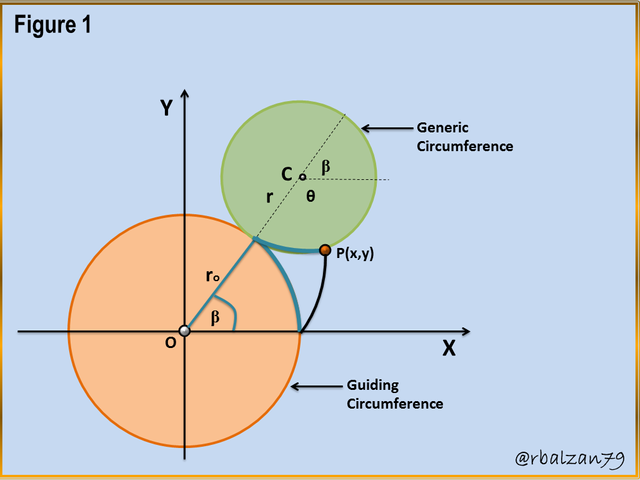
In the previous figure 1, we can visualize the formation of a type of epicycloid curve, however, it is important to take into account the relationship in the proportion between the radii or they can also be the diameters of the circles involved, that is, the one that moves (generatrix) and the fixed or immobile one (directrix), According to this reason or proportion, the shape of the epicycloid varies; therefore, if the radius of the directive circumference is three, four or five times greater, we will obtain epicycloidal figures similar to a flower, either with three, four or five petals, and so on.
This as for the formation of any epicycloidal curve and the same implemented in the analysis of the epicycloidal movement and its essential applications in various mechanical systems with gears, many examples of such systems can be found in our environment including in our so precious home.
Epicycloidal Movement
When a certain epicycloid curve is generated, it is necessary to highlight the movement carried out by a certain circumference (generatrix), where one point of this turns on another circumference (directrix), thus taking away the epicycloidal movement. These curves are also known as mechanical curves due to their great importance in the creation or design of gear parts, and these are used in essential movement transmission systems.
We call all those elements or components that make up a certain machine mechanisms, and with these systems it is possible to transmit different types of movements such as the case of the two circles when forming or giving rise to the epicycloid, this action could represent two cogwheels.
We know that the wheels can be found in various machinery or mechanical systems achieving improved movement of objects with the application of the least amount of effort, it is important to know the generation of some of these epicycloidal curves as we will see in the following figure 2.
Figure 2. Generation of the nephroid
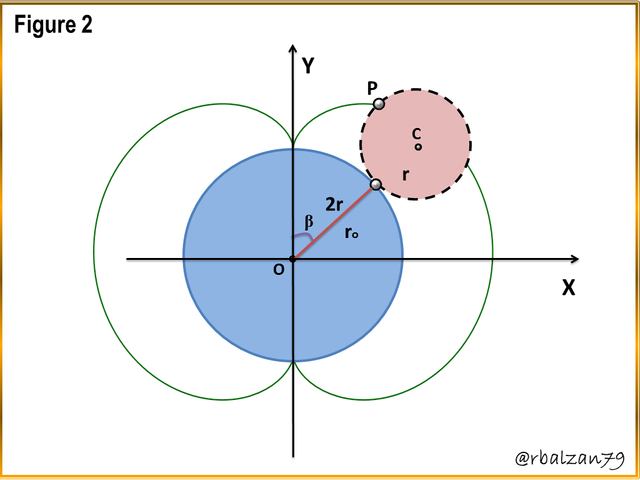
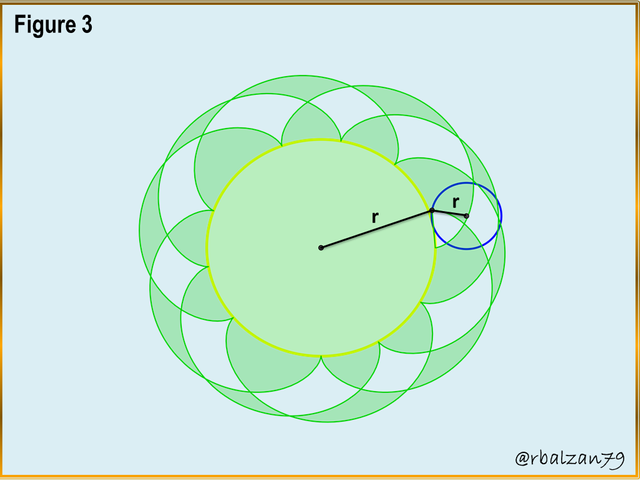
This type of epicycloidal curve, the nephroid, has two points or two arcs, this is because the radius of the generating circle is twice smaller than the radius of the directive circle, however, we can have much more complex proportions between these radii of the circles involved, where, the radii of such circles can be immeasurable or unlimited so that the epicycloid originated by such circles never closes, that is, there will be no end to its points, arcs or loops, as we can see in the following figure 3.
Figure 3. Generation of epicycloids with multiple points or arcs
In the fascinating world of automotive mechanics, epicyclic gear systems are very well known and they are extraordinary mechanisms used to vary the speed of cars. This important characteristic makes these systems very useful in the general behaviour of the global system of such automotive machines.
When talking about gears anyone should know what is being pointed out since many of the equipment, devices or mechanical systems in our homes are equipped with these wonderful elements, therefore, it is important to be able to point out some of these types of components in the following figure 4.
Figure 4. Some Types of Gears

In the previous figure 4, we could know some gears that are implemented in transmission systems or mechanisms of any type of mobility, especially combined or complex movements, and thus be able to perform any particular task, but all our activities can be said to revolve around the necessary implementation of these gears, then we will show one of many utilities of these elements in our lives as we can see in the following figure 5.
Figure 5. Some gear combinations develop epicycloidal motion
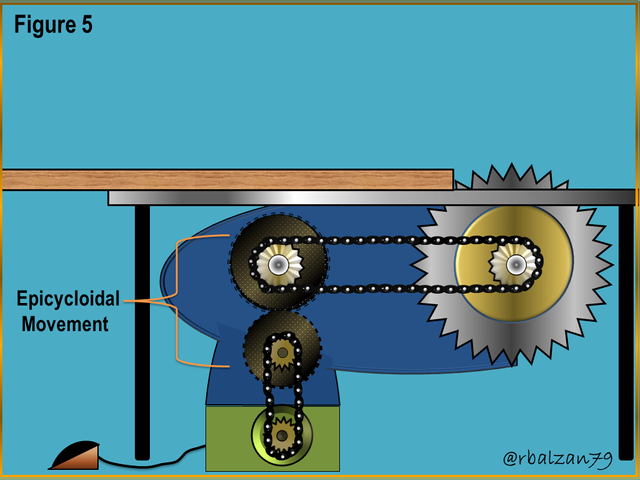
In the previous figure 5, we could observe its essential implementation in some activity of our daily life, but lots of examples like this we can find around us and at any moment, the other thing to emphasize is that we could verify besides the combination of some of these pieces carry out the movement analyzed in this opportunity, that is to say, the epicycloidal movement, demonstrating in this way its vital utility in the life of the man.
Extraordinary applications of the epicycloidal movement through the use of circular gears in various devices that give us greater stability and comfort in our development, any of us has been able to observe a beautiful compilation of pieces of circular gears, where we can imagine the generation of any epicycloid at the time of carrying out clear is to the epicycloidal movement, this we can visualize in the following figure 6.
Figure 6. Circular gear parts assembly. Public domain image, Pixabay

Conclusion
We continue to see that everything around us can carry out some kind of movement in order to be able to develop some kind of activity, and even to be able to keep every living species in this universe alive, since everything we know requires any kind of movement.
This is how fascinating movement is, and therefore, we must always highlight any kind of knowledge that we can obtain from this phenomenon. In this opportunity we analyze the wonderful epicycloidal movement and its great importance in the development of our most essential activities as we could observe it through the use of gear parts in mechanical systems.
This type of curve can also be called a mechanical curve, thanks to its relationship with the design of the aforementioned pieces for simple or complex gear systems. The truth is that everything in our environment that is mechanical includes any piece of gearing and especially those of the circular type, thus highlighting the practicality originated by the mobility between two elements of circular geometric shapes, toothed or not, one on the other.
It is important to continue highlighting the usefulness of the knowledge related to basic movements such as circular, parabolic, elliptical and hyperbolic, thanks to them we have been able to configure mobilities such as the one analysed on this occasion, that is to say, the epicycloidal movement generated by the movement of two circular forms one over the other as it was possible to point out in each of the previous figures, as well as all the positive aspect that the same (epicycloidal movement) has given us throughout all these years.
Until another opportunity my appreciated friends and readers of steemit, very specially to the members of the wonderful communities friends of #steemstem and #curie, for which I recommend widely to be part of these exemplary projects, because they highlight the valuable work of the academy and the scientific field.
Note: All the images of my authorship were elaborated using the applications, Power Point, GeoGebra and the animated gif with the PhotoScape application.
Nice post...
Thank you for your visit. Greetings.
@tipu curate
Upvoted 👌 (Mana: 15/20 - need recharge?)
Thanks @byercatire for the support. Greetings.
Esta publicación ha sido votada por el Equipo de Steemitas Club. Gracias @rbalzan79 por compartirnos esta publicación.
Steemitas Club es un proyecto que ofrece delegaciones gratis de 100 SP para los nuevos usuarios y además cuenta con un proyecto de curación para apoyar el contenido original.Thanks to @SteemitasClub community for your support. Greetings.
Excelente trabajo, gracias por compartir.
Thanks to you @amart29 for your support. Greetings.
Excellent description of the Epicycloidal movement. Thanks for sharing on steemit @rbalzan79
Thanks friend @carlos84 for your support. Greetings.
Excellent.
I shared this work from my Twitter account: https://twitter.com/lupafilotaxia/status/1234313877317455876
Thanks friend @lupafilotaxia for your support. Greetings.
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the steemstem.io app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM.
Thanks to the communities of @SteemSTEM, @curie y @minnowbooster for the support received.