What exactly is an orbit? An Introduction
After several very busy weeks and a Physics GRE, I finally have another article. Today I'd like to discuss the basics of (gravitational) orbits - namely, why they occur at all and how they work.
This introduction will assume you know absolutely nothing about orbits. If you already have some background but want to learn more about non-circular orbits, skip to the section titled Classical Orbital Elements.

Early image of the ISS, in a low, mostly circular orbit above Earth. The ocean can be seen several hundred kilometers below.
Credit
What is an orbit?
Much of the technology you use everyday depends on the fact that satellites can be put into stable orbits. When someone drives to work, the navigation system routing them around traffic is using GPS satellites to pinpoint the user's locations. Digital maps themselves rely on pictures taken by satellites to plot terrain and display aerial views. Even things like weather forecasts and television often rely on satellites.
Each and every satellite, including the International Space Station, travel above Earth in semi-stable orbits, brought about by how the gravitational force works. There is in fact gravity in space - if could stand on a platform that went up to the space station, you would weigh about 90% of your weight at sea level. The gravitational force between you and Earth gets weaker as you get farther away from the planet, but it never actually goes away (although you can get to a point where it is insignificant).

The Hubble Space Telescope as seen from a US shuttle as it orbits Earth
Credit
When an astronaut feels weightless on the space station, it is really because there is no "ground" to push back on them. When you feel your weight pushing you into the ground, you are actually feeling the ground pushing back at you (known as a "normal force"). Imagine jumping onto a sheet of paper suspended above the ground - you would break right through, and wouldn't feel weight at all until you hit the hard ground below. This is also demonstrated by the feeling of lightness you can get when an elevator descends, since you experience less force.
What this means is you can only feel weight at all when you are being pushed into something. If you jump in the air, you will have a brief moment of weightlessness as you fall back down. If you could theoretically fall forever, you would never feel any weight at all.
But, in fact, you can - all an object in orbit is doing is really just falling ... forever.
Falling into an orbit
Imagine that you are standing in a field and you throw a ball straight out away from you. The ball's horizontal velocity is unchanged by gravity (since it acts down), but the ball gains vertical velocity over time as gravity accelerates it down, resulting in it eventually crashing down. The ball always lands back at the level of the ground.
But now say the field is curved. Now if I throw the ball, after some time it will crash down slightly lower than where the ground originally was, because the ground has "curved down" under it. This also means it will take slightly longer to fall.
But the planet itself is curved! So imagine I throw a ball straight away from myself on the perfectly smooth surface of Earth. It will fly forward and eventually fall away from me, slightly lower than me. Now I throw another ball, harder this time. It falls a little further away, and a little further down.
Okay, now pretend that there is no air anywhere on the air and I throw the ball incredibly fast. It is now going so fast that as it falls down, the ground curves away from the ball at the same rate as it is falling. Gravity turns the ball's direction of motion, but the ground itself is also "falling away", so the direction of gravity changes. As the ball keeps falling, it never reaches the ground because the ground is curving away equally fast.
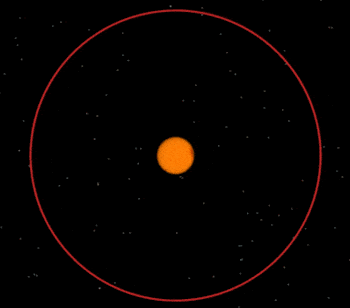
Drawing of a circular orbit above a star. The object in orbit falls under the star's gravity but never reaches the constantly curving ground.
Credit
And what happens in this case? If the ground curves away from the ball just as quickly as the ball falls, the ball will cross the entire surface of the Earth, come back, and hit me in the head right at the spot where I threw it from (this, as you will see, would be just a bit painful).
That is really a circular orbit is: Falling in such a way that your altitude drops at the same rate as the planet curves, allowing you to fall indefinitely.
Practical Circular Orbits
Of course the example I just mentioned is impossible. The form of the gravitational force as described by Newton lets you actually calculate the speed required to orbit a planet in a circular orbit. There is just one speed possible for any given distance from the surface of a planet, and for an orbit to be perfectly circular that speed must be directed in a very specific direction: Perpendicular to the planet's surface. The equation ends up being:
v = sqrt(G*M/r)
Where "v" is the required velocity for a circular orbit, "G" is the universal Gravitational Constant, "M" is the mass of the planet (in this case Earth), and "r" is the distance from the orbiting object to the center of the planet - not the surface!
Doing the math for Earth gives a single velocity required to orbit the planet at sea level: Around 8 kilometers per second. This lets you cross through most cities in a matter of seconds, cross countries in minutes, and cover entire continents in less than a quarter of an hour. A bullet from a rifle usually comes in under 400 meters per second - 20x less than required to orbit. Needless to say, if you actually got something going that fast at sea level it would be instantly incinerated by heating from the atmosphere, and would probably produce a large explosion.
But if we go up higher, we don't have to deal with the atmosphere. Above about 100km, the air is thin enough that objects can stay in orbits for a reasonable amount of time before re-entering the atmosphere due to drag. At these low altitudes, each orbit takes about 90 minutes to completely circle the planet. A rocket can fire tons of hot gas out of the back through a nozzle to produce a force pushing it and a satellite up to the speeds necessary to keep the satellite in space.
Once a satellite is in orbit, it will "fall forever" as previously described. Gravity is still there, and it's almost as strong as it is on the ground, but the satellite never feels any weight, and it won't ever hit the ground unless it is slowed down by drag or other minute effects.
Does an orbit have to be a circle?
No - in fact, nothing ever actually orbits in a perfect circle. The most general stable orbit is an elliptical orbit (hyperbolic and parabolic orbits exist as well, although these trajectories involve the object escaping the gravity of the selected planet...), with the "focus" (essentially one of two 'centers' of the ellipse) being the planet in question.
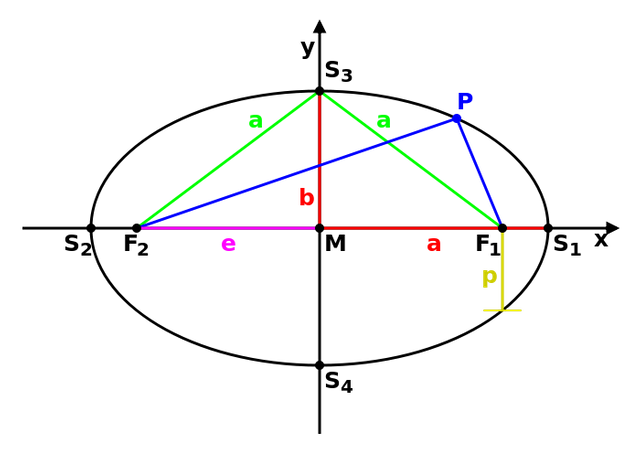
The geometric ellipse almost perfectly describes any real orbit. The planet being orbited would lie at one of the two foci, F1 or F2.
Credit
Every single satellite orbiting Earth or planet orbiting the Sun travels in an elliptical orbit. These orbits can be very close to circles, but they will always be at least slightly elliptical.
The result of an elliptical orbit is that the object moves faster near the planet (the closest point is called "perigee" for Earth) and slower further away (the far point is called "apogee" for Earth).
But now we need a better way to describe these orbits. With circles, you can just specify the radius and now you know the speed anywhere along the orbit. For ellipses, this becomes much more difficult. Thankfully there is something to help.
Classical Orbital Elements
Any orbit - circular, elliptical, parabolic, hyperbolic - can be described by six unique numbers known as classical orbital elements, or COEs. All you need is a single position and speed of an orbiting object and you can find all six COEs, uniquely determining the orbit the object is travelling in. To be excessively brief, the six elements are:
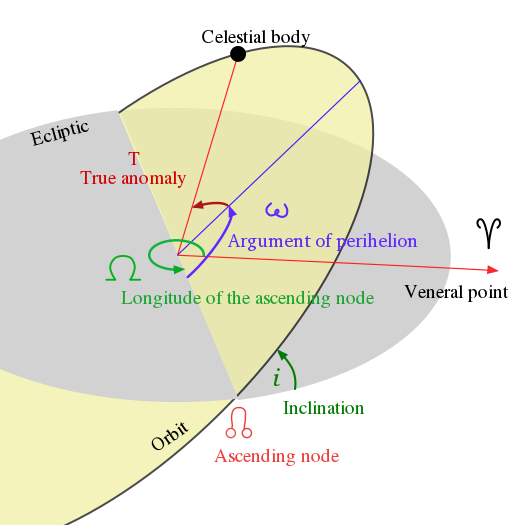
Four of the Classical Orbital Elements illustrated
Credit
Semimajor Axis - Essentially the half-width of the ellipse, labelled "a" on the ellipse diagram above.
Inclination - How "tilted" the orbit is relative to the equator. 90-degree-inclination orbits are known as "polar orbits" because they pass over the north and south pole, while 0-degree-inclination orbits stay exactly above the equator.
Eccentricity - How "stretched" the ellipse is. An eccentricity of zero indicates a circular orbit, while an eccentricity of 1 indicates a parabolic orbit (this means that the object is perfectly escaping the pull of Earth's gravity). Between 0 and 1 we find elliptical orbits - the closer the eccentricity is to 0, the more the ellipse looks like a circle.
Right Angle of the Ascending Node - An angle that describes how much the orbit is rotated about a certain reference point.
Argument of Perigee - An angle that describes where the perigee - the point where the object is closest the central planet - is relative to a reference point.
True Anomaly - Where exactly the object is along its orbit. With no orbital perturbations (small forces that change the orbit), True Anomaly is the only element that changes with time.
All of these elements have precise mathematical definitions and I've described them a little too simply to avoid over-complicating this post. If you're interested in learning more, I've attached a reference at the end of the post. If you look on a website like Heavens Above you can see some of these elements for the satellites flying above your head (and even look up times to see them for yourself!)
Conclusion
From here, a discussion of orbits will need to involve actual math and more involved calculations, although they really aren't that bad if you're interested in learning more. I encourage you to keep learning more if you are interested, and I'd be happy to answer any questions. I hope that I was able to at least somewhat clarify the concept of an orbit if you hadn't seen how they work in the past.
As always, let me know if you have any questions, comments, or corrections.
Thanks for reading!
Additional Reading and Sources:
NASA Orbital Elements
Braeunig Orbital Mechanics
HyperPhysics - Earth Orbits
Fundamentals of Astrodynamics and Applications, D. Vallado
(I used this book in some of my orbital mechanics courses - it's very math-heavy and probably isn't for beginners but if you have some physics/math background it is an excellent resource)
Bravo, good article. Glad to see you back posting stem articles. Just one clarification in your diagram it references perihelion and argument of perihelion. Perihelion is closest approach to sun, perigee typically references other bodies like the earth. Periastron is typically used for stars.
Good catch - I used to use peri/apoapsis for generality but slipped into the habit of calling everything -gee from my orbits classes recently.
Thanks for this! I've been trying to wrap my head around the COEs ever since reading Seveneves, and it's helping.
Hi, I found some acronyms/abbreviations in this post. This is how they expand:
Not too shabby!