How to shout a secret message to a stranger in public and understand each other such that nobody else has a clue? By stranger, I mean someone you haven't communicated with before in any form.

If you answered "by encrypting your message", how would you share the key of the encrypted message in public, when shouting out is your only way of communicating? If you simply shout the encryption key, then everyone else will also know the key, and therefore there would be no point in encrypting your message. So the aim would be to share the key over a public channel such that only you and the person you are communicating with gets the key. Diffie-Hellman key exchange does exactly that.
You might get surprised to learn how often this algorithm is used. When you browse a website which requires a secure channel, say Amazon, to prevent anyone else(like the Internet service provider, or the government, or someone else on your Wifi network etc.) from knowing your credit card details, the communication between you and Amazon needs to be encrypted.

image source pixabay.com

But for you and Amazon to understand each other's encrypted messages, both of you should know the key. As I said earlier, sending the key directly over unsecured channel would be meaningless. One option would be to meet with someone from Amazon and exchange the keys. But this is rather impractical, given the number of people Amazon would have to meet, and the number of other people you would need to meet(as you need secure channels for everything from Steemit to Facebook). This is where Diffie-Hellman key exchange comes to the rescue!

I will now give the most common analogy given, as to how Diffie-Hellman key exchange works.
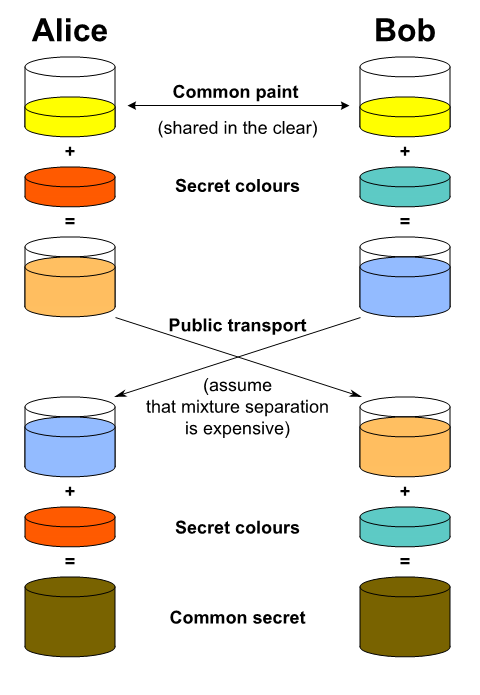
Suppose Alice and Bob want to share a secret. However, Eve is snooping on their exchanges and can watch and copy everything that Alice and Bob send each other. So, if Alice sends Bob a message, Eve can read it. So, Alice and Bob need to create a key, such that Eve isn't able to know it. Let's use colours instead of numbers and letters for the sake of understanding.

So, Alice and Bob announce to each other 'yellow' to be their starting colour. Eve also copies yellow.

Now Alice and Bob independently choose a secret colour which they don't share with each other. Eve isn't able to know their secret colours. Suppose, Alice chooses orange and Bob chooses blue. Now, Alice and Bob mix yellow with their secret colour to obtain orange-tan and light-blue respectively.

Source: By Lorddota - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=62609302

Alice and Bob then send their respective mixed colours to each other. Eve gets them both too. Now Alice adds her secret colour to the colour that Bob sent her. Similarly, Bob adds his secret colour to the mixed colour he received from Alice. Hence Alice and Bob now share a secret colour which Eve doesn't know. They can now use this as the key for their encrypted messages and Eve can't understand it as she doesn't have the key!

This exchange worked because:

• Paint(colour) was easy to mix.
• But Paint was difficult to unmix.
• The final colour was independent of the order of mixing but dependent on the amount of mixing.

Now let's see how it is actually done. The commonly used function is the discrete logarithm function. In principle, you can use anything that is easily computable and gives same result independent of the order, but very difficult to invert or guess the input from the result. Click here if you want to get an idea about modular arithmetic before we get into the details.
The basic idea is like this:

1. Alice(or Bob) chooses two prime numbers g and p and tells them to Bob.
2. Now Bob chooses another secret number, say, 'b'. He computes B=g^b mod p then sends B to Alice.
3. Alice chooses her secret number 'a' and computes A=g^a mod p. She then sends A to Bob.
4. Now Alice computes B^a mod p and Bob computes A^b mod p i.e.:

• Bob gets:
  
  A^b mod p=(g^a mod p)^b mod p= g^(ab) mod p
  
• Alice gets:
  
  B^a mod p=(g^b mod p)^a mod p= g^(ba) mod p
  
  But we know that g^(ab)=g^(ba), so both Bob and Alice arrive at the same number

C=g^(ab) mod p= g^(ba) mod p,
but anyone listening to their exchanges can't get the same number without the secret numbers. Now using C as the key they can send messages via whichever symmetric encryption like AES, Blowfish etc. whichever they decide and rest of the world would be clueless what they are talking about.

It is important to note that in practice g, p, a and b are usually 100s of digits long making it very difficult to crack. The function is such that Eve cannot use A and B to obtain C. Also, note that Diffie-Hellman algorithm is not being used for exchanging messages but to create a shared encryption key which is subsequently used to exchange encrypted messages.

Feel free to ask in the comments if you failed to understand some part.

References

• Diffie–Hellman key exchange

---

---

Found the post interesting? Read about how clocks and Mathematics are closely related in my previous post: Clocks and Mathematics

Follow me at @omstavan for more such posts!