What does the AC0 complexity class mean?
AC^0 is a circuit complexity class. It represents the set of decision problems that are solvable with a family of constant-depth unlimited-fanin polynomial-size circuits.

Photo by Yung Chang on Unsplash.
Unpacking that:
- “Circuit”: a boolean function created with logic gates and wires.
- “Decision problems”: yes-or-no answers to whether a particular bit-string belongs in some set. However, in practice we will also talk about “functions” in AC^0 as well that output more than one bit.
- “Family”: unlike automata which have unbounded input, a circuit has only a fixed number of inputs. So to solve a problem of length n, we need a circuit with n inputs, and for a problem of length n+1 we need a circuit with n+1
inputs. Instead of specifying a single machine, we’re actually specifying an infinite number of machines, one for each input size. - “Constant-depth”: the depth of a circuit is how many gates there are between any input and the output. So, circuits in this family must have a maximum depth, no matter how large n gets.
- “Unlimited-fanin”: each of our logic gates may take as many inputs as desired. (Some complexity classes only allow two-input gates.)
- “Polynomial-size”: the total number of gates is bounded by some polynomial in the size of the input, n.
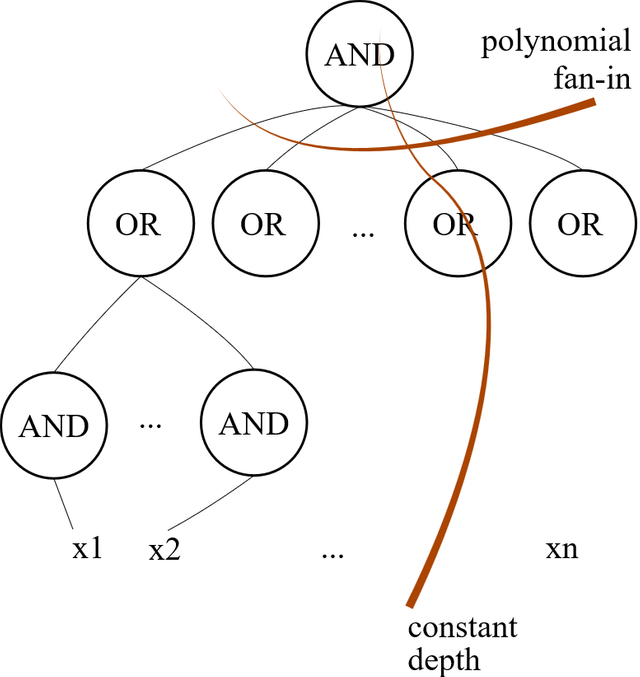
Diagram from Wikimedia Commons
Circuit families in AC^0 are sometimes required to be "uniform." A “uniformity” condition on circuits means that the circuit description can be generated by a Turing machine (usually subject to some resource constraints), given the size of the input. But in other contexts, a problem could be in AC^0 even if its circuit family was uncomputable. Conventions vary, so it's best to be explicit.
An example problem in AC^0: addition, or as a decision problem, “is x + y = z a valid addition”? (Note that propagating the carries one by one, like a ripple-carry adder, doesn’t work for AC^0 because that is a non-constant-depth construction.)
The canonical problem not in AC^0: computing the parity of the input.
AC^0 is the smallest member of the "alternating complexity" class AC^i, which are polynomial-sized circuits with depth (log n)^i.
Originally answered on Quora: https://www.quora.com/What-does-the-AC0-complexity-class-mean/answer/Mark-Gritter
Further reading:
I wonder when these type of questions start appearing on musing so they can be answered there instead of on quora.
@stemq is actually a better home, but it seems doubly-redundant to ask a question there just to answer it myself (two separate posts) when I already answered it once on a different site. But the volume of questions on stemq is pretty low, and the quality of questions interesting to me on @musing is not high.
This story was recommended by Steeve to its users and upvoted by one or more of them.
Check @steeveapp to learn more about Steeve, an AI-powered Steem interface.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!