Lower bounds on time complexity
I'm (slowly) continuing to read The Computational Complexity of Logical Theories, and it came in useful answering this Quora question: Can we predict [time] complexity before writing an algorithm? Here's an explanation of a theorem from the book that gives a way to establish a computational complexity lower bound.
Reducibility
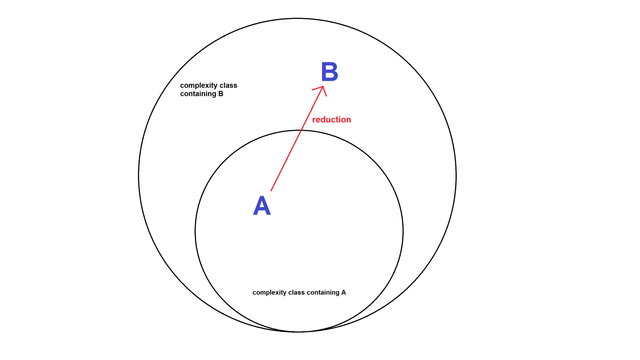
A decision problem A can be reduced to another B if we can write an algorithm to translate any problem in A into an equivalent problem in B. That is, x is in A if and only if f(x) is in B. When f can be computed in polynomial time, this is known as a "Karp" reduction. In contrast, a "Cook" reduction is one in which we may use B many times as a subroutine.
In the book, Ferrante and Rackoff distinguish between "logspace" reductions which use a logarithmic amount of space and "polylin" reductions which use a linear amount of space, but polynomial time. The latter term seems to have fallen out of favor. An additional technical restriction on reductions is that the output problem should be linear in the length of the input problem (rather than trying to hide a non-linear factor by making the problem much larger.)]
A reduction gives a bound on time and space complexity. If a language A is polynomial-time reducible to B then:
- If
Bis in a complexity class, thenAmust be in that time complexity class as well, plus the cost of conversion if applicable: this is an upper bound onA. - If
Ais not in a given time complexity class, thenBcannot be in that time complexity class either: this is a lower bound onB.
Lemma 4.4 in [Ferrante 1979] spells this out in more detail:
(Theorems typeset by the author, using LaTeX on overleaf.com)
Finding counterexamples
If we want to use the lemma above to find a lower bound (the "contrapositive" part) then we need to a decision problem not in a complexity class. Fortunately, there's a way to do this nonconstructively: the Time Hierarchy Theorem. This theorem says that there is a separation between different time-based complexity classes; that is, some time complexity classes are strict subsets of others. A "strict subset" just means that there is one element in the larger set that's not in the smaller set--- so, we don't necessarily know what that language is, but we can appeal to its existence!
Formally, for determinstic Turing machines, the theory says DTIME( o( f(n) / log f(n) ) ) is a strict subset of DTIME( f(n) ). Here, DTIME( f(n) ) is the class of decision problems (languages) recognizable by a deterministic Turing machine in time bounded by f(n), where n is the input size. o( x ) is little-o notation which is an asymptotic bound.
For nondeterministic Turing machines the inclusion is even simpler: NTIME( f(n) ) is a strict subset of NTIME( g(n) ) whenever f(n) is o( g(n) ). So there are problems that run in time n^3 but not n^2, n^4 log log n but not n^4, and 2^(2^n)) but not 2^(2^(n/2))).
The last example shows a notational difficulty; if we want to deal with repeated exponents, or tetration instead of exponentiation, it'll be better to write things using Knuth's up-arrow notation. Briefly, a ↑ b = a^b, a ↑ b ↑ c = a^(b^c), and a ↑↑ b = a raised to itself, b times.
Now we can state Lemma 4.5 that is introduced by [Ferrente 1979] without proof; today we recognize it as a straightforward consequence of the Time Hierarchy Theorem:
We can make similar statements about other complexity classes like DTIME.
NTIME-hardness and Lower Bounds
Now we're ready for a theorem that can actually do some work, the one I quoted in the Quora answer linked above.
Before we used reductions on individual decision problems, so what does it mean for NTIME(f(n)) to reduce to L_0? That requires that every problem in the class has a reduction to L_0. We say that such a language is "hard" for the class. For NP, such problems are called "NP-hard", but we can have a "NTIME(2^n)-hard language as well. (A language which is both part of a class C and a member of class C is called "C-complete".)
The proof of this theorem is very simple, but feels like magic. We use lemma 4.5 to fix some other language L that is in NTIME( f(n) ) but not NTIME( f(n/2) ). But L_0 is hard for NTIME( f(n) ), so L_0 reduces to L. Then we can use lemma 4.4 to get the lower bound.
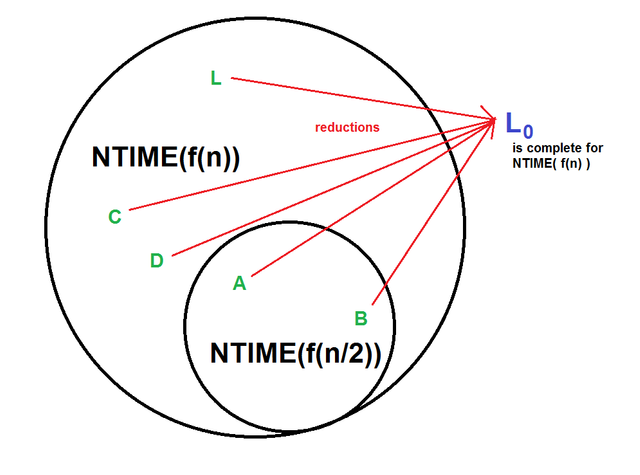
(Diagram by the author, should be "hard for NTIME" not "complete for NTIME", sorry.)
Now, this doesn't guarantee that L_0 is actually in NTIME( f(cn) ); it just can't be any easier than that. The property of being NTIME-hard is very strong. From a practical point of view, it's now feasible to start showing that interesting decision problems are "hard", and out pops the appropriate lower bound. For example, the logical theory of integer addition is NTIME(2^(2^n))-hard, so deciding it must be at least as difficult as NTIME( 2^(2^(cn)) ).
Sources
Jeanne Ferrante, Charles W. Rackoff, "The Computational Complexity of Logical Theories" (Lecture Notes in Mathematics: 718), Springer-Verlag, 1979.
Weisstein, Eric W. "Knuth Up-Arrow Notation." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/KnuthUp-ArrowNotation.html
Wikipedia, Polynomial time reduction
Wikipedia, Time hierarchy theorem

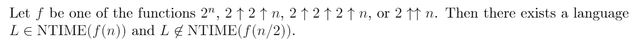
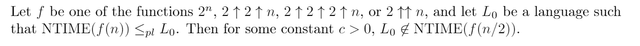
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Hi @markgritter!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV