THE CALCULATION IN PHYSICS WITH THE FEYNMAN DIAGRAMS
Since the mid-twentieth century, theoretical physicists have increasingly turned to Feynman diagrams to address complicated calculations, in which the highest accuracy has been sought. These diagrams have come to revolutionize the most varied aspects of physics.
Richard Feynman presented his diagrams in the late 1940s, offering them as an accounting device that simplified the cumbersome and complicated calculations of Quantum Electrodynamics (QED), but they were soon employed in nuclear and particle physics, as well as in state physics. solid. And it is that the integrated expressions of Feynman accentuated the spatial-temporal "pictoriality" of the events.
Actually, Feynman's contribution is highly original. The processes visualized in the Feynman diagrams have become indispensable in almost all the domains of physics. The propagators, which carry the shock particles in shock, go from being complicated distributions in space-time (Schwinger) to simple rational denominators (Feynman propagators) in "space of moments". The complicated perturbative calculations of higher orders are summarized in a rule (from Feynman) that is read directly from the diagrams.
In QED, electrons and other fundamental particles exchange "virtual" photons that serve as force carriers. These virtual particles take their energy from the vacuum, for the short time allowed by the Heisenberg Uncertainty Principle.
There were two fundamental problems that frustrated the calculations in the QED. The first is that as soon as one proceeded beyond the simplest degrees of approximation, it stopped offering finite answers, and the infinities, logically, lacked physical sense. The second was that the formalism was very uncomfortable, "an algebraic nightmare with endless terms to take into account and evaluate". Since electrons could exchange any number of these virtual photons, the more photons intervened, the more complicated the corresponding equations were. In the calculation, each situation had to be taken into account and all contributions added up. But, the reality is that this infinite number of different contributions in practice could be truncated after a few terms, which constituted the so-called method of "calculation of disturbances"; However, this apparently simple method presented extraordinary difficulties. For example, a calculation had been made in e4 in the mid-1930s, and then hundreds of different terms appeared. And each contribution to the total calculation occupied more than four or five lines of mathematical symbols, so it was very easy to omit terms. Summing up: unresolved divergences and unapproachable accounts.
As I said, Feynman diagrams are a very powerful tool to make calculations in quantum theory, which allow us to overcome the two problems described above. Like any calculation in quantum, it is a question of obtaining a complex number, or "amplitude", whose squared modulus gives a probability.
The amplitudes in the QED are composed of some basic ingredients, which have their own associated mathematical expression, for example:
the amplitude of a virtual electron traveling from x to y. B (x, y),
the amplitude of a virtual photon traveling from x to y. C (x, y);
and the amplitude of the electron and the photon colliding eD (where e is the charge of the electron).
In the dispersion of an electron by an electromagnetic field, the field can be described as a collection of photons. In the simplest case the electron will collide only once with a single photon
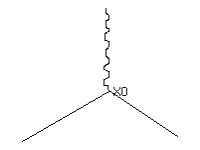
in a single vertex X0. Here, only the real particles, so that the only contribution to the amplitude comes from the vertex: A(1) = eD.
But other complex phenomena can happen to the electron, such as the incoming electron can detach from a virtual virtual before colliding with the electromagnetic field and reabsorb the virtual photon at a later point
In this diagram, the electron lines and the photon lines are in three places and, therefore, the amplitude for this contribution is proportional to e3. So the amplitude will be A(2) = e³ ∫ DB (1,0) DB (0,2) DC (1,2).
And at the next level of complexity there are up to seven different Feynman diagrams.
The total amplitude of an electron interacting with the electromagnetic field would then be written:
And the probability of interaction |A|².
The set of amplitudes for the various possible initial and final states constitutes a type of matrix whose "rows" and "columns" correspond to a basis for final and initial states, respectively, a matrix known as a dispersion matrix, or simply an S matrix, and the calculation of the S matrix is considered the main objective of the QFT (Quantum Field Theory).
Each choice of Feynman diagram topology represents an ordinary integral of finite dimension, which can be treated by the powerful methods of the complex contour integral.
In the QED (Quantum Electrodynamics) all the divergent parts of the Feynman diagrams can be assembled in several "packages", so that the infinites simply provide "rescalation" factors that can be ignored according to the process known as renormalization (there are cancellations mutuals according to certain principles of symmetry of the standard model).
The starting point for the diagrams is an appropriate Lagrangian; Feynman diagrams would then represent a perturbative development of the quantum theory associated with said Lagrangian, which in essence is only a series development of powers of some parameter, or parameters, which in this case is the coupling constant. In the QED is the electric charge e. At each vertex of a Feynman diagram there is a factor e, so that the terms of the series are diagrams with an increasing number of vertices, that is, the diagrams of n vertices provide together the coefficient of in.
The QFT is constructed from a Lagrangian, by the formulation in terms of Feynman path integrals or sum of Feynman stories, which of course is also the basis of the Feynman diagrams. And it is that in the quantum world, instead of only a classic "reality" represented by a trajectory (a history), there exists a great complex superposition of all the "alternative realities". Each story is assigned a complex weighting factor, which we call an amplitude, and the total is normalized to the unit module.
The role of the Lagrangian is to tell us what amplitude should be assigned to each of these stories.
By knowing the Lagrangian ℒ, the action S can be obtained for said history. The complex amplitude is then given by the formula
But since there is an infinite continuum of classical alternatives, the amplitude should be considered as an "amplitude density".
But, the path integrals for individual quantum particles are mathematically better reflected by replacing the uncontrollable collection of stories by what is called the Feynman propagator.
In the case of a Dirac particle (for example, an electron) the propagator in the space of moments takes the form i(P -M + iε), where P = γª Pa, being the quantity Pa the 4-moment that has the particle for the chosen path. (ε is taken as a very small positive real number, as an artifice to guarantee the positive/negative frequency requirements of the Feynman propagator).
- We know that in the dispersion of electrons the dispersion matrix can be described by the expression
<f | s | i> where f is the final state and i is the initial state.
| sfi |² is the probability of the transitions in the perturbative development of the dispersion matrix S. It means that if before the collision the system were in a state Φi (certain set of free particles), the probability amplitude of its passage to the state Φf (another set of free particles) is the matrix element Sfi.
In this electron dispersion is obtained at the end for the dispersion amplitude (since electric waves are flat waves)
The photon propagator has been introduced here in the representation of impulses
Each of the two terms of amplitude (i) can be represented symbolically in the form of the so-called Feynman diagrams.
I'm talking about the dispersion represented in the following diagram
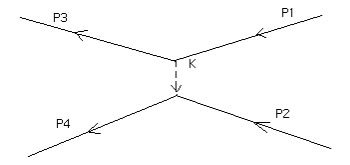
which corresponds to the first term of (i)
A factor γ is associated to each vertex of the diagram (points of intersection).
The lines of continuous line "incidents", which are directed to a vertex, correspond to the initial electrons and are associated to the u-factors the bispinorial amplitudes of the corresponding electronic states. The lines that start from the vertices or "emergent" correspond to the final electrons, which are associated with the factors u. The indicated factors, when "reading" the diagram, are written from left to right in the order that corresponds to the movement along the lines of continuous lines and in the opposite direction to the arrows. The vertices are joined by a dashed line that corresponds to a virtual (intermediation) photon, "emitted" at one vertex and "absorbed" at the other; the factor i Dmn (k) is associated to this line.
The impulse of the virtual photon k is determined by the conservation of the impulse at the vertex. That is, k = p1-p3 = p4-p2.
In addition, the common diagram is assigned a common factor (-ie) 2, where the exponent is the number of vertices in the diagram.
(Taken from the work "Relativistic Quantum Theory" by Beresteiskii, Lifshitz and Pitaeuskii).
Much better is to go to the description made by Feynman himself of the electron-electron collision
Source
In the figure, an electron (continuous line in the lower right) emits a force-transmitting particle-a virtual photon represented by the wavy line-that impinges on the second electron (continuous line in the lower left). The first electron recedes and the second is deviated from its original trajectory. It would be the quantum mechanical version of the repulsion between particles endowed with the same charge.
The emission or absorption of a photon by an electron is associated with a factor e γm, where e is the charge of the electron and γm a vector of Dirac matrices (arrays of numbers linked to the spin of the electron). By giving up part of its energy and momentum, the electron on the right moves from x6 to x4, experiencing a certain "backspace" and change of direction. The one on the left, after absorbing the photon, gaining some energy and momentum, disperses from x5 to x3.
According to Feynman, this diagram represents the mathematical expression
expressed in K + and δ + factors.
Feynman called K + (5,1) the probability of moving the electron as a free particle from point x1 to x5. The other incoming electron moved freely - with probability K + (6.2) - from point x2 to x6. This second electron could then emit a virtual photon in x6, which in turn would move - with probability δ + (S562) - up to x5, where it would be absorbed by the first electron.
Elevating the expression (ii) squared gives a fairly good estimate of the probability of two electrons colliding, but since the two electrons can exchange any number of photons, (ii) represents only the beginning of the calculation.
Feynman used his new diagrams to describe the different possibilities, for example, there are nine different ways that electrons can exchange two photons, each with four vertices (their mathematical expressions, then, contain e4 instead of e2). The mathematical contribution of each of these diagrams is constructed by introducing K + and δ + for each line of electron and photon and connecting them at the vertices with the factors eγm.
The charge of the electron (e) is small: e2≃1 / 137, in appropriate measures. Since the charge of the electrons governs the intensity of their own interaction with the photons that transmit the force, whenever the pair of electrons exchanges one more photon, these equations that describe the exchange gain another factor that multiplies by that small number e2. That is, the contribution of the double photon exchange is not one hundredth of the contribution of the exchange of a single photon. The term that corresponds to the exchange of three photons (with a factor e6) is ten thousand times less than the term corresponding to the exchange of a photon, and so on. Therefore, in practice the calculation is truncated after a few terms to obtain a sufficient approximation.
Feynman also applied a "renormalization", or combination of "calculation tricks" to eliminate the "infinities" that appeared in the integrals of the diagrams of two and more photons. Feynman's method took into account the order of operations; I started from the diagrams as a mnemonic aid to write the pertinent integrals, and then I modified them to remove them, one by one, the infinities.
Actually the extension of the Feynman diagrams owes very mainly to Freeman Dyson from the Institute of Advanced Studies of Princeton. In an article of Physical Review he compared Feynman's methods, and the theories of Schwinger and Tomonaga, demonstrating the mathematical equivalence of the three methods.
Dyson deduced rules for the use of diagrams, offering a "use" guide that included instructions, step by step, of how to draw the diagrams and translate into their associated mathematical expressions. He also generalized the analyzed examples, demonstrating that the problems of Quantum Electrodynamics (QED) could be renormalized.
From these results, the use of Feynman diagrams can be extended to other areas, for example, to scalar electrodynamics involving charged mesons and photons.
For the study of processes associated with this last interaction, the development of the collision matrix can be used
Applying this formulism to charged pion systems, making q = -e (e> 0), b † would create a negative pion p- and a † a positive pion p +.
Lagrangian density remains
ℒi = -ie: (f + θmf - f θmf +) Am: + e2: A2f +:.
Being f the mesonic constant.
It would have two types of vertices
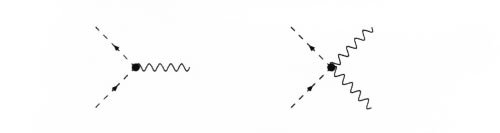
In one, two mesonic lines (straight dashed lines) and a photonics (wavy line) converge and it is of order e. In the other flow two photonic lines instead of one and is of order e^2.
- Since the initial and final states of a certain matrix element are specified, in addition to the spin or polarization state, for its moments, it makes the calculation of such element in the space of moments simpler.
This work is very good and should be better valued. I leave you my vote.
Maybe you are interested in my work of electromagnetism, I am also posting for steemstem.