Sequence And Series : A Simple Introduction
Hello and a warm and lovely greetings to all steemians. It's me @leoumesh and today I am gonna be giving a very brief introduction on mathematical sequence and series.
So lets begin with the very topic.

What is Sequence?
The idea of a sequence originates in the process of counting in a very natural way. During counting, we begin with the number 1. The number is followed or succeeded by the number 2, 2 by 3, 3 by 4, 4 by 5, and so on. This is how we arrive at the succession of counting numbers beginning with the number 1. One of the conventional ways of representing the succession of counting numbers is to list the first few numbers separated by commas and then write dots at the end to indicate the remaining numbers. Thus we have the symbolic representation:
in which the numbers are in the given order : 1 is followed by 2, 2 by 3, 3 by 4 and so on. Some other examples which contain the same idea are:
I. Set of even numbers : 2 , 4 , 6 , 8 , 10 , .....
II. Set of positive integral of powers of 2 : 2, 22 , 23 , 24 , 25 , ......
III. Set of reciprocals of positive integers: 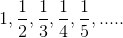
These are possibly some of the simplest and best known examples which gave rise to the following definition of a sequence:
This is a classical definition of sequence. Its modern version is based on the definition of a function and is indeed defined as a special kind of function.
A sequence is a function defined on the set Z = {1 , 2 , 3 , 4 , 5 , ...} of positive integers.
We denote the function (sequence) by the symbol f. Then its value at 1 , 2 , 3 , 4 , 5 , ..., n , ...... are f(1) , f(2) , f(3) , f(4) , ..., f(n) , .... respectively. These values make up the range :
of the sequence f. The elements of the range , i.e., f(1) , f(2) , .... are called the terms of the sequence f.
An important point to be noted is that we have considered the entire set of positive integers as the domain of definition of the sequence. If the domain consists of a finite number of elements only, the sequence is said to be finite, otherwise the sequence is said to be infinite.
Types of Sequences
Various types of sequences are known but we will be dealing with a few specific types of sequences only. They are arithmetic sequences, geometric sequences and harmonic sequences.
I. Arithmetic Sequences
A sequence of numbers in which a certain number can be added to (or subtracted from) any term to get the next term is called an arithmetic sequence (or arithmetic progression). In other words, a sequence in which the difference between successive terms always has the same value is called an arithmetic sequence. For example:
(a). 1 , 3 , 5 , 7 , 9 , ......
(b). 1 , 4 , 7 , 10 , .....
(c). -9 , -6 , -3 , 0 , 3 , ......
(d). a+2b , 3a+b , 5a , 7a-b , ....
II. Geometric Sequences
A sequence of numbers in which every term after the first may be obtained by multiplying the preceding term by a certain number is called a geometric sequence (or geometric progression). In other words, a geometric sequence is a sequence of numbers in which the ratio of any term to its preceding term is always the same. Examples of such sequences are:
(a). 1 , 2 , 4 , 8 , 16 , .....
(b). 3 , -9 , 27 , -81 , .......
(c). 1 , x , x2 , x4 , x6 , ......
III. Harmonic Sequences
A sequence is said to be a harmonic sequence if the reciprocals of its terms form an arithmetic sequence. The harmonic sequence is also known as harmonic progression. Some examples of harmonic sequence are:
(a). 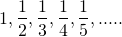
(b). 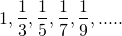
(c). 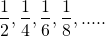
Series
A sequence may be finite or infinite. Given a finite sequence such as
1 , 2 , ...... , 5 or 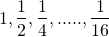
we can form such as
1 + 2 + ..... + 5 or 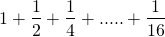
From elementary arithmetic, we know that
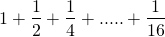 =
= 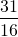
The expressions 1 + 2 + ..... + 5 and 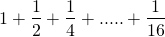 are called the series associated with the sequences 1 , 2 , ...... , 5 and
are called the series associated with the sequences 1 , 2 , ...... , 5 and 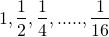 respectively.
respectively.
In series, the terms of sequence are connected by addition and subtraction signs. In general, if a1, a2 , a3 , ..... , an denotes a finite sequence, the symbolic expression a1 + a2 + a3 + ..... + an is called a finite series associated with the sequence.
In other words, the expression a1 + a2 + a3 + ..... + an represents the sum of the n terms of the sequence {an}.
A short hand notation for the sum a1 + a2 + a3 + ..... + an is
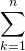 ak
akwhere 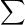 is the capital Greek letter sigma, and
is the capital Greek letter sigma, and 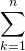 ak is read, 'the sum of ak as k goes from 1 to n'.
ak is read, 'the sum of ak as k goes from 1 to n'.
The symbol kis called the variable of summation or a dummy suffix. Moreover, the sum is denoted by the symbol Sn. Thus,
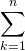 ak
akIf the sequence is an infinite sequence a1, a2 , a3 , ..... , an , ..... then the symbolic expression a1 + a2 + a3 + ..... + an + ..... is called an infinite series. As a simple example of an infinite series, we have
associated with the infinite sequence of the natural numbers {n}. There is an important difference between the finite and infinite series. In former case, elementary arithmetic provides us with a unique number called the sum of the series. But in the later case, no process of elementary arithmetic will yield such a sum.
Arithmetic Sequences and Series
An arithmetic sequence has the property that the difference between two successive terms ( any term subtracted from the following term ) is always the same. This difference is called the common difference. We shall use the following notations for terms and expressions involved in an arithmetic sequence and series.
In terms of these notation, the arithmetic sequence and associated arithmetic series may be written in the following way:
Arithmetic sequence : a1, (a1+d) , (a1+2d), ........ , (an-d), an
Arithmetic series: a1 + (a1+d) + (a1+2d)+ ........ + (an-d) + an
We now give some formulae connecting the various terms mentioned above.
| The common difference | d = ak+1 - ak , k>=1. |
|---|---|
| General term of the arithemtic sequence | a1 + ( n -1 )d |
| Sum of first n terms of the arithmetic series | Sn=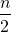 (a1+an) = (a1+an) = 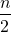 [2a1 + (n -1 )d] [2a1 + (n -1 )d] |
Properties of Arithmetic Sequence
The following are the properties of an Arithmetic Sequence (AS):
I. If each term of an AS be increased or decreased by a constant number, the resulting numbers are in AS with the same common difference before.
II. If each term of an AS be multiplied or divided by a constant number, the resulting numbers are in AS with a common difference equal to that of given AS multiplied or divided by the corresponding constant number.
So , if a, b , c , d , ...... be an AS and k is a constant number not equal to zero, then
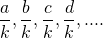 are each in AS.
are each in AS.Geometric Sequence and Series
A geometric sequence has the property that the ratio of any term ( except the first) to its preceding term is always the same. The ratio is called the common ratio and is denoted by r. We follow the same notations as used in the case of an arithmetic sequence and series. Here also, we give some formulae connecting the terms, number of terms, sums, common ratio etc.
| The common ratio | r = ak + 1 / ak, k>=1. |
|---|---|
| General term of the geometric sequence | an = a1rn-1 |
| Sum of first n terms of the geometric series | Sn = 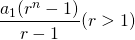 |
| Sum of first n terms of the geometric series | Sn = 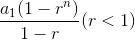 |
| Sum of first n terms of the geometric series | Sn = 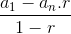 |
Properties of Geometric Sequence
The following are the properties of a GS :
I. If each term of a GS is multiplied or divided by a constant number , the resulting sequence is also a GS.
II. If each term of a GS is raised to a constant power , the resulting sequence is again a GS.
Thus if a , b , c , d , ...... be a GS and k is a constant number not equal to zero , then
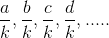 is a GS.
is a GS.Harmonic Sequence and Series
A sequence of numbers will form a harmonic sequence (HS) if the sequence of the numbers formed by taking the reciprocals of the term forms an AS ( Arithmetic Sequence). There are no formulae connecting the terms , number of terms , sum in harmonic sequence. Since to every HS, there always corresponds an AS , the terms of HS are determined with reference to the corresponding AS. So , we follow the same notation as in the case of AS.
Properties of Harmonic Sequence
If each term of an HS be multiplied or divided by a constant quantity, the sequence of the resulting numbers is also in HS. So , if a , b , c , d , ...... be an HS, and k a constant quantity not equal to zero , then
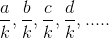 is again an HS.
is again an HS.The introductory part has already got too long. So, hopefully in my next article or post, I am gonna give introduction to means and will be deriving the formulae for means and show relationship between arithmetic means, geometric means and harmonic means.
Thank you for taking your time in reading this article. Please feel free to comment and interact.
References
https://www.mathplanet.com/education/algebra-2/sequences-and-series/arithmetic-sequences-and-series
Mathematical expression coded on : http://www.quicklatex.com/
steemstem

SteemSTEM is a community driven project which seeks to promote well-written and informative Science, Technology, Engineering and Mathematics ( STEM ) posts on Steemit. The project involves curating STEM-related posts through upvoting, resteeming, offering constructive feedback, supporting scientific contests, and other related activities.
DISCORD: https://discord.gg/j29kgjS
@leoumesh Thanks for this great elaboration the basic terminology and notation of sequences and series, including summation symbols about sequence and its properties.
Thank you sir for yourprecious comment😀🙂
Your work is great, lets see if others have better post than you or else we will give you 0.1 SBD. Seriously your work is great if it is written by you !
We need more steemians like you, definitely you will succeed one day, if you do the same !
We think your post deserves our help for today !
0.1 SBD is transferred to your account !
Thank you @teamnepal
Welcome, it's our pleasure !
Please do take your deserved SBD time to time !
thanks @leoumesh for this great explanation about sequence and series.. helped me a lot ...
You are welcome any time🙂