Breaking Down Barriers - Quantum Tunneling

Based on the title, you may have thought that this could be a personal development article. But this is not a personal development article. We will not try to overcome our problems with others with different quantum mechanical methods. This article deals with quantum tunneling, which is a usual effect in everyday life, different and extraordinary but atomic dimensions, as well as passing through walls without breaking them down.

---

---

It is obvious what happens when you can not get the corner while going to work and drive your car towards the garden wall of the corner apartment. You would hit that wall. If you are faster enough, you will bulldoze through it. But try it as much as you wish, you can not go through that wall without damaging your car or the wall. If you can not jump over the barriers in a 400-meter hurdle, you can not overcome the run. It is quite obvious, right? It is possible that we can explain all these phenomena, which govern our daily life and rely on our common sense, with classical mechanics (Newton) in physics which the physical system be founded and developed by Galileo in the 1600s and Newton in the 1700s.

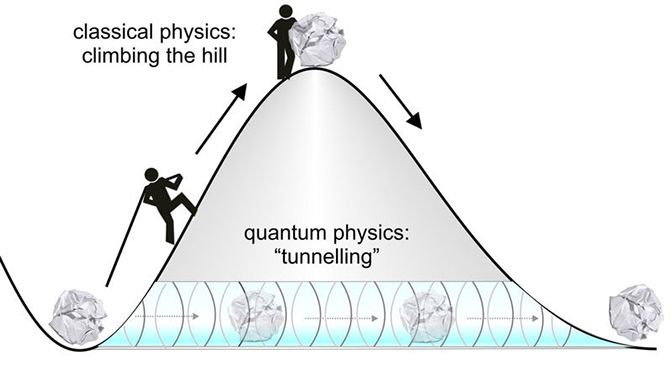
When we try to explain the behaviors of the atoms with the Newtonian physics we are accustomed to, phenomena that are unlikely to occur within the boundaries of the classical physics become quite unusual. Today we are explaining all this with quantum mechanics. Here is the decision of the quantum mechanics about these barriers we just mentioned. All the particles (and indeed everything) have the possibility of overcoming obstacles when the energies are not enough (if they do not jump as high as they can). But how? To understand this, we have to go a little deeper into the quantum mechanics.

---

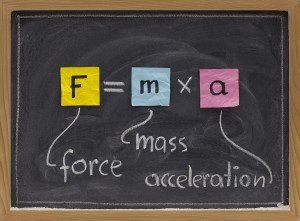
First, let's see what quantum mechanics gives us. Our primary goal in mechanics is to find out how objects behave under force and displacement. For this, we have to use the mass equation (Newton's 2nd Law) found by Newton in classical mechanics, and we need to solve this equation for the forces we know. To solve this equation for matter-acting forces is simply to find the path that this matter will follow in time. So, after we leave a ball at a certain height, we find exactly where and how fast it will follow the path it will follow. We have to solve the Schrödinger equation in quantum mechanics. The solution of this equation, unlike classical mechanics, gives the probability that matter with "m" mass exists at a certain point. In other words, we can not pinpoint exactly where the mass is by solving this equation. We can only calculate the probability of existing that point. Is this a lack of theory? No, it's not, is a result of nature's work. Classical mechanics, if I'm sitting in any seat, it will tell me I'm sitting on a seat right now. Quantum mechanics will most likely indicate that I am there. In short, we use quantum mechanics to obtain a probability distribution for our position. To understand exactly where we are, we need to make a measurement.

---

---

Measurement in quantum mechanics leaves very interesting, irreversible and unpredictable effects on the system. When you measure the position of a rolling ball, you have already set the point where the classical equations give you. But in a system that gives you a probability distribution like quantum mechanics, your measuring system changes dramatically and unpredictably. After you have solved the quantum mechanical equations and obtained the probability distribution for the place and after you measure the place I sit, you know now that I'm sitting on that seat. According to this situation, the quantum equation must give the same answer. That is, the accumulation of the probability distribution only on one point (the position of the seat), technically speaking, "collapses" at that point. So any measurement you calculate will cause the probability distribution to collapse to a point.

Let's try to summarize the probability wave function and its decay. You are solving the Schrödinger equation to know where I am. For example, suppose that this equation gives you different possibilities. These possibilities are available when you do not touch the system, so when you do not ask me that "where are you kedi?" When are you asking me where I am, then all these possibilities are gathered into a single situation within themselves, and you would also get it as a response.

Another interesting feature of quantum mechanics is that it never allows you to measure the position and speed of a particle at the same time with infinite precision. When you measure the position of any piece, you lose all your knowledge about its speed, and therefore momentum. In the opposite case, you do not know where is the particle that you have measured its speed. Heisenberg's famous uncertainty principle is exactly what it talks about. You can not pinpoint the position or speed of a particle at the same moment or the time or energy. If we continue with the seat example, Since you know I'm sitting on that seat, you have almost no knowledge of my speed. I might be stationary; I also might be going at speed close to the speed of light!

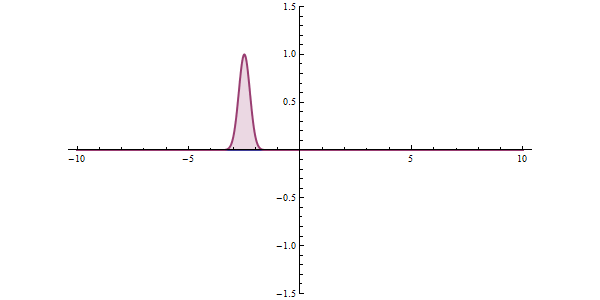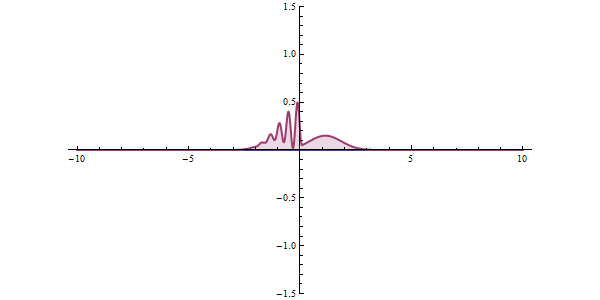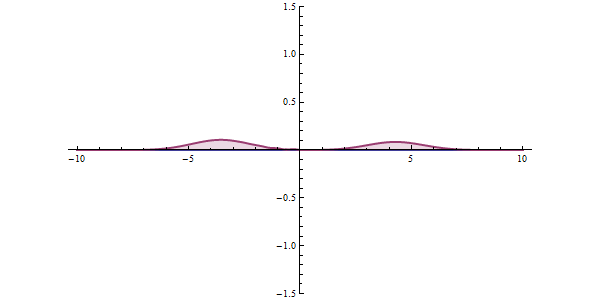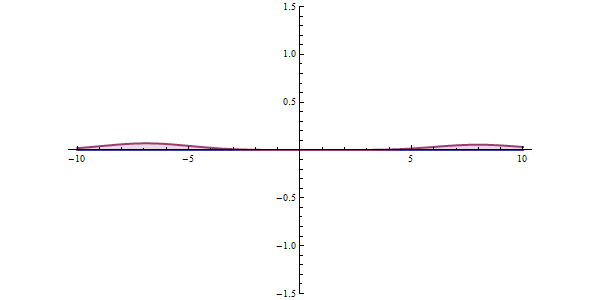
Well, what does all this have to do with tunneling? To understand this, let's examine a different example. The graphic shown in red in the animation is the probability of our particle being at any point. In classical mechanics, the only way to overcome this hurdle is to have the potential energy to overcome that hurdle. But things work differently in quantum space. There is an accepted approach to the subject. The measurement made can collapse the position of the particle to the right of the obstacle, and even if the particle is not the most energetic at first, it can clear the hurdle. This effect is called "Quantum Tunneling" in short.

How do we know the existence of a phenomenon that is so contrary to our common sense, or do we believe it only because of mathematical reasons? No. The systems built on the effect of quantum tunneling work just as we would expect. At this point, I would like to give two examples of the effects of quantum tunneling and of helping us. The first is the scanning tunneling microscope (STM) and second is the speed effect of chemical reactions.

A scanning tunneling microscope (STM) is an instrument for imaging surfaces at the atomic level. Its development in 1981 earned its inventors, Gerd Binnig and Heinrich Rohrer (at IBM Zürich), the Nobel Prize in Physics in 1986.*

It has a resolution that is high enough to determine the locations of the atoms on the surface one by one and to use them when necessary. The working principle basically depends on quantum tunneling. A very very thin (atomic-size) microscope tip is being built. Later, this tip is brought closer to the surface, and a potential difference is applied between the tip and the surface. If the tip is close enough to the surface, the electrons tunnel through the potential difference and allow a current to flow. This current is both measurable and depends on the tip position, the applied potential difference, and the density of the atoms on the surface. With STM, we can examine atoms on the surface one by one and examine them very precisely. Even, when we want it, we can move atoms on the surface as we want with this microscope.

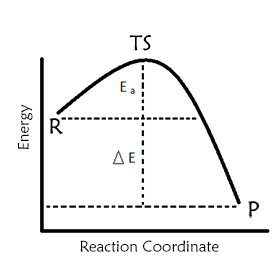
Another effect of quantum tunneling is the speed of chemical reactions. Especially in reactions based on the exchange of low-mass particles such as hydrogen or electrons, the quantum tunneling effect causes the reaction rate to go well beyond the classical estimates.
The graphic you see in the picture shows the potential energy graph for a classical reaction. The items shown in R indicate the substances that enter the reaction, P is products, and the TS indicates that the reaction has the minimum energy required to be achieved. In fact, this graph, as I mentioned earlier, constitutes a 'hindrance' to the reaction. Thanks to quantum tunneling, light particles such as hydrogen and electrons can go to these overcrowded products even if the energies are not enough and cause the reaction rates to be much higher than expected.

We can understand why we have not seen quantum tunneling in our everyday lives if we are to be at the very beginning. Like every quantum mechanical event, tunneling has the potential to happen. This probability is inversely proportional to the difference between the mass of the particle and the energy of the barrier and mass. So, the greater the difference in mass and energy, the lower the likelihood of tunneling. Of course, there is a possibility that a car drifting towards the wall will pass by tunneling. But since the mass of the car is too large for the mass of electrons, the probability of tunneling is almost zero. If you hit this possibility by slamming the wall once every second in the car, the time you will spend to tunnel to the other side will be even higher than the age of the universe!

---

Image Sources

• The futuristic tunnel has a bright light at the end.
• Newton's 2nd Law
• Quantum Physics - Tunneling Diagram
• Quantum Tunneling Animation
• Scanning Tunneling Microscope

---

References

• Chemical Kinetics and Reaction Dynamics. Paul L. Houston. Dover Books on Chemistry, 2001.
• https://en.wikipedia.org/wiki/Quantum_tunnelling
• https://en.wikipedia.org/wiki/Scanning_tunneling_microscope
• https://www.nobelprize.org/educational/physics/microscopes/
• https://chem.libretexts.org/Core/Physical_and_Theoretical_Chemistry/