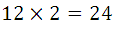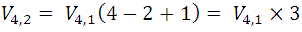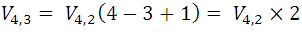Combinatorial theory: Variations
hello friends of steemit
Today I want to share with you a concern that I have always had with the possible combinations that can be done with certain objects, for example with my clothes, the order in which I place my favorite songs in the player, the way in which I have the furniture in my room to create more spaces and even the possible numbers that I can have with the date of my birth. There are many questions that I ask myself when I want to know. how to calculate those numbers ?.
I found the answer to this question in a simple and basic mathematical theory, called Combinatory Theory, to explain these concepts I will try to explain it as formally and appropriately as possible.
Source
Elements of the combinatorial theory
In arithmetic, the concept of the natural number is arrived at starting from the whole, without taking into account the nature of the elements that form it, nor the order of placement in which they are found. For example, the number 6 represents in abstract form all the sets of beings or objects that are coordinated with the A, B, C, D, F, regardless of the nature and order of the elements of said sets.
On the contrary, in the combinatorial theory, the order of placement of its elements and the various way of grouping them are considered in the sets. The simplest example is given by: Consider the figures 1,2,3 and 4, you can easily understand that it is possible to form many numbers with these figures, 123, 234, 341, etc, we will say that two of them are different under The following conditions:
- When they have some of the unequal figures
- when even having the same figures are placed in different order.
Given these conditions, 3 cases are presented, described as variation, permutation and combination
Variations
Then the conditions described presents a problem that is usually called Variation. The number of elements chosen from the given total, to form the different groups expresses the order of the variation, thus the different numbers of three figures that can be formed with the four mentioned above, constitute the variations of order 3 with 4 elements, or simply ternary variations of 4 elements, and are expressed by the notation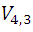 
. In general, the number of order variations n that can be formed with m elements with m> n is designated by 
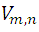(1).
Therefore the variations are defined as follows:
Given m objects, it is called variations of order n with m> n, to the groups that can be formed taking n of those m elements that they give us, so that any two of the groups are considered different when: a) differ in some element; b) if they have the same elements, they are placed in a different order
Formation of variations
The variations with a certain number of given elements can be formed successively by a uniform method, which consists of adding to each variation of a certain order each of the elements that do not appear in it. To see this we continue with our simple example:
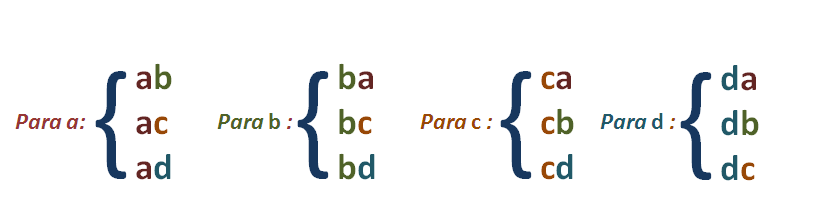
We want to determine the variations that can be formed with four elements a, b, c and d. We proceed as follows, for the variation of the first order it is clear that
For the binary variations or taken two to two, they are obtained from the previous ones, writing next to them, each one of the remaining elements like this:
As the first place of the binary variation can be occupied by any one of the four given elements: a, b, c, d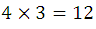 and once one of them is placed, there are three elements available to occupy the second place, for which is easy to understand that the total is (
) of binary variations of the four elements given.
For the variations taken from three to three, they are deducted from the binaries proceeding in a similar way, that is, writing each of the remaining elements after these last ones, thus:
as in this case, the remaining elements are two for each binary variation, they result, as can be observed, two ternary, the total number of these is then (
.
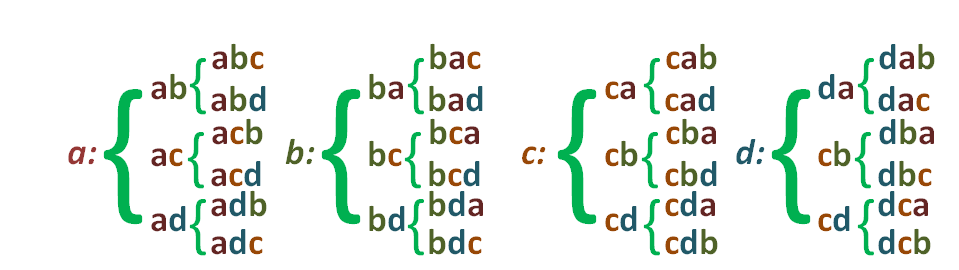
Finally the variations cuaternarias, or taken four to four, are deduced in a similar way and are all those ternary adding the last letter, so we will also get 24 variations.
From a general point of view we can say that the number of order variations n that can be formed with m elements (n <m) is obtained by multiplying those of order n-1 by the number of remaining elements, so this last number is given by the expression:
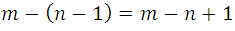
Symbolically and considering the expression for variations, the previous property can be expressed:
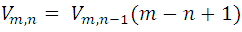
For example, the above expression is used as follows:
Now to calculate a variation 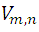we know that the number of variations of m elements taken one by one is m, in this way we can make use of:
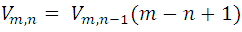
with n = 1,2,3, ..., n, successive you have to:
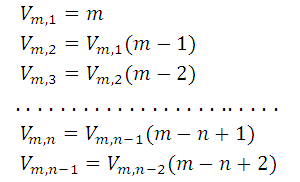
If we multiply these inequalities member by member, and simplify the common factors, it is clear to see:
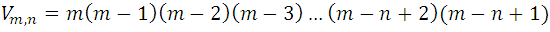
As this result is general, then:
The number
Then, as you can see, this is the formula for knowing the variations, for clarity let's denote an example:
- In a room where there are eight seats, five people enter, in how many ways can they sit?
The previous question clearly is a problem of variation because when changing the order of placement of people in the seats the groups are considered different. Then you have:
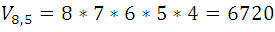
The previous number represents the numbers of how people can sit. Let's see another problem that deserves more algebra:
- If
, calculate the value of m
considering the expression of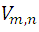 
for 
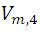and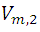 
we can write:
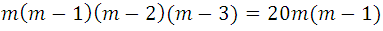
eliminating the common factors of both members, and we made the product:
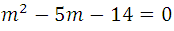
solving the second degree polynomial:
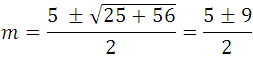
where do we get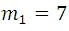 
, which is the value sought.
As you can see it is a very simple principle, but one that bases more complex mathematical operations, such as permutations and combinations, which also lead to a formula to calculate the coefficients of the newton polynomial, such concepts will be discussed later in the following post, I hope it is to your liking and benefit this humble. Thanks for reading and greetings to all.
References: