Hi, friends of steemit, I am going to make reference in this post about one of the most important man of the mathematical sciences, it is Pierre-Simon Laplace who was the precursor for the discovery of the mathematical maladies of laplace and the transformation of the equation that identifies it.

Pierre-Simon Laplace - the man who discovered and developed the Laplace transform and the Laplace equation

Astronomer, physicist and French mathematician (1749-1827)

Biography

Pierre-Simon Laplace (Beaumont-en-Auge, Normandy, France, March 28, 1749 -Paris, March 5, 1827) was a French astronomer, physicist and mathematician. Continuator of Newtonian mechanics, he discovered and developed the Laplace transform and the Laplace equation; as a statistician he laid the foundations of the analytical theory of probability; and as an astronomer he posed the nebular theory about the formation of the solar system. He shared the philosophical doctrine of scientific determinism.

Laplace strongly believed in causal determinism, as can be seen in the following quote:

We can look at the present state of the universe as the effect of the past and the cause of its future. One could conceive an intellect that at any given moment knew all the forces that animate the nature and positions of the beings that compose it; if this intellect were vast enough to subject the data to analysis, it could condense into a simple formula the movement of the great bodies of the universe and the lightest atom; for such an intellect nothing could be uncertain and the future, as well as the past, would be before their eyes.

This intellect refers to the demon of Laplace (cf. Maxwell's demon). The discoveries of modern physics, especially quantum mechanics and the uncertainty principle, prove that the existence of such an intellect is impossible at least in principle.

Laplace model

Its definition tells us that:

is E any experiment and S the finite set of its possible results such that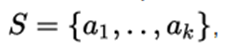

if we assume that each result is equiprobable (that none has more opportunities than another), then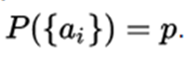

If we want P to be a probability function such that 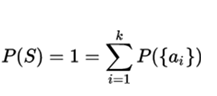so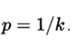

Let A be a subset of S such that 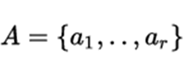then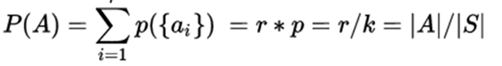

Transformations of Laplace

The Laplace transform is a type of integral transform frequently used for the resolution of ordinary differential equations. The Laplace transform of a function f (t) note defined for all positive numbers t ≥ 0, is the function.

Approximately in 1744, the Swiss mathematician Leonhard Euler, follower of the italofrancés Joseph-Louis de Lagrange, began to look for a solution for the differential equations in the form of:

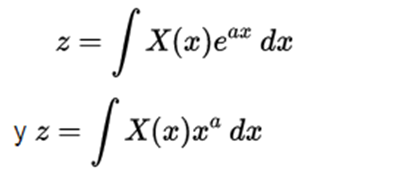
In 1785, Laplace found the next key, using integrals in the form of transformations of differential equations, which was simply the form of the solution, and found that the transformed equation was easy to solve, even more than the original.

References

1 . Etienne Le Gal / Lucien Klotz: We grands savants. Ce que tout Français doit en connaître. Delagrave, Paris 1926. Often also on March 23, 1749 is mentioned as date of birth, eg in: Jean François Eugène Robinet / Adolphe Robert / Julien Le Chaplain. Dictionnaire historique et biographique de la révolution et de l'empire. 1789-1815. 2 vols. Paris [1898].
2 . History of Probability and Statistics VI. José María ARRIBAS MACHO, Alejandro ALMAZÁN LLORENTE, Beatriz MAÑAS RAMÍREZ, Antonio Félix VALLEJOS IZQUIERDO. Editorial UNED, July 27, 2012 (Page 311)
3 . J. Bergasa, Laplace: the mathematician of the heavens, 2003, p.38

Bibliography

• Bergasa, Javier (2003). Laplace: the mathematician of the heavens. Nivola
• Simmons, J. (1996). The giant book of scientists - The 100 greatest minds of all time. Sydney: The Book Company.