Sequences: Functions with fantastic properties – Some known sequences: Arithmetic Progressions
Hello dear friends Steemians! Giving continuity to the series of posts about the fantastic successions, in the present I will talk about most well-known sequences, the so-called arithmetic progressions, its main properties and also, about one of the stories related to them, which has become in a legend in the field of Mathematics, and which involves one of the most prolific mathematicians of all time, the German Carl Friedrich Gauss (1777 - 1855).
Definition of an Arithmetic Sequence – Recurrence equation
An arithmetic progression or an arithmetic sequence is a sequence such that "the difference between any two consecutive terms is constant" [1], that is, one in which any term is equal to the previous one plus a constant called difference of the progression or simply difference. In other words, in the arithmetic progressions, each term is obtained from the previous one adding the constant quantity called difference.
For the arithmetic progression whose terms are:
It is true that: 
, 
, and in general:
where: 
is the difference (constant) of the progression, 
is the nth term or any of the sequence, and 
is the previous term to the nth term.
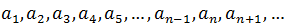
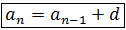
The previous expression, which is the recurrence formula of an arithmetic progression, shows that each term of the same is obtained from the previous one, adding the difference of the sequence. It is also common to rewrite it as:
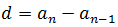
Some examples of arithmetic progressions are:
Example 1: The sequence of natural numbers:
whose difference is 1 (it is observed that when subtracting two consecutive terms the result is always 1).
Example 2: The sequence of positive integers multiples of 5:
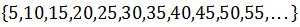
whose difference is 5 (it is observed that when subtracting two consecutive terms the result is always 5).
General term of an Arithmetic Progression
Using the recurrence formula of an arithmetic progression, all the terms of the sequence can be written, starting from the first term and knowing the difference, in the following way:
Generalizing, you get the formula of the nth or general term of an arithmetic progression:
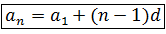
This formula allows obtaining any term of an arithmetic sequence known the first and the difference, without needing to know the preceding terms.
Example 3: What is the twentieth term of the sequence of positive integers multiples of 5?
The information provided by the given statement is:
Data
Solution
When replacing the data given in the formula of the general term, we obtain:
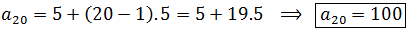
Sum of the first terms of an Arithmetic Progression
The sum of the first n terms of an arithmetic progression is written, using the sigma notation for the summation, as:
For a large number of terms, calculating such a sum is somewhat tedious, as it seemed to the child Gauss (read the anecdote below), but an equation can be obtained that speeds up such calculation (obtained by the child Gauss for the case of the progression of positive integers, although there is evidence that such formula "is known, at least, since the eighth century" [2]), rewriting the formula of the sum as follows:
where each term has been expressed in terms of the first and the difference using the formula of the general term.
Now, the terms are reordered in descending order (in terms of the index), obtaining:
Adding term to term the last two expressions, you get:
that is, the sum of n equal terms, which can be written as:
or as:
Using the formula of the general term again, we finally get the formula for the sum of the first n terms of an arithmetic progression:
Example 4: The sum of the first 100 positive integers (corresponding to the anecdote of the child Gauss and the progression of the positive integers), is obtained with 
, 
, 
:
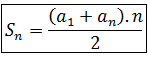
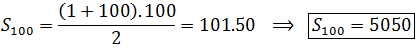
Gauss and the sum of the terms of an Arithmetic Progression: Amazing anecdote of a child prodigy
Is well known the anecdote of the child Gauss, known as the Prince of Mathematics, with respect to obtaining the formula (or rather its use?) of the sum of the first terms of the sequence of positive integers, although It is not clear if the story so really happened or has been added to the legend by his biographers.
In 1786, Gauss at the age of 9, in his first arithmetic class at the school where he was already two years old, his teacher J. B. Büttner proposed him, and his classmates, to add the first 100 positive integers, and Gauss found the answer almost instantly.
According to Brian Hayes, who compiled 109 versions of the famous anecdote, it happened like this:
"J. B. Büttner, teacher of a german school, punished all children by ordering them to add the first 100 natural numbers to keep them entertained and quiet for a while. Carl Friedrich Gauss got the answer almost immediately: 1 + 2 + 3 + ... + 99 + 100 = 5050." [2][3]
According to some of the versions compiled by Hayes, the child Gauss realized that the sum of the first and last term is 101 (1 + 100), that of the second and the penultimate is 101 (2 + 99), and that the sum of the equidistant terms of the sequence are all 101, so it had 50 addends equal to 101, with the result requested the product 101.50 = 5050. [3][4]
The supposed reasoning followed by Gauss leads to another demonstration of the formula of the sum of the first terms of an arithmetic sequence, different from the one shown above. In the case of a sequence with an even number of terms, the sum of its terms, adding the equidistant terms, is given by:
But:
And in general:
Where you get:
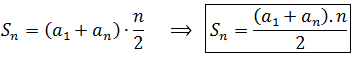
which is the same expression obtained previously using different reasoning.
Note: The equations were written in the Word equation editor. the figure 1 was obtained by editing the original in Paint.
Sources cited:
[1] Arithmetic Progressions – Wikipedia.
[2] The truth about the anecdote of Gauss – the child prodigy.
[3] Hayes, Brian, 2006. Gauss’s Day of Reckoning. A famous story about the boy wonder of mathematics has taken on a life of its own. American Scientitst, 94: 200, May-June.
[4] Carl Friedrich Gauss – Wikipedia.
Sources consulted:
[5] Fundación Polar, 2004. El Mundo de la Matemática. Fascículo 2. Sucesiones. Caracas: Últimas Noticias.
[6] Santillana, S.A. 2008. Matemática Primer Año (Programa de articulación). Cavelibro, Caracas.
[7] Navarro, Enrique. 1990. Matemática 1. Editorial Santillana, S.A. Caracas.
[8] Larson, Ron y Edwards, Bruce. 2010. Cálculo de una variable. Novena edición. McGraw-Hill/Interamericana Editores, S.A. México.
[9] Stewart, James. 2012. Cálculo de una variable. Séptima edición. Cengage Learning Editores, S.A. México.
I hope the post was of your interest and pleasure. If you have any question or suggestion, I invite you to leave your comment and I will gladly answer. Thanks for your kind reading.
Then, if it is of interest, I leave the link to the previous post of the series:
Sequences: Functions with fantastic properties – An Introduction.
In the next installment, I will talk about another of the most well-known sequences, the geometric progressions.
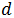
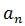
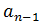
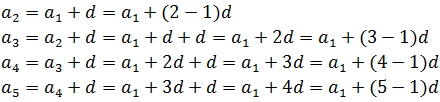
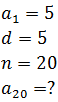
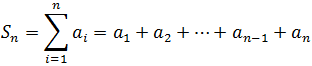
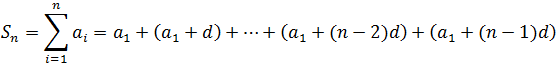
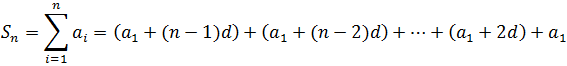
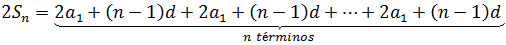
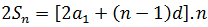
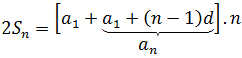
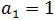
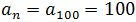
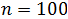
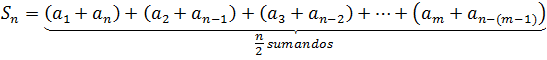
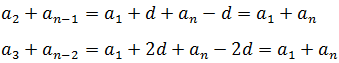
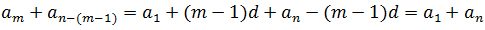
@OriginalWorks
The @OriginalWorks bot has determined this post by @hugobohor to be original material and upvoted it!
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!