Locus

Good day Steemians,I trust you all had a great weekend, and happy new week, may this week be full of great accomplishments.

I made this post by using my handphone, through esteem application by @good-karma. and all the images in the show is the result of a screenshot, from microsoft office power point.
Today, I'm going to tell you about locus, and some Example of locus.

What is Locus?

Definition
A locus is the path traced out by points that satisfy given conditions.

Example
The tip of minute hand of a clock moves between 12 noon and 1:00p.m. 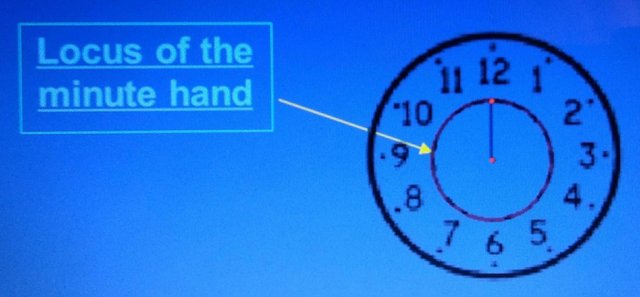The locus of the minute hand is a circle.

A football being kicked by a player. The locus of the ball is a curve.

A drop of water from tap. 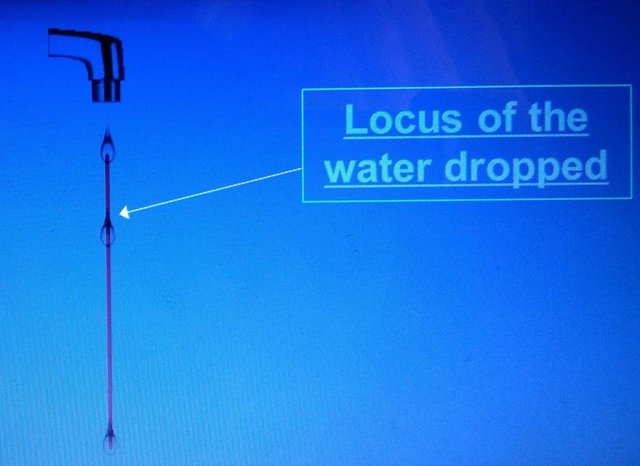The locus of the water dropped is a vertical straight line.

Somebody is standing on a moving up escalator. 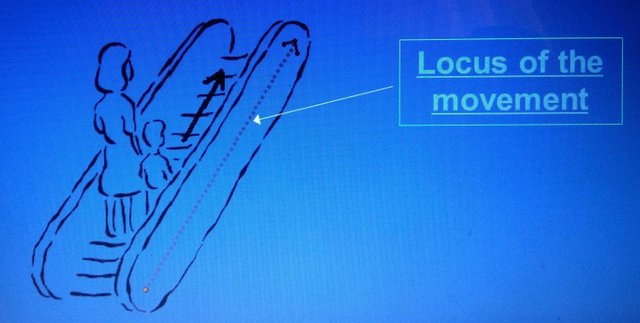The locus of the movement is a slanting straight line.

Determining and Constructing The Locus of A Moving Point.

Construction of Locus.
The locus of a moving point can be constructed using a ruler, a pair of compasses and a set square.

Determine The Locus of A Moving Point For 4 Conditions:

Locus of a moving point that is of constant distant from a fix point.

Locus of a moving point that is equidistant from two fixed points.

Locus of a moving point that is of constant distant from a straight line.

Locus of a moving point that is equidistant from two intersecting lines.

***. A point P moves in such a way that it is always x cm from a fixed point O. 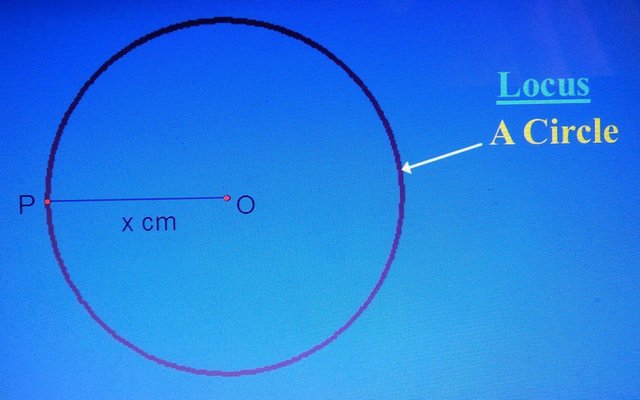The locus of a moving point that is of constant distant from a fix point is a circle.

Example
ABCD is a rectangle with sides 8cm and 10cm. Given BC is longer than AB, construct the locus of points that are
a. 2.5 cm from point A.
b. 2.0 cm from point B.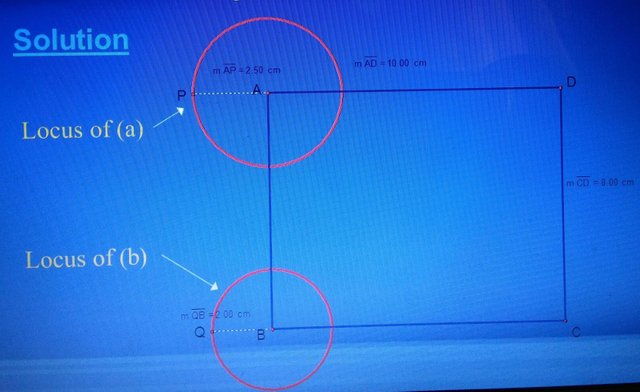

Example
The chair on the Ferris wheel rotates in a clockwise direction.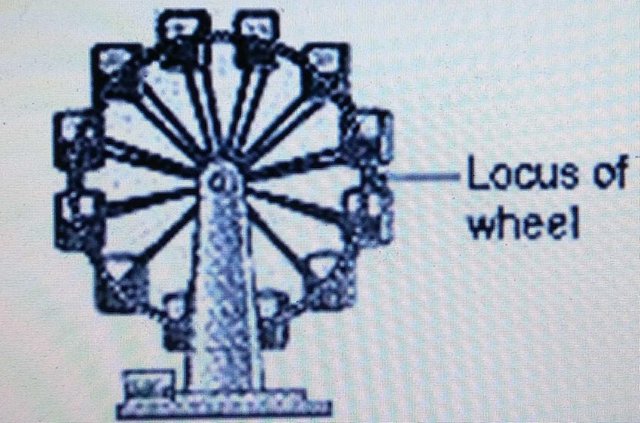

***. A point Q moves so that it is equidistant from two fixed points, A and B. 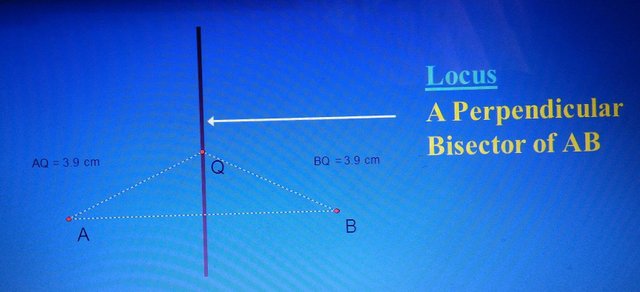The locus of a moving point that is equidistant from two fixed points is a perpendicular bisector.
Example
ABC is an isosceles triangle with sides 7 cm, 7 cm and 8 cm respectively. Given AB = AC. Construct the locus of points that are equidistant from
a. B and C b. A and B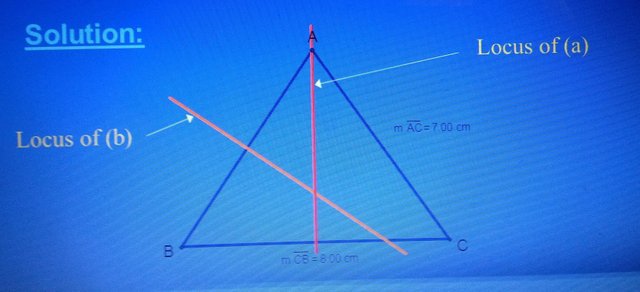

Example
The captain of a ship ensures that the ship is always equidistant from two islands. This is because the sea is deepest in between the islands.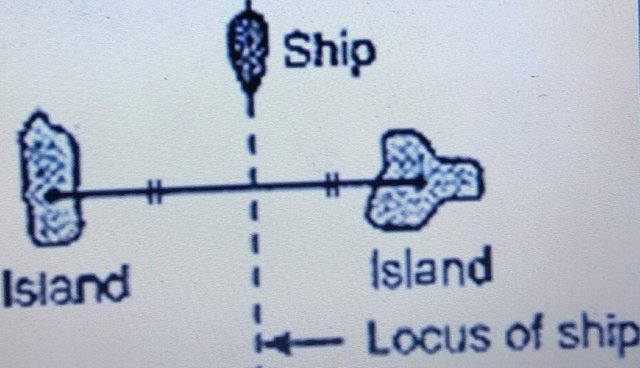

***. A point R moves in such a way that it is always x cm from a straight line MN. 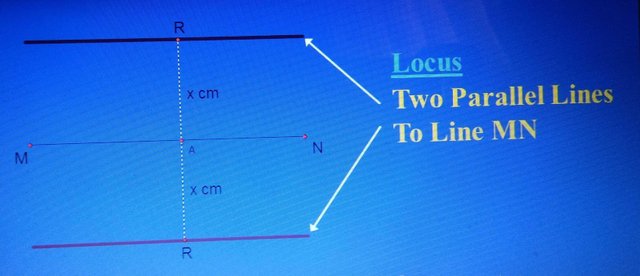The locus of a moving point that is of constant distant from a straight line is two parallel lines to the straight line.

Example
AB and BC are two perpendicular lines with lengths 5 cm and 6 cm respectively. Construct the loci of points that are
a. 1 cm from AB b. 2 cm from BC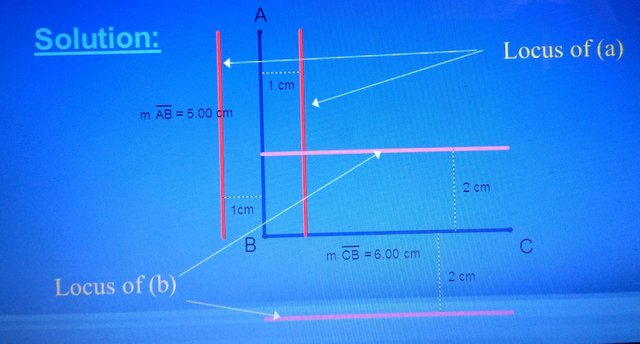

Example
A boy running parallel to fence.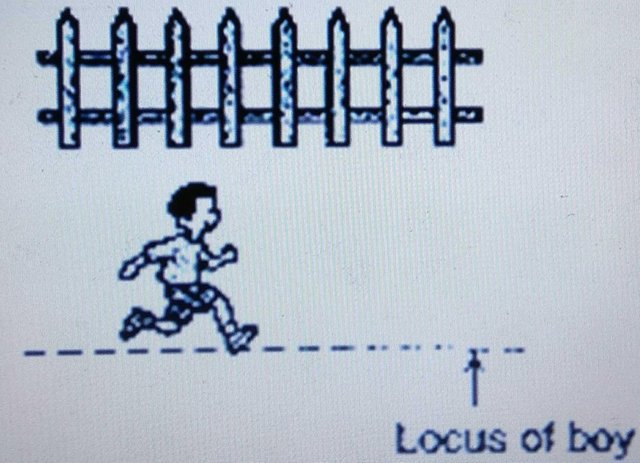

***. A point S moves in such a way that it is equidistant from two intersecting lines, L1 and L2. The locus of a moving point that is equidistant from two intersecting lines is an angle bisector.

Example
ABC is a right-angled triangle with sides 6 cm, 8cm and 10 cm respectively. Given angle ABC = 90 degree and BC is longer than AB, construct the locus of points which lie in the triangle that are equidistant from
a. AB and AC b. AB and BC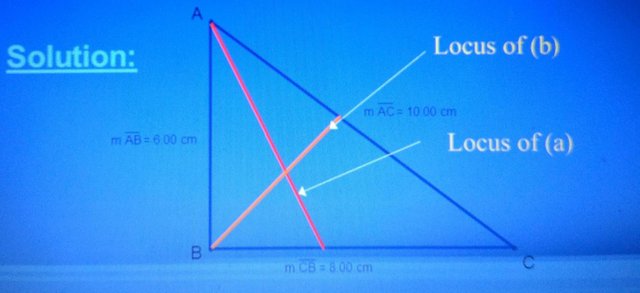

Example
A lizard crawls on the ceiling so that it is equidistant from two adjoining walls.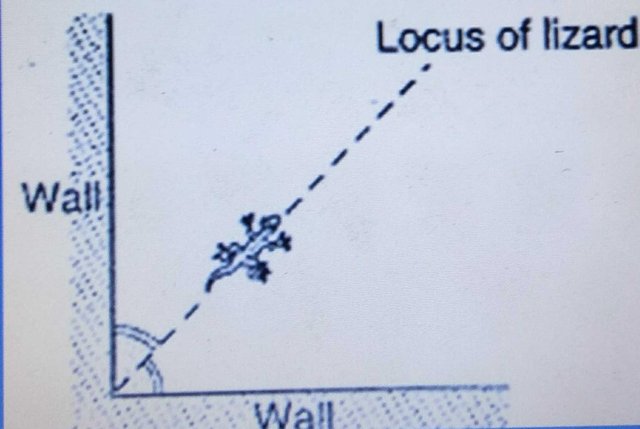

INTERSECTION OF TWO LOCI.

Determine The Intersection Of Two Loci.
When two loci intersect at a point P, then point P satisfies the conditions of two loci simultaneously.

Example
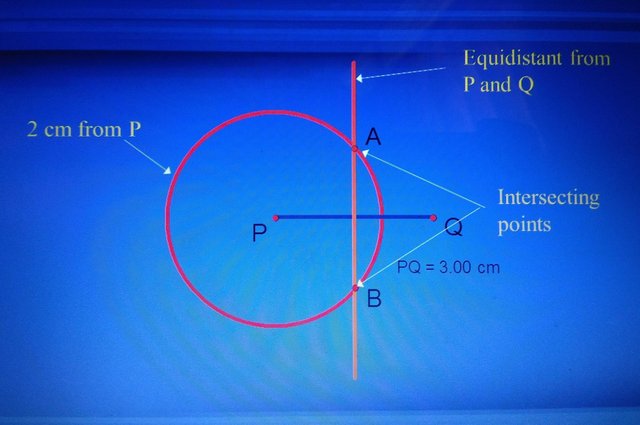
PQ is straight line of length 3 cm. Mark the points A and B that are 2 cm from P and equidistant from P and Q.

Solution

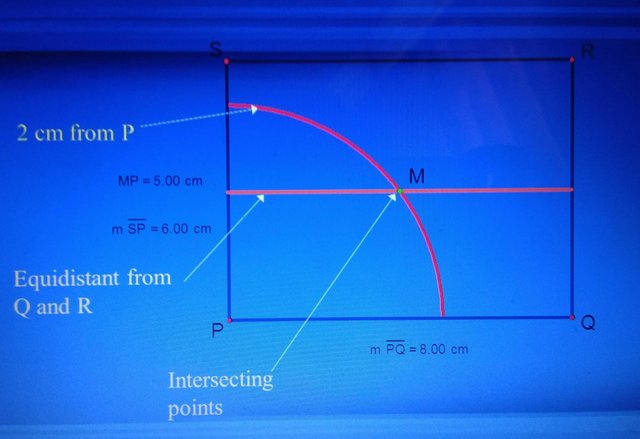
PQRS is a rectangle with sides 6 cm and 8 cm respectively. Given PQ is longer than QR. Mark the point M in the rectangle which satisfies the conditions
a. 5 cm from P
b. equidistant from Q and R.

Solution

EQUATION OF LOCI

An ant moves on the table ABCD so that it is always 2 cm from AB. Let AB be x-axis and AD be y-axis with scale 1 cm represent 1 unit. Found that the path of the ant moved is 2 cm from x-axis. So that, the path can be represented with equation y = 2. The path is called locus and y = 2 is equation of locus.

Equation of Locus Formation
The locus for a point moves so that it is always r cm from a fixed point.
The locus for a point moves in such a way that its distance from two fixed points is in a ratio given.

***. The locus for a point moves so that it is always r cm from a fixed point.
Example:
Find the equation of locus for a point P (x, y) moves in such a way that it is always 3cm from a fixed point A (1, -2).

1. What are you asked to find?
   Equation of locus
2. What information that you have?
   Distance P from A(1, -2) is 3 units,
   that is, AP = 3
3. How to solve it?
   Using the distance formula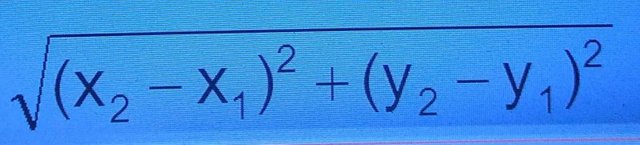
   Solution:
   P (x, y), A (1, -2), AP = 3
   Equation of locus :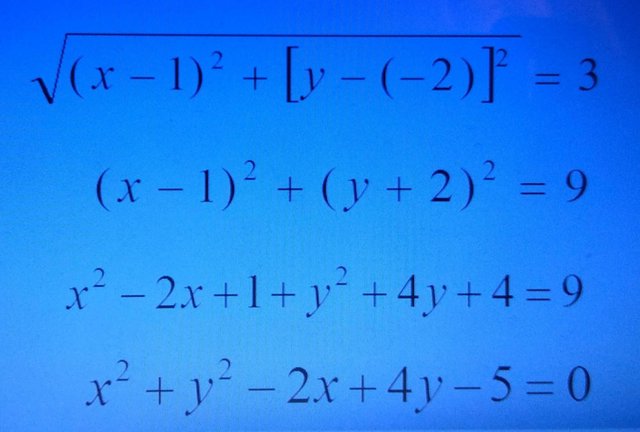

***. The locus for a point moves in such a
way that its distance from two fixed points is in a ratio given.
Example:
Find the equation of locus for a point Q (x, y) moves in such a way that the ratio of distance for point Q from two fixed point A (5, 1) and B (2, 4) is 2:1.

Solution:
Q (x, y), A (5, 1), B (2, 4), AP : BP = 2 : 1
Equation of locus :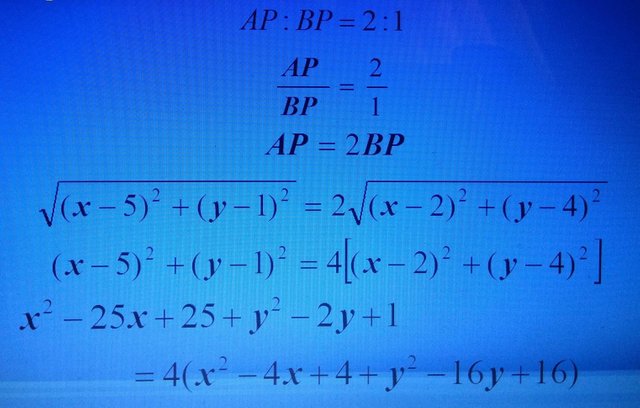

Hopefully this information is useful and can be promoted by @steemstem

BEST REGARDS @hhusaini