Digital Electronics Series - Mathematical Operations with Binary Numbers
Building Devices With Logic Gates - Part 2
In my last article, I talked about how digital electronics is at the heart of all computing systems. Computers read and write in 1s and 0s. I also talked about the different digital gates and how they process electrical signals. In part 2, we will see how the different mathematical operations such as addition can be done with binary numbers. We'll use our knowledge of the logic gates and try to link it with the methods of computation. This finally leads us to the point where we can actually use different gates to create logic circuits, which can do really cool stuff like add numbers and so on.
Mathematical Operations with Binary Numbers
Addition of Binary Numbers
There are four basic sums to remember for adding binary numbers. These are quite intuitive and can be deduced easily if we convert the number s from binary to decimal. The four sums are
0 + 0 = 0
This should be easy. 0 x 20 + 0 x 20 = 0
1 + 0 = 1
This follows, as 1 x 20 + 0 x 20 = 1
0 + 1 = 1
This condition is identical as the previous one.
1 + 1 = 10
Now this can be a little tricky. As we know, 1 x 20 + 1 x 20 = 2 (21). We get a 10 in binary. So what we do is we write the 0 in the digit place and write the 1 as a carry over.
Now one thing to notice is that, the table of the numbers in the results is 0,1,1,0 and 1 as carry. This looks familiar doesn't it? Yep, the numbers for the sum is identical to the truth table of a XOR gate. The carry, 1 is the result of the numbers (or signals) going through an AND gate.
Example - Adding two binary numbers
Lets take a simple example.
We know that 5 + 7 = 12
Now in binary, 5 is 101 and 7 is 111
How do you add 5 and 7 in binary?
We write down the numbers in the binary format.
1 + 1 = 10, so we write the sum as 0 and carry the 1.
1 + 0 + 1 is also equal to 10. Write the sum as 0 and carry the 1.
Now for the last sum, 1 + 1 + 1 = 11, or 3 in decimal. write the final sum to complete the addition and we got our final answer as 1100.
Now if you try converting 1100 to decimal, we get the decimal number 12.
We originally converted 5 and 7 to binary and added them to get their sum, 12 in binary format. How cool is that!
Now I had mentioned the XOR gate and the AND gate while we saw the results of adding binary bits. The same binary addition that we did by hand easily with logic circuits. Circuits called the half adder and the full adder are used for this. They are used everywhere, from computers to calculators, to process data. In the next article, I will explain how the half and full adders works and I will demonstrate how to make them with the chips I showed in the first article. Stay tuned for the next article!
The Digital Electronics Series
Part 1 : https://steemit.com/steemstem/@filler/digital-electronics-series-basics-of-logic-gates
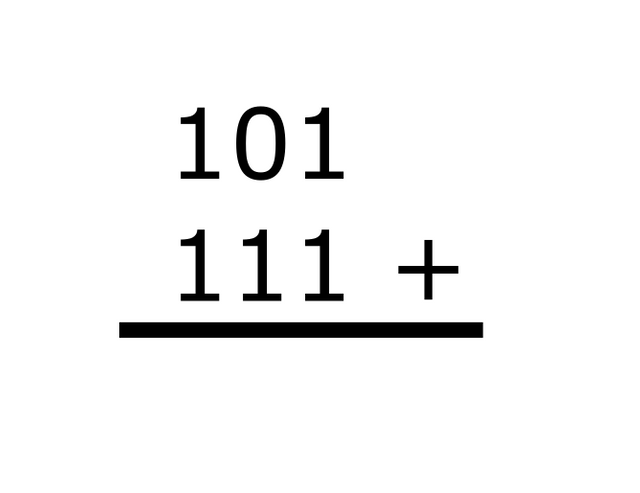
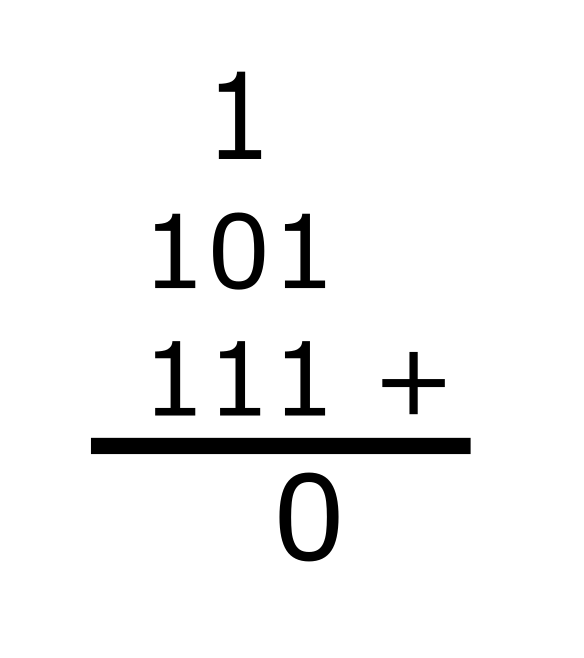
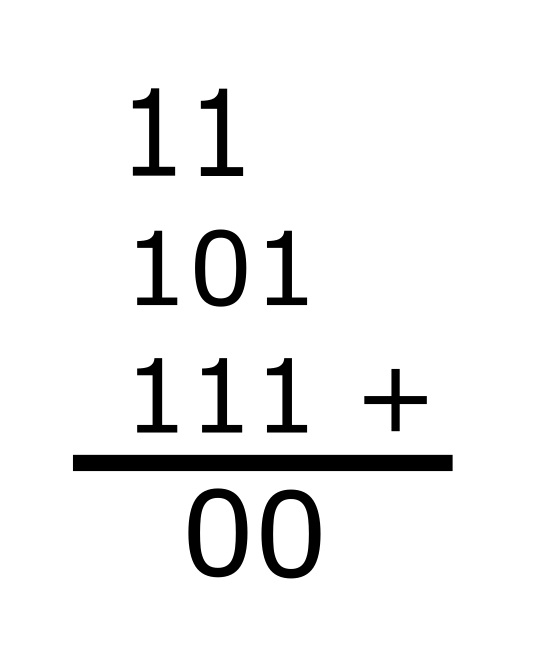
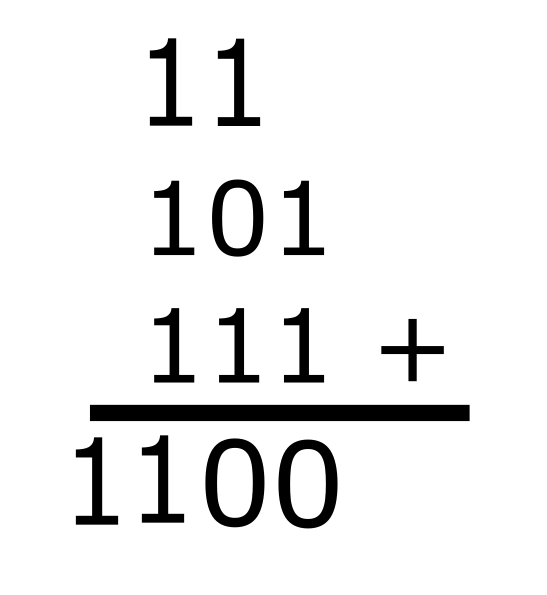
Nice one....this article is rich in knowledge.
a little above my head but I love all the educational content available on Steemit!