Rocket Science: Reaching Supersonic Speed with Design
Hey steemians, this is what I learned in class today. Thought I'd share my notes with you. I found this quite interesting. The variation of Pressure with the Mach number and how it dictates the flow in a CD-Nozzle
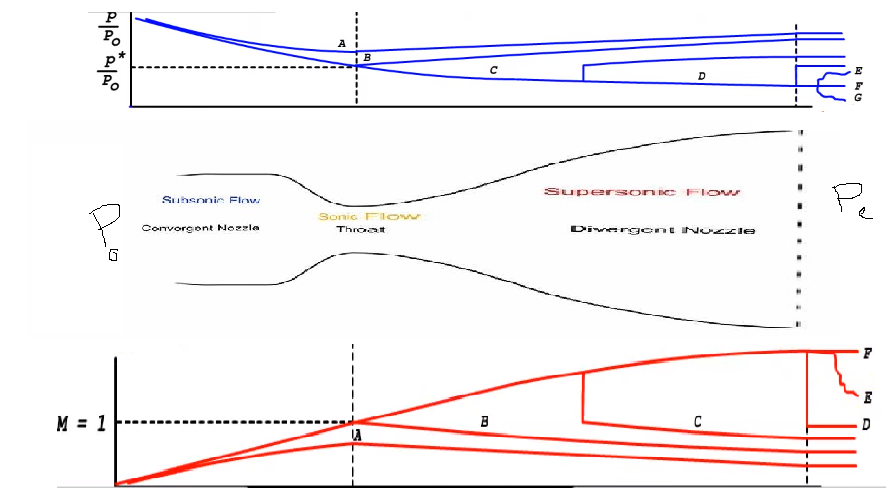
The figure is a representation of the variation of both Pressure ratio and Mach number along the length of the Converging- Diverging nozzle. The variation is caused due to the gradual reduction of outlet pressure which in turn causes the change in the mass flow rate and velocity of the gas.
For a gas flow with Mach number M<0.3 we consider it to be incompressible where we cannot reach a supersonic speed for the gas.
But as we drop the exit pressure gradually, further increasing the Mach number, we observe various cases of flow:
For M=0.7(A): The flow though no longer incompressible, still is at only a subsonic flow where the gas flow in both the converging portion and the diverging portion is sub sonic. This means the flow does not reach a supersonic state.
For M=1 at throat:
For M=1(B): Upon decreasing the exit pressure even further, we reach a crucial state where the flow speed of the gas at throat is equal to the speed of sound. The flow is similar to that of the first condition where the flow at both converging and diverging portions is subsonic but here we reach a special flow designation called “choked flow” because no matter how low the exit pressure is dropped at this point, the mass flow through the nozzle does not change.
The exit flow speed is not fast enough so this is not a desirable state for the magnitude of propulsion we desire.
For M>1(C): Now we try and decrease the exit pressure even below the exit pressure at choked flow with M=1. Here, the converging region still has a subsonic flow. But after the throat, the flow shows a strange behavior in a sense that even though the cross section increases after the throat, the flow velocity increases all the while the pressure increases. At this point, we reach supersonic speed in the nozzle for the first time. But since the pressure drop is not enough, shock waves will be created further along the cross section which will again render the flow subsonic.
Note: Here though we do not have an efficient system and do not remain at supersonic speed for a long time, we notice a pattern. We see that the further we decrease the exit pressure, we are able to reach supersonic speeds.
(D)Now we decrease the pressure at the outlet even further in such a way that the shock wave is created at the end of the nozzle exit. Though it may seem like a perfect nozzle, the flow after the nozzle will be subsonic since after supersonic pressure we have seen the flow is subsonic. So, we will need to decrease the pressure even further.
(E)Upon dropping the exit pressure further, the shock wave is created even further. It Causes shock wave after exiting nozzle with both supersonic and subsonic flows known as overextended flow. This is not optimum for our use.
(F) Finally upon decreasing the exit pressure to a point where the shock wave is created well behind the outlet of the nozzle we obtain the optimum range of working for the nozzle. It is logical that we dropped the optimal pressure at F and not E in a sense that most CD nozzles are used in rocket propulsion where they lift off and reach altitudes where the pressure decreases and reaches the right amount from E to F.
References
Farokhi, Saeed. Aircraft Propulsion. J. Wiley, 2014.