Con mis mejores deseos de bienestar y éxitos en el peregrinar de esta prestigiosa plataforma, especialmente a mis queridos amigos de Stem Español y Steemstem. En esta nueva oportunidad quiero explicarle el siguiente tema La Programación Lineal en la Identificación de Problemas en la Toma de Decisiones a continuación hago mención:

La programación lineal es una herramienta financiera que utiliza un modelo matemático para identificar los problemas y brindar ayuda en la toma de decisiones, es a través del procedimiento o algoritmo matemático que asigna eficientemente los recursos limitados, mediante el cual se resuelve un problema indeterminado, es decir optimizar una función lineal que se define como la función objetivo. Antes la vida solía ser mucho más simple de lo que es ahora, éramos capaces de detectar un problema, sugerir una solución, y después seguir adelante y hacer lo que se había decidido para resolver el problema. Anteriormente el mundo no era tan complicado y cuando la demanda de recursos financieros y humanos era muchísimo menor, hoy en día debemos ser en extremo cuidadosos a la hora de tomar decisiones, de manera que no se vayan a tomar acciones erradas o decisiones prematuras que nos cargue de más problemas.

Aunque bien intencionadas, muchas soluciones que la gente ofrece no están ligadas a fines importantes, y cuando los medios y los fines no están fuertemente ligados, a menudo fallamos, aun con las mejores intenciones. Estas son algunas causas de que en las últimas décadas se acuda a la programación lineal, ya que existen diversos mecanismos matemáticos que pudiesen solucionar los problemas derivados de las organizaciones. Es entonces, cuando se aplican estos métodos, que ayudan a reducir costos y maximizar ganancias.

INTRODUCCIÓN

Hoy en día la programación lineal es vista desde varios contextos. Sin embargo, la importancia no solo radica en el algoritmo matemático, para muchos es una parte integral de las matemáticas que nos permite utilizarla en cualquier organización, como una herramienta de soporte para la toma de decisiones. Con frecuencia la gente quiere vendernos su solución antes de lo que realmente sepamos cual es el problema. Las personas dicen que necesitan lujos, productos, programas o servicios, prácticamente todo aquello que no tienen. Podemos ahorrar dinero, tiempo y esfuerzo si identificamos claramente nuestros problemas antes de tomar decisiones. No son lo mismo necesidades que deseos ni tampoco problemas y soluciones. Por otro lado, las empresas le interesa producir más a un menor costo, se trazan metas u objetivos en común que deben alcanzar, es ahí donde la programación lineal nos dará la mejor opción.

Objetivo General:

Evaluar el modelo de la Programación Lineal en la Identificación de Problemas en la Toma de Decisiones.

Objetivos Específicos:

• Programar la función objetivo y las variables de Decisión en la Identificación del problema.

• Examinar cada una de las restricciones y la utilización del modelo de Programación Lineal para así poder acertar la cantidad óptima.

• Determinar los factores en los criterios que pueden afectar los resultados y el cálculo de una solución que maximice o minimice el resultado deseado.

• Identificar resultados deseados para los problemas de las empresas.

• Plantear las estrategias que se pueden utilizar para identificar los problemas y así encontrar soluciones alternativas y adecuadas en la toma de decisiones.

Con el paso del tiempo, y de los avances tecnológicos vivimos en un mundo más cambiante y cada vez más competitivo en el cual los mercados se ven en la necesidad de ser más eficientes y eficaces para mantenerse vigentes en el tiempo. De esta manera, el modelo de decisión de programación lineal puede ayudar a optimizar inmediatamente los recursos de la mejor manera y alcanzar mayores beneficios con ventajas competitivas y provecho de los recursos de la organización. Es evidente, que la programación lineal en la actualidad es aprovechada por muchas organizaciones, ya que es un método matemático realmente atractivo para los casos de análisis complicados, cuyos modelos implican estudiar el funcionamiento interno de la empresa como su estructura de producción.

Sin embargo, a menudo se observa que entre las diversas actividades que ocurre en las organizaciones, hay la existencia de actividades que compiten muchas veces por los recursos limitados que tienen la organización, es en ese espacio donde la programación lineal se desempeña como una herramienta importante para identificar el problema, en otras palabras la programación lineal es el proceso de planificar de la mejor forma un conjunto de actividades para alcanzar objetivos específicos evaluados para ellos, asignando de mejor manera los recursos limitados y aprenden a tomar decisiones, es el momento para ponderar alternativas, desechar lo que no sirve y saber seleccionar lo que en un momento determinado es útil y beneficioso para todo el equipo humano de las organizaciones.

Por otro lado, las características de las funciones del problema y de las variables tienen diferentes tipos de problemas de Programación Matemática. Si todas las funciones del problema, objetivo y restricciones son lineales, se tiene un problema de Programación Lineal, que conlleva a la solución óptima un programa de acción a poner en práctica. Este procedimiento utiliza varias variables como: La inversión que podemos tener, cantidad de mano de obra , los productos más vendidos, todo estos es lo que describimos como restricciones que opera en el método simples de la programación lineal para determinar si una empresa puede permanecer a corto o largo plazo en el mercado.

Como Inicialmente lo describimos, Un problema de Programación Lineal consiste en optimizar (maximizar o minimizar) la función:

Z = F ( x1, x2, ... ,xn ) = c1x1 + c2x2 + ... + cnxn

sujeto a:
a11x1 + a12x2 + . . . + a1nxn ≤ = ≥ b

a21x1 + a22x2 + . . . + a2nxn ≤ = ≥ b2

Am1x1 + amx2 + . . . + amnxn ≤ = ≥ bm

X1 , x2 , . . . , xn ≥ 0

Se le denomina función objetivo o Función criterio, a la función
= F(x1,x2....,Xn)=c1x1 + c2x2......+ cnxn

• Los coeficientes están representado por: c1, c2, ... , cn son números reales y se llaman coeficientes de beneficio o coeficientes de costo, Estos datos aparecen descritos en el problema.

• Las variables de decisión están conformada por x1, x2, ... , xn o niveles de actividad que deben establecerse.

• Las desigualdades ai1x1 + ai2x2 + . . . + ainxn ≤ bi , con i = 1, ... , m se llaman restricciones.

• Los coeficientes tecnológicos aij , con i = 1, ... , m y j = 1, ... , n son también números reales.

• Así mismo el vector del lado derecho, los términos bi , con i = 1, ... , m, se llama vector de disponibilidades o requerimientos y son datos conocidos e identificados en el problema.

• Por otro lado las restricciones xj ≥ 0 con j = 1, ... , n se exclaman como condiciones de no negatividad.

• A todas las restricciones se le denomina región factible que en el conjunto de valores de (x1, x2, ... ,xn) que satisfacen simultáneamente todas las restricciones.

Por otro lado, cuando hablamos de solución óptima es el punto de la región factible que hace máxima o mínima la función objetivo. En el estudio de un problema de Programación Lineal, es básico elegir las restricciones, se obtendrán escenarios diferentes, acotados o no, y según sea la posición de la función objetivo respecto de dicho escenario o poliedro se pueden originar diferentes situaciones. Según el tipo de soluciones que presenten un problema de Programación Lineal puede ser de acuerdo a si existe la región factible, en el cual se presentan varios casos:

• El Óptimo finito. La solución óptima está formada por un único punto con coordenadas reales.

• Los Múltiples óptimos. Un problema de Programación Lineal puede tener más de un óptimo.

• El Óptimo infinito. Es donde la función objetivo puede tomar, un valor tan grande o tan pequeño como se quiera sin desertar la región factible.

• Región factible no acotada, óptimo finito. La función objetivo alcance el óptimo en la zona acotada de la región factible.

• Región factible no acotada, óptimo finito e infinito. Se Obtiene el caso en que todos los puntos de una de las semirrectas que determinan la región factible no acotada sean solución del problema.

• No factible. Región factible vacía. El conjunto de restricciones de un problema puede ser incompatible, conduciendo a una región factible vacía.

Para resolver un problema de Programación Lineal tenemos que representar la región factible resolviendo el sistema de inecuaciones formado por el conjunto de restricciones. Para resolver un sistema de inecuaciones lineales tendremos que resolver cada una de las inecuaciones que lo forman y después encontrar la intersección de todos los semiplanos solución (región factible). Por otro lado, al momento de desarrollar problemas de Programación Lineal es importante conocer la descripción del Teorema que a continuación hago mención:

Teorema fundamental de la Programación lineal en la Identificación de Problemas en la Toma de Decisiones

Si un problema de Programación Lineal tiene región factible no vacía, entonces, si existe el óptimo (máximo o mínimo) de la función objetivo, se encuentra en un punto extremo (vértice) de la región factible. Si una función alcanza el valor óptimo en dos vértices consecutivos de la región factible, entonces alcanza también dicho valor óptimo en todos los puntos del segmento que determinan ambos vértices. Teniendo en cuenta el teorema anterior, para calcular el máximo o el mínimo de una función, será suficiente con evaluar la función objetivo en todos los vértices de la región factible y quedarnos con el que proporciona el valor óptimo

Caso Practico 1: Aplicaciones de la Programación Lineal en Problemas de Inversión para decidir cual genera la mayor Rentabilidad.

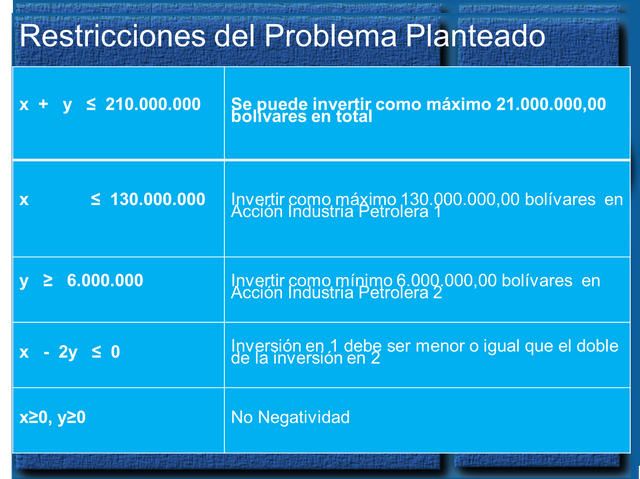
Un sr dispone de un capital de 210.000.000,00 bolívares para invertir en acciones de la industria petrolera. El gerente le recomienda dos acciones que han estado ofertando porque han estado en alza: Acción Industria Petrolera 1 y Acción Industria Petrolera II en el estado Anzoátegui. La 1 tiene una renta del 10% anual y la 2 del 8% anual. Su amigo le recomienda invertir en un máximo de 130.000.000,00 bolívares en la Acción 1 y como mínimo 6.000.000, 00 bolívares en la Acción 2. Además la inversión en la Acción 1 debe ser menor o igual que la inversión destinada a la Acción 2. Se quiere plantear y resolver un modelo de Programación Lineal que permita obtener la política de inversión que permita obtener la máxima rentabilidad anual.

1.- Describimos las Variables de Decisión:

X= Bolívares invertidos en la Industria Petrolera 1
Y= Bolívares invertidos en la Industria Petrolera 2

2.- Determinar la Función Objetivo:

Es Maximizar la Rentabilidad anual que resulta invertir en las acciones de las dos Industrias Petroleras.

Maximizar es 0,1x+0,08Y

Ahora procedemos a la Formula de Programación Lineal donde vamos a sustituir las variables:
La Solución Óptima:

F ( x1, x2, ... ,xn ) = c1x1 + c2x2 + ... + cnxn

X= 130.000.000,00

Y= 6.000.000,00

Donde Maximizar es: 0.1 x + 0,08 y

F(x,y)= 0,1 (130.000.000,00) + 0,08(6.000.000,00)

F(x,y)= 13.000.000,00+480.000,00

F(x,y)=13.480.000,00

Finalmente obtenemos el Valor Optimo= 13.480.000,00. Esta es donde se maximiza la rentabilidad anual de la Industria Petrolera de ambas acciones

En un proximo post daremos a continuación sobre este problema y el tema planteado.

Observación:

Las imágenes fueron realizadas en el Programa de Microsoft Power Point por mi autoría

Referencias:

• Gabaldón, Fernando. (2003) Técnicas de Negociación. Primera Edición. Editorial IMMECA.
• Gomollon, Felix (1996) Ejercicios de Investigación de Operaciones. Madrid. Editorial ESIC.
• Fedossova, Alina y Buitrago, Oscar. (2011). Introducción a la Programación Lineal con Administración de Operaciones. Bogotá. Editorial CESA.

Los invito a leer contenidos de ciencias, matemáticas, ingeniería, tecnología y salud visitando la etiqueta #Stem-espanol, a su vez unirse al canal de discord https://discord.gg/djk49A, donde los días jueves a las 8 pm Hora de Venezuela podrás participar en los conservatorios.

Lcda. Exqueila Rodriguez Diaz

Especialista en Derecho Mercantil Mención Talento Humano
Egresada de la Universidad de los Andes