Understanding the Effects of Forces in Structures and Micro-structures.
In 1940, a bridge was commissioned in Washington State in the US; the Tacoma Narrows Bridge. It was so unfortunate that the bridge had to collapse just after four months. It didn’t collapse because of the influence of an earthquake but for poor designing. The bridge wasn’t designed strong enough to withstand the forces of very strong winds.
When we talk of structures, we mostly think of the massive and breathtaking engineering constructions such as the [57km twin-bore Gotthard base tunnel](https://www.google.com/amp/s/www.bbc.com/news/amp/world-europe-36423250) that rail-link Switzerland to the rest of Northern and Southern Europe, or the longest suspension bridge in the world, the 6-lanes [Akashi Kaikyo](https://www.roadtraffic-technology.com/features/feature-the-worlds-longest-suspension-bridges/) bridge in Japan. Or, some might think of [BurjKhalifa](https://en.m.wikipedia.org/wiki/Burj_Khalifa) in Dubai (with a total height of 2,717 feet excluding the antenna) or one of the tallest buildings in the United States such as the [One World Trade Center](https://en.m.wikipedia.org/wiki/One_World_Trade_Center) (with a total height of 1,792 feet) and the tallest skyscraper in China, the [Shanghai Tower](https://www.thebalancesmb.com/shanghai-tower-china-s-tallest-skyscraper-844664) with over 2,073 feet in height.
All over the world, engineers and architects are challenging themselves on who to build the largest structure and the [Jeddah Tower](https://edition.cnn.com/style/amp/jeddah-tower-saudi-arabia-new/index.html), under construction in Saudi Arabia remains the tallest building in the world so far.
Big structures like bridges and buildings are mostly motionless while some move only to a very small degree in the wind. The structures are affected by very large force as a result of their own mass, and the ground on which they are erected. There must be a balance and stability in the force acting on these structures; they must counteract each other in every components and direction. In a situation whereby the forces on the structure do not balance out, then there would be some acceleration, which is in accordance with Newton’s second law. Newton said in his second law of motion that the acceleration of a body is directly proportional to the force on the body but inversely proportional to its mass (i.e **F=ma**).
 )
)
Resultant force
Source:[Ilevanat, Own work; CC BY-SA 3.0]( )
)
So, the study of forces that keep structures staying up without moving (i.e in equilibrium) is called statics. Forces can also be said to be in equilibrium when a body is moving uniformly in a straight line without accelerating. But to notice how forces act on a body, then we have to analyze all the forces that are acting on it. From high school physics, we were taught that a force is an example of a vector quantity because it has both magnitude and direction. And that there are many methods that can be adopted in adding two or more forces together. One of which is the **parallelogram method.**
To add two forces using the parallelogram method, we draw a parallelogram of forces as is shown in the illustration at the right hand side.
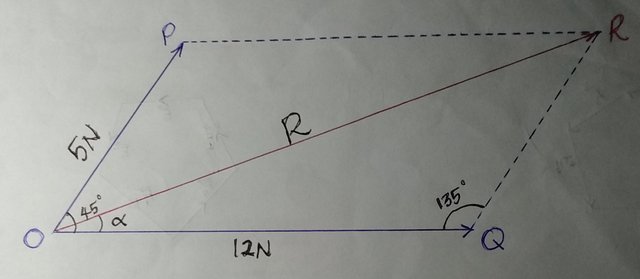
**To find the resultant of forces acting at angles greater or lesser than 90 degrees to each other. Let’s assume you are asked to find the resultant of two forces each of 5 Newtons and 12 Newtons respectively acting at an angle of 45° with each other.**
 )
)
An illustration drawn by me to show the resultant of two forces each of 5 Newtons and 12 Newtons respectively acting at an angle of 45° with each other.
**Using the analytical method: The resultant force can be determined analytically by using the [cosine rule](https://en.m.wikipedia.org/wiki/Law_of_cosines) and then the sine rule:**
#### (OR)2 = (OP)2 + (OQ)2– 2(OP)×(OQ)×cosθ
#### (OR)2 = 52 + 122 – 2 (5) × (12) × cos 135°
#### (OR)2 = 25 + 144 + (120 × 0.7071)
#### (OR)2 = 253.852
#### (OR) = (253.852)1/2
#### (OR) = 15.93 Newtons.
#### Using the [sine rule](https://en.m.wikipedia.org/wiki/Law_of_sines), we will get:
#### sinα/(QR) = sin(135°)/(OR) = 0.7071/(OR)
#### sinα = (12×0.7071)/15.93
#### α = (sin)-1 0.5327
#### α = 32.18°
The same approach applies if we are to calculate the resultant of the two forces acting at an angle greater than 90 degrees with each other. Usually, if two vectors A and B are inclined at θ° to each other, then the resultant vector R is given as: **R2 = A2 + B2 - 2(A)(B)cosθ**
**Using the scale drawing method: The resultant force can also be determined graphically by choosing an appropriate scale, then draw the forces (OP) and (OQ) to represent 5 Newtons and 12 Newtons at an angle of 45° with each other. Finish up the parallelogram by drawing (OR) parallel to (OP) and (QR). Join OR. So, OR represents the resultant force in magnitude and direction.**
#### To find the resultant of forces acting at right angles with each other.
**It is easier to calculate the resultant force when they act on an object at right angles with each other. Assume you are asked to determine the resultant of two forces 5 Newtons and 12 Newtons acting at a right angle.**
Coplanar forces mean several forces acting on a body on the same plane. Let’s assume there are three forces acting at a point. The effect of those three forces can be shown using three spring balances connected by strings to a particular point and with the opposite ends of the spring balance hooked to three fixed points as shown in the illustration below. The force in spring 3 must be equal and opposite to the resultant force of spring 1 and 2, as shown by the diagonal of the parallelogram. The same parallelogram can be drawn for the pair of springs 1 and 3 and also for the pair of springs 2 and 3. These resultants in their circumstance will be in equilibrium with the forces on springs 2 and 1 respectively.
 )
)
An illustration by me showing three forces in equilibrium
To find the general resultant force of coplanar forces, one can represent the forces by vectors drawn to a scale on a sheet of paper. We then take the forces in pair and draw parallelogram of forces for each pair and afterward get a resultant for each pair.
When the gravitational force on an object of determinate size is considered, it can be expected that this force acts through a single point inside that object. The resultant gravitational force of such a body can then be shown by a particular arrow which amounts to be the total sum of the forces on all areas of the object.
Building massive structures aren’t as easy as it looks, a lot of factors need to be taken cognizance of, which if neglected or overlooked, will affect the stability and durability of a structure. Very much also is understanding the type of materials needed for construction; materials that should be able to withstand the impact of force and other conditions so as not to jeopardize lives and properties. Past experience of building collapse has taught the modern day engineers to rigorously test their structures at every stage of construction before they can be ascertained to be safe enough for use. In the same vein, we need to understand statics, a type of force that keeps structures in equilibrium. Furthermore, a force - product of a mass of a body and its acceleration- is a quantity with magnitude and direction which can be resolved in different ways. The resultant force can then be determined by either using the parallelogram method, analytical or scale drawing. Understanding the concept of a point object, the centre of mass and gravity and how several forces act on a body all go a long way in constructing one of the massive structures in the world.
All in all, there are still many more effects of forces on structures, an example of which is the type of forces acting on a radio mast, forces not meeting at a point (non-coplanar), moments of force, like in a tower crane. So, also is the types of forces an engineer need to consider in the construction of a suspension bridge, all which I hope to write about in my next post. But, till then, I remain my humble self, @emperorhassy
## Thanks for reading.
 )
)
 )
)
##
 )
)
The Leaning Tower of Pisa
Source:[Pixabay, JimboChan; CC0](https://pixabay.com/photos/pisa-leaning-tower-unintended-tilt-1056568/)
Also in the construction of the Leaning Tower of Pisa in Italy, the eight-stories tower was built on a soil which was unstable enough to withstand the large structure. The tower started to tilt right from when the construction was on the third level and beyond. It got to a stage that the building started to sink and afterwards began to rotate, till the situation was later salvaged by the engineers.
So, the need to comprehend how materials behave when they are forced to undergo some impact cannot be over-emphasized because it is precisely a case of life and death. Engineers and builders have come to realize that they don’t need to depend on theory alone when building great structures but to pay attention to even the minutest of details. Past experience has taught them to test their designs on prototypes faultless to the smallest detail before they start to erect structures. Then further tests are carried out at each of the stages throughout the course of construction.
These tests at times can be very impressive. Taking for instance, in the building of the suspension bridge in Tokyo, the Japanese had to drop onto the middle of the bridge, a very heavy hammer weighing up to 100 tonnes at a height of 60 metres. The resulting impact caused ripples of waves along the bridge, distorted it and made it twist like a corkscrew. It was only because the bridge was able to withstand such an amount of huge force that it was considered safe enough for use.
 )
)
 )
)
The Burj Khalifah building in Dubai
Source:[Pixabay, Didiwo; CC0](https://pixabay.com/photos/burj-khalifa-building-dubai-city-1096446/)
 )
)
So, what is the concept behind constructing structures?
When we talk of structures, we mostly think of the massive and breathtaking engineering constructions such as the [57km twin-bore Gotthard base tunnel](https://www.google.com/amp/s/www.bbc.com/news/amp/world-europe-36423250) that rail-link Switzerland to the rest of Northern and Southern Europe, or the longest suspension bridge in the world, the 6-lanes [Akashi Kaikyo](https://www.roadtraffic-technology.com/features/feature-the-worlds-longest-suspension-bridges/) bridge in Japan. Or, some might think of [BurjKhalifa](https://en.m.wikipedia.org/wiki/Burj_Khalifa) in Dubai (with a total height of 2,717 feet excluding the antenna) or one of the tallest buildings in the United States such as the [One World Trade Center](https://en.m.wikipedia.org/wiki/One_World_Trade_Center) (with a total height of 1,792 feet) and the tallest skyscraper in China, the [Shanghai Tower](https://www.thebalancesmb.com/shanghai-tower-china-s-tallest-skyscraper-844664) with over 2,073 feet in height.
All over the world, engineers and architects are challenging themselves on who to build the largest structure and the [Jeddah Tower](https://edition.cnn.com/style/amp/jeddah-tower-saudi-arabia-new/index.html), under construction in Saudi Arabia remains the tallest building in the world so far.
 )
)
The latest rendering of the newly green-lighted Kingdom Tower in Jeddah, Saudi Arabia.
Source:[Forbes.com,Kerryadolan; CC0]( )
)
The concepts behind the toughness and strength of these awe-inspiring structures, and the forces influencing them, also relate on a much smaller size to plates, racks and the smallest of materials. So, I will be talking more on these forces, and also on the properties of the materials used in the structures, since we know that all materials originated from separate atoms. I will also expatiate more on how the properties of different materials emerge from their atomic and molecular arrangements and also on the combination of the atoms and molecules to make up a microstructure.
 )
)
 )
)How do structures stay up?
Big structures like bridges and buildings are mostly motionless while some move only to a very small degree in the wind. The structures are affected by very large force as a result of their own mass, and the ground on which they are erected. There must be a balance and stability in the force acting on these structures; they must counteract each other in every components and direction. In a situation whereby the forces on the structure do not balance out, then there would be some acceleration, which is in accordance with Newton’s second law. Newton said in his second law of motion that the acceleration of a body is directly proportional to the force on the body but inversely proportional to its mass (i.e **F=ma**).
 )
)
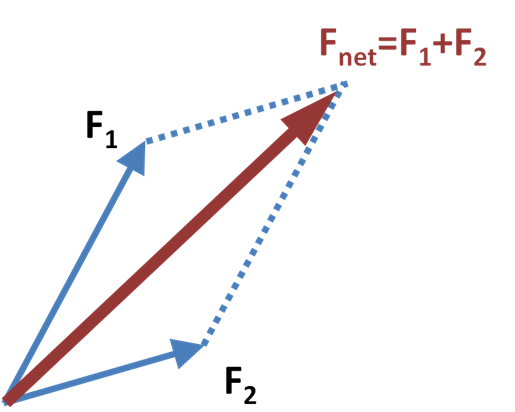
The Parallelogram method
To add two forces using the parallelogram method, we draw a parallelogram of forces as is shown in the illustration at the right hand side.
 )
)
Parallelogram of vectors
Author:[Brews ohare, Own work; CC BY-SA 3.0]( )
)
The **resultant** of the two forces is represented by the diagonal of the parallelogram with the two forces as adjacent sides. The magnitude and direction of the resultant force can then be determined either through calculations or by scale drawing. A resultant force is that single force that would have the same effect in magnitude and direction as the original forces acting together.
 )
)
To determine the resultant of forces both analytically and graphically
**To find the resultant of forces acting at angles greater or lesser than 90 degrees to each other. Let’s assume you are asked to find the resultant of two forces each of 5 Newtons and 12 Newtons respectively acting at an angle of 45° with each other.**
 )
)
 )
)
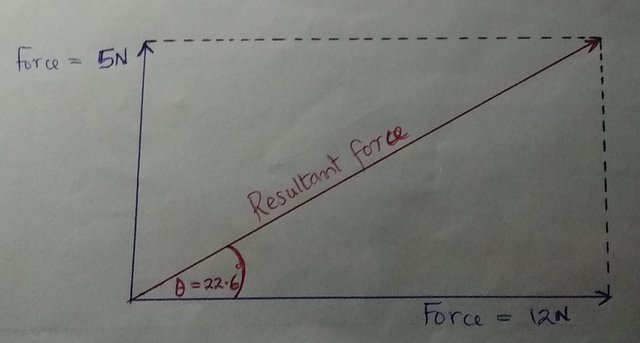
An illustration drawn by me to show the resultant of two forces each of 5 Newtons and 12 Newtons respectively acting at an angle of 90° with each other.
**Using the analytical method:** The magnitude and direction of the resultant force can be calculated by using trigonometry. So, using **[Pythagoras’ theorem:](https://en.wikipedia.org/wiki/Pythagorean_theorem)**
#### (resultant force)2 = (5)2 + (12)2 = 169
#### resultant force = √169 = 13 Newtons.
#### The angle θ between the resultant and the 12 N force has a tangent equal to 5/12:
#### θ = (tan)-1 (5/12)
#### θ = 22.6°
**Using the scale drawing method: Draw to scale the forces acting at a point on the object. Ensure the two forces are drawn acting at a single point. In this case, the parallelogram is completed since it’s a rectangle. Finally, the diagonal of the parallelogram is drawn by starting from the point at which the forces act. This diagonal represents the resultant force.**
 )
)
Coplanar forces acting at a point
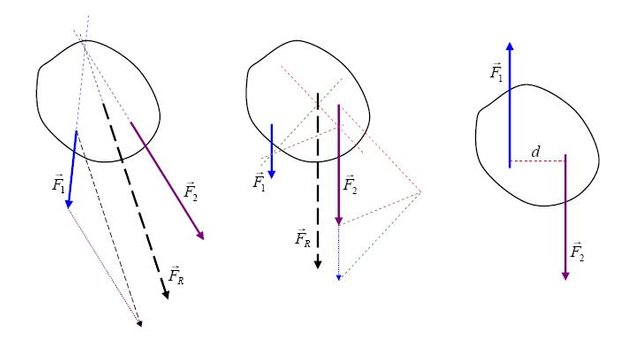
Coplanar forces mean several forces acting on a body on the same plane. Let’s assume there are three forces acting at a point. The effect of those three forces can be shown using three spring balances connected by strings to a particular point and with the opposite ends of the spring balance hooked to three fixed points as shown in the illustration below. The force in spring 3 must be equal and opposite to the resultant force of spring 1 and 2, as shown by the diagonal of the parallelogram. The same parallelogram can be drawn for the pair of springs 1 and 3 and also for the pair of springs 2 and 3. These resultants in their circumstance will be in equilibrium with the forces on springs 2 and 1 respectively.
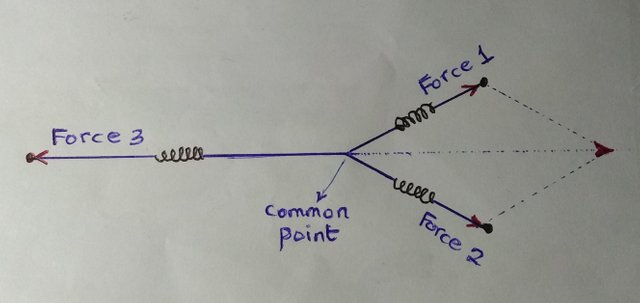 )
)
 )
)
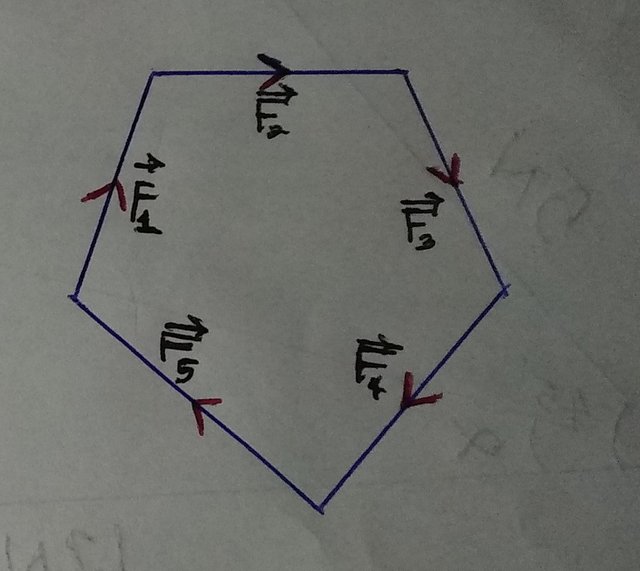
(Five forces forming a closed polygon. If these five forces act at a single point within a body, they will be in equilibrium and thus provide no acceleration on the body.)
We can pair up these resultants and redo the process until we are now left with one overall resultant force. But one thing that’s noticed is that this method can be time wasting when we have a lot of forces to contend with.
We could also extend to forces in three-dimensions, and then resolve in the x, y, and z directions. But even for 3D buildings and structures, it’s the two-dimensional cross-section that’s mostly considered. So, I won’t muddle up my analysis in this segment with the third dimension.
So, talking about forces acting in a single x-y plane, so far the forces act through a **single point** in a body and the body isn’t accelerating, then the resultant force must be zero. The forces can be drawn as vectors and we then add up the vectors tail-to-head one after the other. For a body undergoing zero resultant force, the vectors will form the sides of a closed polygon as is shown in the first illustration above.
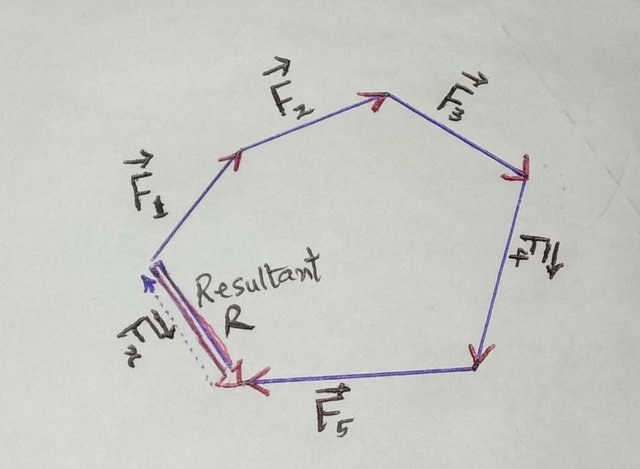
But, if the vectors do not close up, then the line Fx that connects the polygon indicates both the magnitude and direction of the additional force needed for equilibrium as illustrated below.
 )
)
 )
)
(Five forces not in equilibrium. Resultant force R is in the opposite direction to the force needed to close the polygon i.e to achieve equilibrium.)
But, in the absence of this extra vector force, the resultant force R on the body will be equal and opposite in direction and thus produce acceleration on the body. A point object is an object that is very small to an extent that all the forces acting on it are considered to be meeting at a point. Most times, the forces acting on a larger body all converge at the centre of mass, thereby enabling us to consider a large body as equivalent to a single point. Conclusively, it can be stated that any point object that is acted upon by a number of forces will in equilibrium if and only if the force vectors form a closed polygon.
I wouldn’t conclude this post without talking about the centre of gravity; it’s one of the most important effects of force on massive and microstructures.
 )
)
Centre of Gravity
When the gravitational force on an object of determinate size is considered, it can be expected that this force acts through a single point inside that object. The resultant gravitational force of such a body can then be shown by a particular arrow which amounts to be the total sum of the forces on all areas of the object.
 )
)
A bird's toy displays the scientific principle of center of gravity.
(Source:[Own work, Author: APN MJM; CC BY-SA 3.0)]( )
)
Hence, the centre of gravity is that point through which all weight is seen to act. But, for day-to-day activities on earth, the centre of gravity is also regarded as the centre of mass. It is that point through which an exerted force does not make the object to rotate. It is easy to locate the centre of mass and the centre of gravity for symmetrical (i.e regular) object of uniform weight unlike the irregular object. In an asymmetrical (i.e irregular) flat object, the centre of gravity can be located by hanging the object freely from two or more different positions very close to its edge.
 )
)
 )
)Conclusion
Building massive structures aren’t as easy as it looks, a lot of factors need to be taken cognizance of, which if neglected or overlooked, will affect the stability and durability of a structure. Very much also is understanding the type of materials needed for construction; materials that should be able to withstand the impact of force and other conditions so as not to jeopardize lives and properties. Past experience of building collapse has taught the modern day engineers to rigorously test their structures at every stage of construction before they can be ascertained to be safe enough for use. In the same vein, we need to understand statics, a type of force that keeps structures in equilibrium. Furthermore, a force - product of a mass of a body and its acceleration- is a quantity with magnitude and direction which can be resolved in different ways. The resultant force can then be determined by either using the parallelogram method, analytical or scale drawing. Understanding the concept of a point object, the centre of mass and gravity and how several forces act on a body all go a long way in constructing one of the massive structures in the world.
All in all, there are still many more effects of forces on structures, an example of which is the type of forces acting on a radio mast, forces not meeting at a point (non-coplanar), moments of force, like in a tower crane. So, also is the types of forces an engineer need to consider in the construction of a suspension bridge, all which I hope to write about in my next post. But, till then, I remain my humble self, @emperorhassy
## Thanks for reading.
 )
)
REFERENCES
[Top ten largest construction projects](https://www.thebalancesmb.com/top-ten-largest-construction-projects-844370) [How Engineering bridges handle stress](https://bridgemastersinc.com/engineering-bridges-handle-stress/) [Effects of force on structures](https://www.questia.com/library/journal/1G1-93089425/the-effects-of-force-on-a-structure-strength-and) [Forces That Can Act on Structures - Wrdsb pdf](https://www.google.com/url?sa=t&source=web&rct=j&url=http://teachers.wrdsb.ca/goodacre/files/2014/03/sci7_unit_b_sec04-02.pdf&ved=2ahUKEwiohtCYvPTgAhX1URUIHTwuDFAQFjABegQIDhAE&usg=AOvVaw2R2JGr-y7JWmhsSGLCj7ci) [Structures and forces pdf](https://www.google.com/url?sa=t&source=web&rct=j&url=http://www.edquest.ca/pdf/sia74-2notes.pdf&ved=2ahUKEwiohtCYvPTgAhX1URUIHTwuDFAQFjAUegQIBhAB&usg=AOvVaw1dQmV6zSI6_oTINZBX3vuQ&cshid=1552114499013) [57km twin-bore Gotthard base tunnel](https://www.google.com/amp/s/www.bbc.com/news/amp/world-europe-36423250) [Jeddah Tower](https://edition.cnn.com/style/amp/jeddah-tower-saudi-arabia-new/index.html) [Akashi Kaikyo](https://www.roadtraffic-technology.com/features/feature-the-worlds-longest-suspension-bridges/) [BurjKhalifa](https://en.m.wikipedia.org/wiki/Burj_Khalifa) [One World Trade Center](https://en.m.wikipedia.org/wiki/One_World_Trade_Center) [Shanghai Tower](https://www.thebalancesmb.com/shanghai-tower-china-s-tallest-skyscraper-844664) New School Physics by Dr M.W Ayankoha, Scalars and Vectors, Book 2 Chapt. 1; pg 115 Collins Physics By Collins educational, Materials and forces, Chapt. 5; pg 32  )
)
 )

 )
)
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Congratulations @emperorhassy! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPHi @emperorhassy!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV