THE LAWS OF THERMODYNAMICS: Obtaining the Lowest Temperature in the World.

By this stage of physics, we will have spent a lot of time learning about properties of materials – conductors have resistance, fluids are viscous, and so on. But at very low temperatures we cannot take these properties for granted. At 4 K, for example, mercury loses all its electrical resistance and so can carry a current forever without any reduction in the current. At very low temperatures, helium becomes a fluid that loses its viscosity and can flow freely. Oxygen even becomes magnetic.

Scientists are working to achieve lower and lower temperatures and trying to discover more unusual low-temperature properties in a wider range of materials.

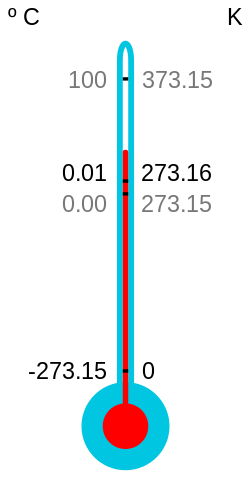
The absolute zero of temperature has been defined as 0 K (about -273.16 °C), when the only remaining energy is ‘zero-point’ energy that arises from the so-called uncertainty principle and can never be removed. We also know that we will never be able to reach absolute zero. But that doesn’t stop scientists from trying to get as close to it as possible.

Eric A. Cornell, Wolfgang Ketterle and Carl E. Wieman of the United States shared the 2001 Nobel Prize for Physics for research that involved cooling a gas down to just above 1 nK (1 billionth of a degree above absolute zero). The technique involved slowing down alkali atoms by colliding photons head-on with them and then skimming off the faster atoms by evaporative cooling to obtain a condensate. But competition continues. At the low-temperature Laboratory in Helsinki, Finland, a piece of rhodium metal has since been cooled to 100 pk (0.1 nk).

The ideas in this chapter

Ever since physicists knew about absolute zero temperature, they have been trying to reach it. This is a problem of thermodynamics, that is, the study of energy transfer processes including work and heating, and how these two processes are connected.

But thermodynamics is a lot more than trying to reach absolute zero. Thermodynamics explains why we can heat and expand a gas to drive internal combustion engines: most vehicles rely on some form of thermodynamic (heat) engine. It explains the limits to transferring energy, and shows, for example, that we can never build a totally efficient power station to supply electricity. In the home, thermodynamics explains the operation of refrigerators and other equipment that we use to do work for us.

THE ZEROTH LAW

When physicists first began to study thermodynamics, they identified three laws. Logically enough, they called these laws the first, second and third laws of thermodynamics. However, in the 1930s they realised that there was a much more fundamental law than these, so, rather than change the names of the others, they called the new one the zeroth law of thermodynamics.

This states: If two bodies are in thermal equilibrium with a third body, then they must be in thermal equilibrium with each other.

If two or more bodies are in this kind of equilibrium, they must have the same temperature because thermal energy is not transferred between bodies that are at the same temperature. For energy to be transferred thermally, a temperature gradient is required. Without the zeroth law a practical thermometer would not be possible.

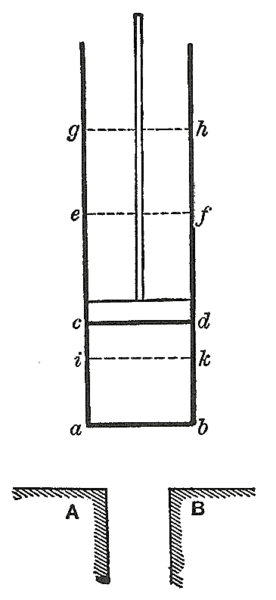
We use the zeroth law in calibrating a thermometer. A practical thermometer (such as a mercury thermometer) and a gas thermometer are both placed in a liquid or similar reservoir of thermal energy. The gas thermometer is an ‘ideal’ thermometer used to define temperature. Both thermometers reach thermal equilibrium with the liquid. Then the two thermometers are also in equilibrium with each other and so they are at the same temperature. This means that the practical thermometer can be calibrated against the gas thermometer for a fixed temperature. Further points can be established by altering the temperature of the liquid as measured using the gas thermometer.

^{Carnot engine diagram (modern) - where an amount of heat QH flows from a high temperature TH furnace through the fluid of the "working body" (working substance) and the remaining heat QC flows into the cold sink TC, thus forcing the working substance to do mechanical work W on the surroundings, via cycles of contractions and expansions. Eric Gaba Public Domain}

THE FIRST LAW

We saw that Joule found he could increase the temperature of water by doing work on it. He kept the water thermally insulated from the surroundings so that no energy was thermally transmitted to the water from outside. But the internal energy of the water changed. The internal energy is the sum of the potential and kinetic energy of the molecules in the substance. We use the symbol U for internal energy (measured in joules) and represent a small change by ΔU. We assume that a small amount of work ΔW is done to produce this change of internal energy. So the change of internal energy in joules is:

ΔU = ΔW

Alternatively, the internal energy of the water could be increased by allowing energy to enter from the outside, usually by thermal processes (such as conduction). We often call this energy ‘heat’ or ‘thermal energy’. Assume that this amount of energy (in joules) entering the water is small, represented by ΔQ. The change of internal energy is given by:

ΔU = ΔQ

This assumes no work has been done.

But most changes in the internal energy of a body arise from a combination of both thermal transfer and mechanical transfer of energy or work. So more generally, we write:

ΔU = ΔQ + ΔW

We can use any combination of amounts of thermal energy or mechanical energy (work) to produce a given change of internal energy ΔU. The equation is an algebraic statement of the first law of thermodynamics. We can state the law in words: The increase in internal energy of a system is the sum of the work done on the system and the energy supplied thermally to the system.

It is probably easier for us to remember the law as the equation ΔU = ΔQ + ΔW. Notice that in words, the law refers to a system. In our example, the system is the mass of water whose temperature has been raised by work or heating.

Sometimes we need to consider what happens to more than one object: we may have to consider the behaviour of a number of components. We refer to them altogether as our system – we can think of the system as surrounded by an imaginary wall. All things outside this wall are the surroundings. The system plus its surroundings taken together make up its universe.

Although energy can be transformed in different ways, it is not possible to create or destroy energy. Later, I will discuss about how mass can be turned into energy and how energy can be transformed into mass. This is possible only with nuclear interactions; it does not happen in everyday thermodynamics.

APPLYING THE FIRST LAW TO A GAS

Most real-life engines contain a gas which is heated and expands, and the gas (which does the work) follows a cycle of changes before it ends up under the same set of conditions as when it started the cycle. I shall look at the expansion of a gas, and other changes, restricting ourselves to an ideal gas. Because there are no forces of attraction or repulsion between the molecules of an ideal gas, the only way that the internal energy and the temperature of the gas can change is to change the kinetic energy of the molecules. This, in turn, makes an ideal gas system easier to consider than many of other systems.

We look at what happens when work is done by the gas. Let's assume that the gas is inside a cylinder with one of its end closed. And, at the other end is a piston. The molecules travel round inside the cylinder, having a collision with the walls, and rebounding off the walls and piston. This causes a pressure p on the walls and piston. The pressure acts on the piston of area A, producing an overall force:

F = pA

Suppose that, as a result of this force, the piston moves outwards slightly so that the volume of the gas increases. We then make the following assumptions:

• There is neglectable friction between the walls of the cylinder and the piston.
• The force F that is exerted by the gas is balanced by an external force F.
• But the external force will be reduced by a very minute amount.

This very slight imbalance of forces allows the piston to move. We assume it travels a small distance Δx so that there is negligible change of pressure of the gas. The volume of the gas changes by a small amount ΔV. The gas does work ΔW in expanding against the external force. We therefore have:

work = force × distance

ΔW = FΔx = pAΔx

The product AΔx is the increase in volume ΔV of the gas. So the work done by the gas is:

ΔW = pΔV

Note that if we consider the work done on the gas, the equation must have a minus sign:

ΔW = -pΔV

EXAMPLE

A circular piston of diameter 40 mm contains a gas at 3 atmospheres. Calculate the work done by the gas when the piston moves outwards a small distance (compared with the length of the cylinder) of 5 mm. Given that 1 atmosphere = 1.01 × 10⁵ Pa.

Answer: Work done = pressure × change of volume

= pAΔx

= 3 × 1.01 × 10⁵ × [π × (20 × 10^-3)² × 5 × 10^-3] J = 1.9 J

ISOTHERMAL CHANGES IN A GAS

When the volume of a sample of gas changes, there is often a change of pressure. A common situation is for a gas to change its volume at constant temperature, that is, under isothermal conditions. Here we can use the equation of state for an ideal gas:

pV = nRT

where R is the gas constant and n is the number of moles in the sample. Experimentally, we can achieve an isothermal change by changing the volume slowly so that the gas remains in thermal equilibrium (that is at the same temperature) with the surroundings. With temperature constant, the pressure is related to volume by:

p = constant/v

This inverse dependence is shown on the pV diagram. To find the work done by the gas when it expands, we plot the curve for actual values of p and V and measure the area under the curve. Remember: work done = pAV. We measure the area by adding up the areas of the large number of strips (each a pΔV) making up the total area. Alternatively, we can obtain a mathematical expression for the work done. This does not require values of p to be calculated.

Calculation of the work done by a gas during an isothermal expansion

For a small change in volume, the work done is given by:

ΔW = pΔV                            [1]

Also we use the ideal gas equation:

p =nRT/V

Substituting for p from equation 1

We get:

ΔW = nRTΔV/V

Instead of adding strips of width ΔV, we use calculus to integrate dW = nRTdV/V between the initial volume V₁ and the final volume V₂:

dW = ∫nRTdV/v = nRT∫dV/V

As the integral of dV/V is In V, we obtain:

dW = nRT[ln V] = nRT(In V₂ – InV₁) = nRT In (V₂/V₁)

CHANGE OF PRESSURE OF A GAS AT CONSTANT VOLUME

Rather than changing the volume of a gas at constant pressure, we might choose to alter the pressure at constant volume. Suppose the gas is in a container with fixed walls and we change the temperature by either heating or cooling. Because the volume is fixed, the gas equation tells us we can expect the pressure to rise with a temperature increase: the kinetic energy of the gas molecules increases, their momentum increases, they make greater impacts as they collide with the walls, and so pressure on the walls increases.

Although we change the internal energy, no work is done. We can confirm this on the pV diagram where the change is represented by a vertical line: below this line there is no area.

How much energy is required to raise the temperature of the gas by 1 kelvin? The amount will depend on the quantity of gas involved. We usually take one mole of gas and quote the molar heat capacity, which is the amount of energy in Joules required to heat 1 mole by 1 kelvin. The symbol for this is C_v.

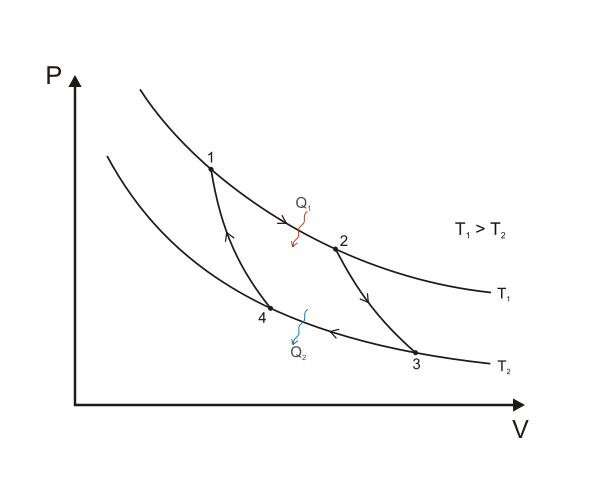
^{A Carnot cycle illustrated on a PV diagram to illustrate the work done. Keta, CC BY-SA 3.0}

The amount of energy needed to increase the temperature of the gas by a small amount ΔT is C_vΔT. The subscript V tells us that this is the molar heat capacity at constant volume. No work is done on the gas (it does not change volume). All the thermal energy Q_v supplied goes to changing the internal energy of the gas. For 1 mole of gas:

ΔU = ΔQ_v + C_vΔT

CHANGE OF VOLUME OFA GAS AT CONSTANT PRESSURE

We have seen that the work done by an ideal gas in expanding by a small amount ΔV is pΔV. If the expansion is large, the only way in which the pressure can remain constant (from the gas equation) is for the temperature to increase. The pV diagram tells us that work done is still pressure × volume change, as this is the area under the horizontal line representing the change.

Again, we need to be able to work out by how much internal energy is increased. This time, we use the molar heat capacity at constant pressure, C_p. It is defined as the amount of energy in joules required to heat 1 mole of gas by 1 kelvin at constant pressure. For gases, the molar heat capacities at constant pressure and constant volume are not the same. When an ideal gas is heated at constant pressure its volume increases. It must do work against its surroundings as well as increase its internal energy (kinetic energy of the molecules). As a result, we expect the molar heat capacity at constant pressure to be significantly larger than that for constant volume for a gas. For liquids and solids, the difference is very small because they expand very little on heating at constant pressure.

SUMMARY OF MOLAR HEAT CAPACITIES FOR AN IDEAL GAS

Assume that Q_v is the thermal energy which is joined to the ideal gas at constant volume, Q_p is the thermal energy that is added at constant pressure, and ΔT is the change in temperature in each case. Then, for n moles of the gas:

ΔQ_v = nC_vΔT and ΔQ_p = nC_pΔT

that is:

C_v = ΔQ_v/nΔT and C_v = ΔQ_v/nΔT

It can be shown that there is a simple relationship between the two molar heat capacities for an ideal gas: C_p – C_v = R

REFERENCES

https://www.coursehero.com/file/p393hja/The-reference-gas-thermometer-C-is-in-thermal-equilibrium-with-liquid-B/

https://www.livescience.com/29913-coldest-places-on-earth.html

https://en.wikipedia.org/wiki/List_of_weather_records

https://en.wikipedia.org/wiki/Lowest_temperature_recorded_on_Earth

https://www.thoughtco.com/zeroth-law-of-thermodynamics-4177952

https://courses.lumenlearning.com/boundless-physics/chapter/the-zeroth-law-of-thermodynamics/

https://www.livescience.com/50833-zeroth-law-thermodynamics.html

https://en.wikipedia.org/wiki/Zeroth_law_of_thermodynamics

https://www.britannica.com/science/thermodynamics/The-first-law-of-thermodynamics

https://www.livescience.com/50881-first-law-thermodynamics.html

https://en.wikipedia.org/wiki/First_law_of_thermodynamics

http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/isoth.html

https://www.askiitians.com/iit-jee-thermal-physics/work-done-during-isothermal-expansion.html

https://en.wikipedia.org/wiki/Isothermal_process

https://www.youtube.com/watch?v=m9h6qyWLscs

https://www.khanacademy.org/science/chemistry/thermodynamics-chemistry/internal-energy-sal/a/pressure-volume-work

https://www.bbc.co.uk/bitesize/guides/zc4xsbk/revision/3

http://chemistry.bd.psu.edu/jircitano/gases.html

https://www.grc.nasa.gov/www/k-12/Numbers/Math/Mathematical_Thinking/ideal_gases_under_constant.htm

https://opentextbc.ca/chemistry/chapter/9-2-relating-pressure-volume-amount-and-temperature-the-ideal-gas-law/

https://en.wikipedia.org/wiki/Gas_laws