Let B be the matrix associated to the Arnold map, so B =[1 1;1 2] . Then with some effort you can show that B^48 mod 576 is equal to the identity matrix. This explains the result.
So you can write B as B=invXDX where X is the eigen matrix with corresponding eigenvalues on the diagonal of the diagonal matrix D. It is then easy compute B^m you then need to find an m such that B^m mod size of your matrix is equal to the identity matrix. So this gives you equations to find the periodicity
When you iterate you only have to compute D^m D is a diagonal matrix so that is pretty easy to compute. X and invX stay the same. More specifically B^m=invX D^m X
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Do you have by any chance examples of practical applications of this kind of maps? Thanks!
PS: I love the cat output :D
I just saw that this transform is applied to encrypt images. Attaching the researchgate link to a related publication: https://www.researchgate.net/publication/309463059_Arnold's_Cat_Map_Algorithm_in_Digital_Image_Encryption
I am yet to see other applications in real world.
Thanks! Don't hesitate to share anything you could you hear about future applications of this.
Okay 😃
Thank you😻.
Reminds me of my old TV. ;-)
We used to call those noise patterns as grains 😂
What is the size of the matrix s for your cat jpg? I am guessing that it has just the right size for periodicity to occur.
Posted using Partiko Android
the original size was 576x640. But for simplicity of coding, I resized it to 576x576.
that is a right guess. there are some bounds for this periodicity. From https://arxiv.org/pdf/1111.2984.pdf
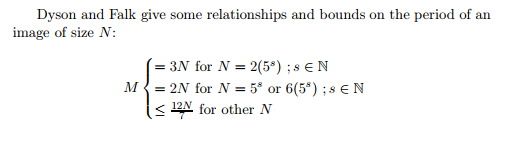
And some samples:
Let B be the matrix associated to the Arnold map, so B =[1 1;1 2] . Then with some effort you can show that B^48 mod 576 is equal to the identity matrix. This explains the result.
Posted using Partiko Android
Oh ok. That is a nice find. But is there a general rule to find periodicity of any number sized image?
So you can write B as B=invXDX where X is the eigen matrix with corresponding eigenvalues on the diagonal of the diagonal matrix D. It is then easy compute B^m you then need to find an m such that B^m mod size of your matrix is equal to the identity matrix. So this gives you equations to find the periodicity
Posted using Partiko Android
Again to find m I will have to iterate till I see identity matrix right? So that means it is sometimes computationally intensive right?
When you iterate you only have to compute D^m D is a diagonal matrix so that is pretty easy to compute. X and invX stay the same. More specifically B^m=invX D^m X
Posted using Partiko Android
Ah so I guess it is 576. 576=48x12. Probably there is some kind of reason for this.
Posted using Partiko Android
Hi @dexterdev!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV