The function of the Linear and constant, identity in the science of Mathematics
 Source Image : Google
Source Image : GoogleIn the function, there are several important terms, which include :
Domain is the region of origin of the function (F) denoted with (Df).
The kodomain is the area of comrade, function (F) denoted with (Kf).
Range, i.e., the region of result which is the subset of the kodomain. The range of functions (F) is denoted with (Rf).
Now we understood with the function definition in mathematics. Let's look at more on the subject of this function, which includes, properties, types and examples of questions and answers.
Nature of the functions in the Math
Now let's see what are the properties of functions in mathematics.
1. Injection function
The nature of the first function is injektif or also called function one-one. Literally, we may not yet understand clearly. To more easily understand the nature of this function, I give an example to you. For example the function (F) states (A) to (B) then the function (F) called a function one-one (injektif), When each of the two different elements in (A) will be mapped on two different elements in (B).
2. The function of Surjektif
The function of (F: A) → (B) is called to function or function surjectively, And if for any (B) in kodomain (B) there is at least one (A) in domain (A) so that apply (F(A) = (B). In other words, a kodomain surjektif function the same with the (range).
3. The function of Bijektif
The nature of the function of the last mathematics is bijektif. A mapping (F: A)→(B) in such a way that (F) was a function injektif. And surjektif at once, then "(F) is the function that bijektif" or " (A) and (B) located in correspondence one-one.
The types of the function of Mathematics
After we know the nature of the function, let us see what types of mathematic function?
below this :
1. Linear Function
The first type is linear. The functions on the real numbers is defined : (F(X) = (AX) (B), (A) and (B) constant with (A) ≠ (0) called linear function.
2. The constant function
For more easier for you to understand the type of the second function, I give an example. E.g. (F:A)→(B) is a function in the (A) then the function (F) called constant. and if the coverage from (F) only consists of one member.
3. Identity Function
The type of the next function is the identity function. Example : (F:A)→(B) is the function of (A) to (B) then (F) called identity function and if the range (F) = kodomain or (F(A)=(B).
4. Square Function
The type of the function of the last mathematics is square function. The function of (F: R)→(R) which is determined by the formula (F)(X) = (AX2) (BX) (C) with (A,B,C) ∈ (R) and (A) ≠ (0) called square function.
Examples of questions and answers in the function of Mathematics :
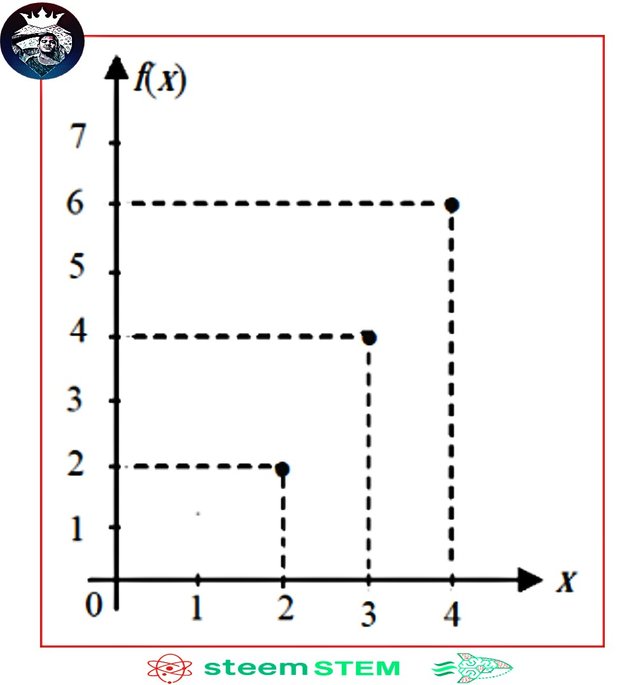
1. Known (F(X) = (AX) (B). With (F(-4 ) = -3 and (F(2) = (9) Specify the value (A) and (B) then write the function.
f(x) = ax + b
f(-4 ) = a(-4) + b = -3
-4a + b = -3 ……. (1)
f( 2 ) = a . 2 + b = 9
2a + b = 9 ……. (2)
Elimination 1 and 2 obtained :
- -4a + b = -3
2a + b = 9 –
-6a = – 12
a = 2,
Value substitution (A) = 2 to 2a + b = 9
2.(2) + b = 9
4 + b = 9
b = 5
So function (f(x) = 2x + 5
2. Which of the the set (A, B) and (C) The following is a function ?
A = {(1, 1), (2, 3), (3, 5), (4, 7), (5, 8)}
B ={(1, 6), (1, 7), (2, 8), (3, 9), (4, 10)}
C ={(2, 5), (3, 6), (4, 7)}
Answer :
That is the mapping or function is the set (A) and (C. B) not function, for on the set (B) domain (1) appears two times (relate with the value (6) and (7) to kodomain).
3. Known, if :
- A = {2, 3, 6}
B = {2, 4, 6, 8, 10, 11}
Write the domain, kodomain, range from the above relations?
Answer :
- Domain = {2, 4, 6}
Kodomain = {2, 4, 6, 8, 10, 11}
Range = { 2, 4, 6, 8, 10}
4. Note the pictures that are at the bottom of this! From the diagram of the arrow on the diagram, which diagram is a diagram of the arrow function? And give the reason.
Source Image : Google
To answer, first must understand the conditions of a relationship that can be said a function.
(I). Allegedly a function if every member (A) have one candidate against members (B)
(ii). Allegedly is not a function if there is one of the members of the (A) does not have a candidate against members (B)
(iii). Allegedly is not a function if there is a member of the (A) does not have a candidate members (B) and there is one of the members of the (A) which covers the couple members (B) more than one
(iv). And said is not a function if it is one of the members of the (A) has more than one candidate members (B)
From the examples of questions on whether you have been able to differentiate which relationships and which function? Okay until here. Hopefully can be useful for the buddy all. :)

That's post I this time, hopefully useful. And #steemSTEM has cool people who like, create, and support nerd stuff like Science, Technology, Engineering, and Mathematics related content and activities on the STEEM blockchain. If you want to be a part of it you can contribute relevant STEM content with the #steemstem tag, support and vote on steemSTEM authors, join the curation trail, hop in the Discord Channel
