Revolutionary Patterns Of Infinite Change : Can Cover The Whole World Without Repeating

In 1974, the British mathematician Roger Penrose created a revolutionary set of tiled patterns that could be laid out on infinite planes in a never-ending way. In 1982, Israel Crystallographer Daniel Shechtman found that the atomic arrangement of a metal alloy is different from the other results previously measured. Penrose won rare public recognition in the math circle, and Shechtman won the Nobel Prize. Both of these scholars defy human intuition, changed our basic understanding of the natural structure and revealed the possibility of endless changes from a highly orderly environment.

Penrose tiles, the pattern of this mathematician's hand, also have unexpected uses in materials science.
Image

The central idea of ​​the two breakthroughs is "forbidden symmetry," which is called because it is completely contrary to one's original understanding of the relationship between repetition and symmetry. The basis of symmetry is the axis of symmetry, the image appearing on one side of the axis and being completely duplicated on the other side of the axis. This relationship can be reflected in the tiled pattern in mathematics. Symmetrical graphics, such as rectangles and equilateral triangles, cover the plane without gaps or overlaps. The patterns they lay are periodic and have translational symmetry. That is, if you stagger the graphic to another location, it does not move the same way.

Penrose is a bold and passionate scholar who is less interested in single graphics and repetitions, but is boundlessly influenced by endless changes. To be exact, what he is interested in is a type of "aperiodic" tiling that consists of a number of pieces that can be seamlessly laid out on an infinity plane without repeating the pattern. This can be a dilemma because he can not use graphics with two, three, four and six axes of symmetry (such as rectangles, equilateral triangles, squares, and regular hexagons) that will be layered in a periodic pattern on an infinity plane . This means that Penrose can only rely on those that will leave gaps in the plane, that is, those that have disabling symmetry.

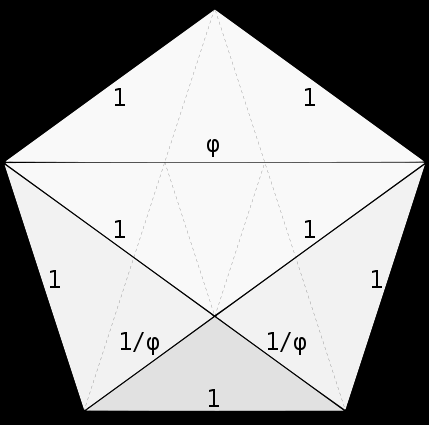
Penrose turned his mind to a regular pentagon with five axes of symmetry, trying to build his own non-repeating pattern. He once mentioned that one of the reasons is that the pentagon "looks pleasing to the eye." Penrose tiles are unique in that they do not leave unpleasant gaps due to the regular pentagonal lines and angles. They are arranged seamlessly, tossing in the plane, it is necessary to repeat, but always the answer.

Penrose Tiles to attract the public for two main reasons. One is that he found a way to create an infinitely changing pattern using just two types of tiles. The second is even more remarkable. The two types of tiles he finds are simple, symmetrical shapes that do not themselves reveal anything unusual.

Penrose designed several different versions of his aperiodic tile. The most famous set called "kite" and "darts." Kite looks just like kites played by kids, while its darts look like a simplified stealth bomber. Both are neatly split in half by the axis of symmetry, and their surfaces are also painted with two simple, symmetrical arcs. Penrose has laid down a tiling rule: "legal" collages must be able to dock arcs into continuous curves. Without this rule, the kite and dartboard will have a repeating pattern, and under this rule, there will never be any repetition. Kites and darts, danced eternally around the five symmetrical axes, combining gypsophila, ten-sided, meandering long lines with the shape of butterflies and flowers. Morphology like "like" instead, contains endless changes.

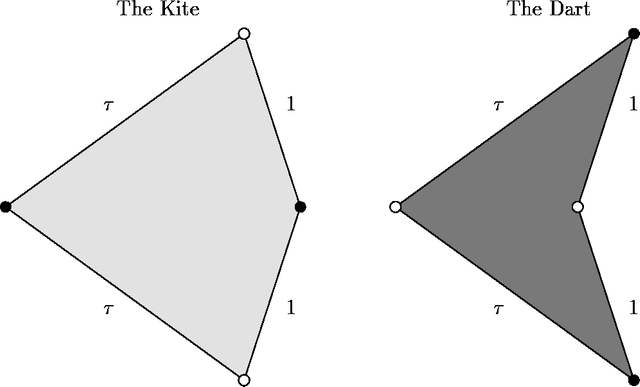
Kite and Darts: The British mathematician Roger Penrose constructs a pattern full of beauty and infinite variety with only two shapes of kites and darts (the figure in the blue line).
Image

Edmund Harriss, an assistant professor of mathematics at the University of Arkansas, holds a doctoral dissertation on Penrose tiles. He made a contrast to us: "Imagine you walk in a world of squares, and every time you walk to the edge of a square, the next one is still the same square. Keep going and you know what you see "And Penrose's tiling is exactly the opposite. "No matter how much information you have and how many tiles you've seen, you can not predict the next pattern, and it will be a pattern you've never seen before."

The non-periodic pattern on the plane has a peculiar property that the information of the arrangement location seems to be able to be passed over a large distance in some way. A tile somewhere prevents some sort of arrangement from appearing outside of hundreds (even thousands, millions) of tiles. Harris said: "Local restraints grow wildly to global constraints, and there are no periodic segments at any scale." For example, you might choose to place a kite at one place or at another Put a dart. These two things can be done, but can not be achieved at the same time.

Fibonacci proportions can be seen in these tiles, which are grouped into endless non-repeating patterns. Fibonacci ratio, also known as the "golden ratio." If, in two numbers, the ratio of the smaller to the larger number is equal to the ratio of the larger to the sum of the two, then the two numbers match the golden ratio. For tiles, the area ratio of the kite to the dart is equal to the golden ratio; the ratio of the long and short sides of the kite equals the golden ratio.

Penrose tiles can also be split into smaller tiles. The kite can be divided into two small kites and two and a half small darts; the dart can be divided into a small kite and a two-and-a-half dart. (In any reasonable collage mode, half a dozen darts can be combined in any combination.) Mathematically we treat a two-and-a-half dart as a whole.) Harris said: "Suppose I had a Penrose tiling, With A kite and B darts, after a split, I get a K + 2A + B and an A + B dart. "

Another pattern of Penrose tiles.
Image

If you split an infinite number of times, they can be thought of as spreading on an endless plane, which gives you an overall ratio of the two tiles. For this calculation, the proportion of repeating patterns must be rational numbers, if not, it means the patterns will never be completely repeated. The percentage of Penrose tiles is not only irrational but also Fibonacci Number of darts: number of kites = number of kites: total number of tiles.

Whether it is pineapple thread or rabbit breeding, Fibonacci ratio can be seen in nature. However, it is strange that a tiling system that has nothing to do with the physical world is actually based on the Fibonacci scale. Penrose's creation has been impressive in mathematics, and their unnatural combination is also very compelling. It's like he wrote a novel about a new species, and as a result zoologists really discovered the species. Penrose tiling actually linked the golden ratio of this manually invented mathematical concept to the mathematics around us.

Image

When Penrose accepted the disabling symmetry, he did not yet know that he was already in the midst of a new trend of revolution in material science. After all, symmetry has been the foundation of pure mathematics and the natural world. Astronomer Mario Livio calls symmetry "one of the most fundamental tools in breaking nature's design." The reason why nature uses squares and regular hexagons is the same as that of human designers: they are simple, orderly, and efficient. If pentagons are impractical in the simple interior design of tiling patterns, they are unlikely to appear in solid materials like crystals.

After all, crystals are three-dimensional grids of atoms that grow by adding atoms and expanding rasters, a process that works best when atoms are combined in a repetitive manner. For decades, the notion of crystal stopped here: the crystal is a repeating structure, nothing more.

Then in 1982, Sheikh Tuttle left the Israel Haifa Polytechnic for an academic leave and came to the National Bureau of Standards. He labored in the laboratory there with aluminum-manganese alloys, but the diffraction pattern of the alloy did not show any standard symmetry known to the crystallographer. In fact, their atomic arrangement seems to resemble those of regular pentagons, rhombuses, kites and darts that Penrose whipped whirlwinds in the mathematical world.

Shechtman said: "Of course I'm familiar with Penrose tiling." But he could not think of them as alloys. "I do not know what the image reflects, and I repeat the experiment over and over again in the coming months until the vacation is almost over, and I fully understand that it is not what it is, but I still do not know what it is."

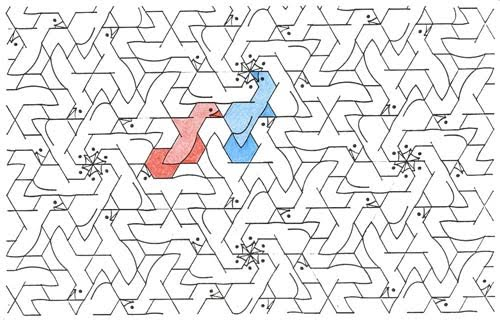
To understand what he had discovered, Shechtman, like Penrose, challenged the same intuition and common sense. He had to accept the perplexed and non-repetitive nature of disabling symmetry and pentagons. After returning to Israel, Shechtman reluctantly concluded that he found a non-repetitive structure of crystalline atoms. But like the rest of the material science, he was unwilling, at first, to call his discovery "crystals," quasicrystal.

It is as if Penrose's fantastic math has been killed in nature. Sheikh Thamman said: "Crystals have been defined as 'ordered and cyclical' for 80 years because the crystals studied have been periodic since 1912. Until 1992, the International Union of Crystals The formation of a committee redefined the 'crystal', a paradigm shift in crystallography. "

Understand that the difficulty of absorbing Sheikh Thamman's discovery lies not only in breaking the inertia of thinking. Aperiodic crystal structure is not only unfamiliar, but also considered unnatural things. Recall that the location of a Penrose tile can affect the placement of thousands of tiles outside the tile, resulting in global constraints. If the crystal is a pile of atoms, then there should be no laws of nature that would allow Penrose's inner constraint to exist.

As a result, people found that crystals are not always stacked together by atoms. Sheikhtmann said: "Intermetallics are extremely complex and have a large unit cell size. They are not local." If the crystals do not accumulate but form large pieces at a time, atoms that are far apart Like Penrose tiling, affect each other's position.

Disabling symmetry, like many taboos, has finally been accepted as a logical form of natural existence. Quasicrystals have not only become the subject of new academic fields, but also their unusual structure has many useful properties. For example, irregular atomic configuration can reduce the surface energy of the material, making it difficult to stick with other substances. Quasicrystals can therefore be used as a non-stick surface material. (When Penrose invented his new tile, there was no expectation that it would blossom in the field of crystallography, let alone fried eggs.) Quasicrystals also tend to have lower coefficients of friction and less wear and tear Therefore, razors and surgical appliances such sharp contact with the body tools, quasi-crystal can be ideal for coating.

Holmium - manganese - zinc quasicrystal electron diffraction.
Image

Since quasi-crystal structure never repeated, they will form a unique diffraction pattern under the electromagnetic wave. Photoelectron researchers are interested in how they affect the light transmission, refraction, and photoluminescence effects. Quasi-crystal in the cold state, the resistance will soar near infinity. They can absorb infrared radiation, heat quickly. This makes them a high value additive for 3D printing. 3D printing usually uses plastic powder as the main raw material. When it is mixed with quasicrystalline powder, the quasi-crystal powder rapidly heats up when it is irradiated with infrared light and melts the surrounding plastic particles to make them stick together.

No one knows how the story of disabling symmetry ends. Mathematicians continue to explore the nature of Penrose tiles, quasi-crystal is still the subject of basic and applied research. But they have gone through an incredible journey. In the past 40 years, the five-axis symmetry has become impractical by becoming unrealistically valuable, transforming nature from being contrary to nature into a mainstream subject from deviatio. We would like to thank those two scholars for this shift in their efforts to promote the further development of traditional concepts, thereby revealing new forms of infinite change in nature.

---

References for Text and Images:

• https://en.wikipedia.org/wiki/Penrose_tiling
• http://graceavery.com/settlers-of-catan-penrose-tiles/
• http://intendo.net/penrose/images_9.html
• http://mathworld.wolfram.com/PenroseTiles.html
• https://plus.maths.org/content/roger-penrose-knight-tiles

---

Support @steemstem and the #steemstem
project - curating and supporting quality STEM
related content on Steemit