Saludos queridos lectores, bienvenidos nuevamente a mi Blog. En está oportunidad les hablare un poco acerca de Interpolación Polinomial usando el entorno GNU Octave | 1^era Parte, en especifico aquí mostraremos como usar dicho entorno para realizar interpolación polinomial, en especifico la aproximación de Vandermonde, y de Newton, propiedades y ejemplos. La misma está dirigida al público en general (aunque debemos acotar, este es un tema de un nivel más alto, para el que es necesario tener de algunos conocimientos previos de análisis real, cálculo avanzado, entre otros más), con atención especial a profesionales y estudiantes universitarios en ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

---

---

El entorno GNU Octave

El entorno GNU Octave es un lenguaje de scripting científico muy similar al entorno MATLAB. Sin embargo, es importante resaltar que el nacimiento de GNU Octave no esta ligado al entorno MATLAB, sin dejar de mencionar que poco a poco ha ido convergiendo hacia la compatibilidad.

El inicio de Octave, estaba inicialmente destinado para ser usado como un software complementario para un libro de nivel universitario sobre diseño de reactores químicos, escrito por James B. Rawlings de la Universidad de Wisconsin-Madison y John G. Ekerdt de la Universidad de Texas.

Actualmente, Octave es mucho más que solo otro paquete para un curso, con una utilidad ilimitada más allá de un salón de clases. Aunque los objetivos iniciales eran algo vagos, sus autores querían crear algo que permitiera resolver problemas más reales. Octave es un software bajo los términos de la Licencia Pública General de GNU.

---

---

Aproximación Polinomial

En el problema de la aproximación de datos, se dan algunos puntos, digamos (x₁, y₁), (x₂, y₂), . . . , (x_n, y_n) y se pide encontrar una función g(x) que capture la disposición de los datos. Si la disposición es de decaimiento (o decrecimiento), entonces podemos buscar una función g(x) de la forma

Si en cambio la tendencia de los datos es oscilatoria, una aproximación trigonométrica podría ser la más apropiada. Existen otros ajustes, lo cuales podría requerir una aproximación con un polinomio de orden bajo. Pero lo que es de notar, es que independiente del tipo de función utilizada, hay muchas formas o medidas para llegar o obtener el éxito.

Un caso espacial del problema de aproximación de datos, es cuando se requiere que la función g(x) pase exactamente por cada uno de los datos, como podemos apreciar en la Figura siguiente.

_{Imagen construida con GNU Octave, por @abdulmath.}
Esto significa que g(x_i) = y_i, para todo valor de i=1:n y entonces decimos que g interpola los datos.

El problema de interpolación polinomial es particularmente importante:

Así, el polinomio p₂(x) = 1 + 4x-2x² interpola los puntos (-2, -15), (3, -5) y (1, 3). Tal como lo podemos apreciar en la figura anexa.

_{Imagen construida con GNU Octave, por @abdulmath.}
Para cada par ordenado (x_i, y_i) se puede considerar como una instantánea de alguna función f(x) tal que y_i = f(x_i).

La función f puede estar disponible explícitamente, como cuando queremos interpolar a la función sen(x) en x = 0, x = π/2 y x = π con una cuadrática. También f se puede definir implícitamente, como en el caso cuando queremos interpolar la solución de una ecuación diferencial en un número discreto de puntos o nodos. Es por ello que la interpolación polinómica gira alrededor de como expresar su representación, como calcularse, y como evaluarse.

1. ¿Cómo representamos el interpolador p_n-1(x)? En lugar de elegir expresar los términos interpolantes de la base usual de polinomios 1, x y x², podríamos usar una base alternativa, por ejemplo, 1, (x + 2) y (x + 2)(x - 3). Así
   
   
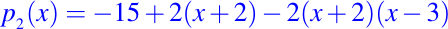
   es otra forma de expresar el interpolador cuadrático de los datos (-2, -15), (3, -5) y (1,3). Por lo tanto, diferentes bases tienen diferentes virtudes computacionales.
2. Una vez que nos hemos fijado una representación para el polinomio interpolante, ¿cómo determinamos los coeficientes asociados? Resulta que este aspecto del problema implica la solución de un sistema lineal de ecuaciones con una matriz de coeficientes altamente estructurados.
3. Después de haber calculado los coeficientes, ¿cómo se puede evaluar el interpolador con eficiencia? El acto de trazar un interpolador polinómico arroja luz sobre el problema de evaluación y es un buen escenario para discutir la tensión entre la vectorización y la complejidad aritmética. Además, la visualización del polinomio interpolante motiva algunas de sus propiedades matemáticas.

---

---

La Aproximación de Vandermonde

En la aproximación de Vandermonde, el interpolador se expresa como una combinación lineal de 1, x, x², x³, etc. Aunque los monomios no son la mejor opción para una base, nuestra familiaridad con esta forma de "trabajar negocios" con polinomios los convierte en una buena opción para iniciar nuestra discusión.

---

Un problema de interpolación de cuatro puntos

Encontremos un polinomio cúbico

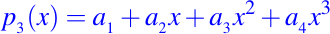
que interpole los puntos o datos siguientes: (-2,10), (-1,4), (1,6) y (2,3). Cada punto o dato a interpolar induce a una ecuación lineal que relaciona las cuatro incógnitas a₁, a₂, a₃ y a₄, las cuales mostramos a continuación:


Expresando estas cuatro ecuaciones en términos matriciales/vectoriales tenemos


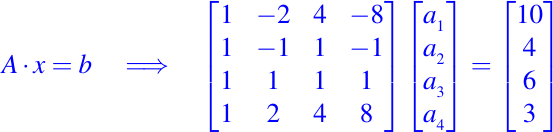
La solución es


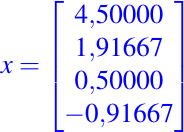
de el sistema 4x4 la podemos encontrar de la siguiente manera usando Octave:


_{Código en GNU Octave.}

---

El caso general de n puntos

A partir del ejemplo anterior, el problema de interpolación polinomial se reduce a un problema de ecuaciones lineales. En general, el objetivo es determinar a₁, a₂, . . . ,a_n, de modo que si

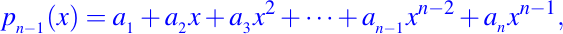
entonces


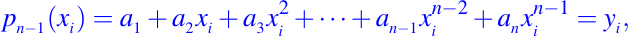
para i = 1:n. Escribimos estas ecuaciones en la forma matricial/vectorial, obtenemos


Designemos la matriz de coeficientes por V. La resolubilidad del problema de interpolación depende de la no singularidad de la matriz V. Supongamos que existe un vector c tal que Vc = 0. Deducimos que el polinomio


es cero en x = x₁, x = x₂, . . . , x = x_n. Esto nos dice, que tenemos un polinomio de grado n - 1, con n raíces. La única forma que suceda el anterior hecho, es cuando el polinomio q(x) es el polinomio cero, es decir, c = 0. Por lo tanto, V es no singular.

---

---

Configuración y resolución del sistema

Detallemos la construcción de la matriz de Vandermonde, a la cual llamamos V. El primer método se basa en la observación de la fila i de V involucra potencias de x_iy dichas potencias se van incrementando de 0 a n - 1 a medida que vamos avanzando de izquierda a derecha. Un enfoque convencional de doble bucle dado

_{Script para construcción de la Matriz Vandermonde en GNU Octave. Elaborado por @abdulmath.}
Los algoritmos que operan en una matriz bidimensional fila por fila están orientados a la fila. El bucle interno del script anterior se puede vectorizar porque Matlab admite la exponenciación punto por punto. La i-ésima fila de V requiere la potencia del escalar x_i por cada uno de los valores en el vector fila 0:n - 1 = (0, 1, . . . , n - 1). Así,
row = (x(i)*ones(1,n)).^(0:n-1)
asigna el vector (1, x_i, x_i², x_i³, . . . , x_i^n-1) a row, mas precisamente, los valores que conforma la fila i de V. La fila i de V puede ser referenciada por V(i, :), y así obtenemos


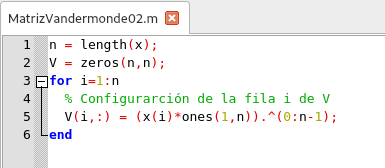
_{Script para construcción de la Matriz Vandermonde en GNU Octave. Elaborado por @abdulmath.}
Al invertir el orden de los bucles en el script de configuración original, obtenemos un algoritmo orientado a columnas:


_{Script inverso para construcción de la Matriz Vandermonde en GNU Octave. Elaborado por @abdulmath.}
Si j > 1, entonces V(i, j) es el producto de x(i) y V(i, j - 1), la entrada de la matriz a su izquierda. Esto sugiere que las potencias requeridas se pueden obtener mediante multiplicación repetida:


_{Script para construcción de la Matriz Vandermonde por columnas en GNU Octave. Elaborado por @abdulmath.}

La generación de la columna j-ésima implica la multiplicación vectorial puntual:

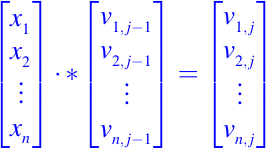
y esto puede implementarse por
V (:,j) = x.*V (:,j-i)
Basándonos en nuestra implementación final en esto, obtenemos


_{Script para la interpolación de Vandermonde en GNU Octave. Elaborado por @abdulmath.}

---

---

Multiplicación anidada

Ahora consideremos la evaluación de

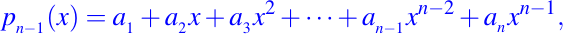
en x = z, asumimos que z y a(1:n) son conocidos. La rutina de aproximación es


_{Script para la Multiplicación anidada en GNU Octave. Elaborado por @abdulmath.}
asignado el valor de p_n-1(z) a pval. Un algoritmo mas eficiente es basado en la organización anidada de el polinomio, el cual lo ilutraremos para el caso = 4:


Notemos que el fragmento
pval = a(4);
pval = z*pval + a(3);
pval = z*pval + a(2);
pval = z*pval + a(l);
asignando el valor de p₃(z) a pval.

Para el caso general, esta idea de multiplicación anidada toma la siguiente forma:

_{Script para la Multiplicación anidada general en GNU Octave. Elaborado por @abdulmath.}
Esto es ampliamente conocido como la Regla de Horner.

Antes de crear una función en Octave de la idea de Horner, examinemos el caso en que el interpolador debe evaluarse en muchos puntos diferentes. Para ser precisos, supongamos que z(1:m) es un vector, queremos asignar el valor de p_n-1(z(i)) a pval(i). Un enfoque obvio es simplemente repetir la iteración de Horner precedente en cada punto:

Se puede obtener una versión vectorizada de este fragmento si pensamos en la evaluación simultánea de los interpolantes en cada z_i. Supongamos que m = 5 y n = 4 (es decir, el caso cuando el interpolante cúbico sera evaluado en cinco puntos diferentes). El primer paso en las cinco aplicaciones de la idea de Horner se puede resumir de la siguiente manera:

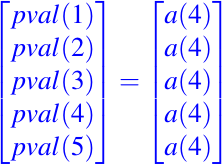
En términos de vectores
pval =a(n)*ones(m,1)
El siguiente paso requiere una multiplicación agregada de la siguiente forma:



Es decir,
pval = z.*pval + a(3)
El patrón es claro para el caso cúbico:
pval = a(4)*ones(m,1);
pval = z .*pval + a(3);
pval = z .*pval + a(2);
pval = z .*pval + a(1);
Así, podemos generalizarlo de la manera siguiente:


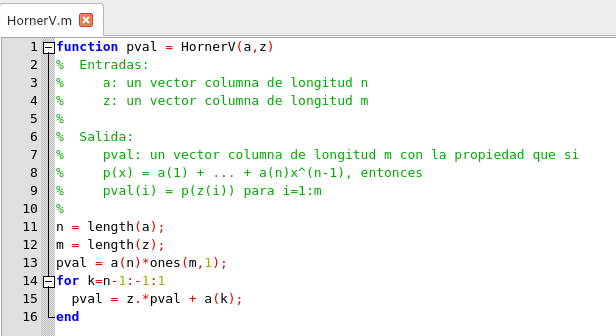
_{Script para la Regla de Horner en GNU Octave. Elaborado por @abdulmath.}

Como aplicación, a continuación presentamos un script que muestra interpolaciones cúbicas de la función sen(x)+cos(x) en [0, 2π].

_{Script para la Aplicación en GNU Octave. Elaborado por @abdulmath.}

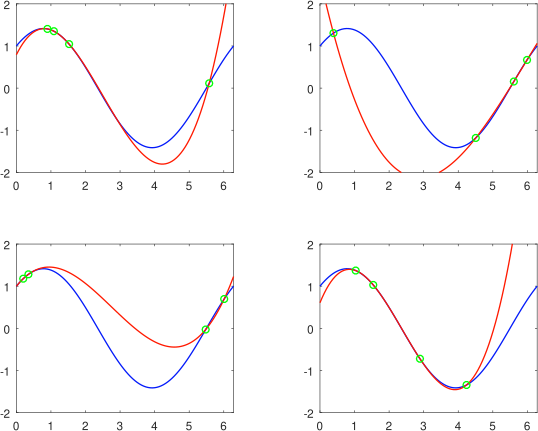
_{Gráficos de la Aplicación en GNU Octave. Elaborado por @abdulmath.}

---

---

Queridos amigos y lectores, espero hayan disfrutado y aprendido acerca de la Interpolación Polinomial usando el entorno GNU Octave | 1^era Parte, de igual manera los invito para la 2^da Parte de este tema, donde continuaremos mostrando el desarrollo del mismo con los script y aplicaciones. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

• Demidovich, B. P., and I. A. Maron. Computational Mathematics Mir, Moscow, 1976.
• Björck, Åke. Numerical methods in matrix computations. Vol. 59. Cham: Springer, 2015.
• Burden, Richard L., and J. Douglas Faires. Numerical analysis. Ninth Edition. Cengage Learning. 2011.

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, GNU Octave, , GIMP e Inkscape.

---

---

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

_{Imagen diseñada con GIMP y elaborada por @abdulmath.}