Cálculo Matricial | 2da Parte

Saludos queridos lectores, bienvenidos nuevamente a mi Blog. Continuando con el tema del Cálculo Matricial, en esta oportunidad tocaremos algunos aspectos de las operaciones matriciales, en específico trataremos de ilustrar la multiplicación de una matriz por un vector, y la multiplicación entre matrices, dejando para el final una sección acerca de la eficiencia de estas operaciones a través de diversas normas o medidas de distancias, vista desde un punto de vista geométrico, y el error al medirlas. Es bueno mencionar, que el interés al desarrollar este tema, más que mostrar la teoría envuelta en el mismo, es recalcar de que manera podemos implementar estas operaciones con el uso de un computador con un software matemático como GNU Octave, el cuál es un Software Libre, o para aquellos que posean una Licencia de un Software súper conocido y usado por muchos como lo es Matlab. Esta serie de publicaciones están enfocadas o dirigida a estudiantes, profesionales e investigadores en algunas áreas como física, química, biología, ciencias sociales, humanidades, entre otras que deseen utilizar algunas de estas estructuras matemáticas de mucha utilidad en la simplificación de problemas respectivos en sus áreas. Estoy abierto a sus comentarios y dudas que puedan surgir dentro del tema. Sin perder más tiempo, comencemos. _{Presentación Cálculo Matricial. Elaborado por @abdulmath.}

Ahora bien, como vimos en nuestra publicación anterior (Cálculo Matricial | 1era Parte), una vez que tenemos la matriz bien configurada o estrucurada, podemos realizar operaciones matriciales como productos o multiplicaciones de una matriz por un vector y mutliplicación entre matrices. Aunque estas operaciones se pueden realizar con una sola línea de comando en Octave, es instructivo explorar las diferentes maneras en que las mismas pueden ser implementadas.

---

---

Sin perdida de generalidad, podemos suponer que tenemos una matriz A de tiene m filas con n columnas, cuyas entradas o valores en cada posición son números reales, lo cual en notación matemática lo podemos escribir como sigue:

y deseamos calcular el producto o multiplicación de una matriz por un vector, es decir, necesitamos calcular y = Ax donde A es la matriz configurada inicialmente y x es el vector por el cual queremos hacer la multiplicación, cabe resaltar que dicho vector debe contener la misma cantidad de entradas en forma de columna, como la cantidad de columnas de la matriz dada. En otras palabras el vector tiene n filas, y una sola columna, por lo que comúnmente se conoce como vector columna.

La manera usual de proceder con este cálculo es calcular los productos de puntos, es decir cada valor del nuevo vector sera el producto que mostraremos a continuación para cada valor de i=1: n

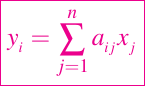
Ahora bien, dicha operación de suma de productos, la podemos resumir en el siguiente script o algoritmo que mostraremos a continuación:


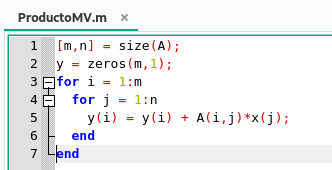
_{Algoritmo para calcular el producto de una matriz por un vector en GNU Octave. Elaborado por @abdulmath.}
Ahora bien, hacer la operación anterior o escribir la siguiente línea de comando y = A*x son equivalentes y requiere 2mn flops o operaciones de punto flotante.

Aunque en Octave no es necesario realizar la multiplicación de una matriz por un vector de forma manual, es instructivo reconsiderar el doble bucle anterior. En particular, reconociendo que el bucle sobre j del producto interno entre la fila i-ésima de A por el vector x, entonces podemos escribir la siguiente función para esta operación:

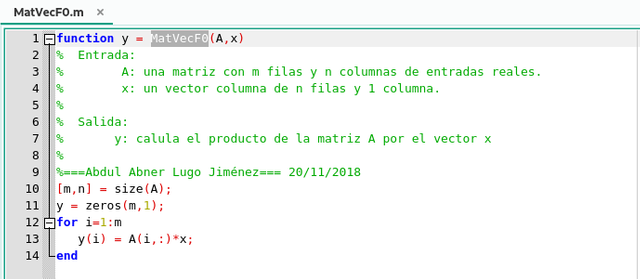
_{Algoritmo para optimizar el calculo del producto de una matriz por un vector usando las filas de la matriz A en GNU Octave. Elaborado por @abdulmath.}
El procedimiento está orientado a las filas porque se tiene acceso a la matriz A a través de las filas.

Ahora un algoritmo orientado a las columnas también se puede desarrollar. Para ello, iniciemos con una observación de una matriz de 3 filas por 2 columnas:

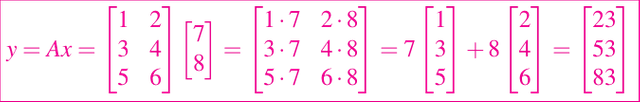
En otras palabras, el valor de y es una combinación lineal de las columnas de A con multiplicadas por los elementeos del vector x, siendo estos los coeficientes de la combinación lineal. Esto nos lleva a tener el siguiente algoritmo para la multiplicación de una matriz por un vector a través de las columnas de A:


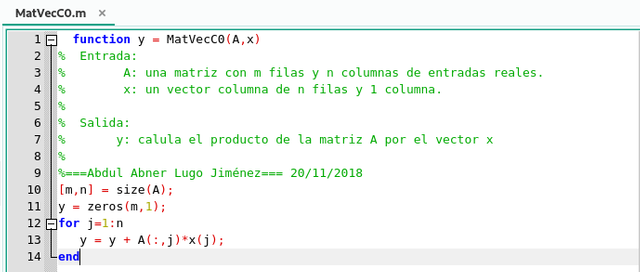
_{Algoritmo para optimizar el calculo del producto de una matriz por un vector usando las columnas de la matriz A en GNU Octave. Elaborado por @abdulmath.}
En términos de programación, esta función es solo intercambiar los bucles o ciclos de i y j en la función MatVecF0


Esto se conoce como la operación saxpy, la cual junto al producto punto, es un actor clave en los cálculos matriciales. A continuación podemos mostrar una vista más formal de la operación saxpy en la función MatVecC0: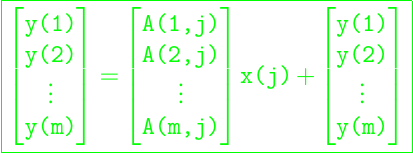

La función MatVecC0 requiere 2mn flops al igual que la función MatVecF0. Sin embargo, tenemos que resaltar una vez más las limitaciones del conteo de la flops, ya que en diferentes entornos informáticos potentes los dos algoritmos que hemos desarrollaods para la multiplicación de una matriz por un vector podrían ejecutarse a velocidades radicalmente diferentes.

Por ejemplo, si las entradas de la matriz a_ij se almacenan columna por columna en la memoria, entonces la versión saxpy accede a las entradas de A que son contiguas en la memoria. Por el contrario, el algoritmo orientado a filas accede a a_ij de forma no contiguo. Como resultado de ese inconveniente, puede requerir mucho más tiempo para ejecutarse.

---

---

En muchos casos las matrices están estructuradas con muchos ceros. Es por ellos que es necesario poder racionalizar los cálculos. Podemos entonces pensar en el siguiente ejemplo para ir visualizando lo que queremos decir, sea una matriz triangular superior con 4 filas y 4 columnas y el vector un vector de 4 filas y una columna, es decir, tenemos el siguiente problema que ilustramos a continuación

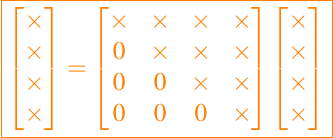
La derivación del proceso, comienza con examinar la función MatVecF0. Observemos los productos internos en el bucle o ciclo


implican largas series de ceros cuando A es triangular superior. Ahora si en vez de ser una matriz de 4 filas y 4 columnas, tenemos una matriz de 8 filas y 8 columnas y un vector de 1 fila y 8 columnas, la cual podemos visualizar a continuación


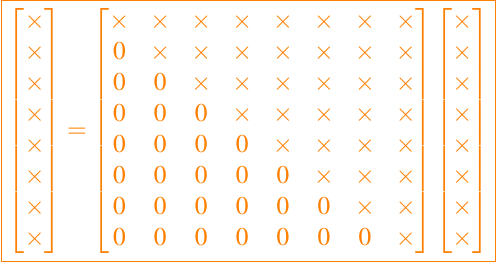
entonces si nos enfocamos en el producto de la fila 6, por el vector, es decir, A(6, :)*x el mismo tiene el siguiente aspecto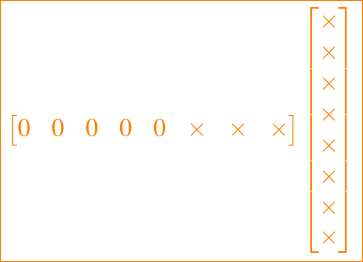


y requiere un número reducido de flops debido a todos los ceros. Por lo tanto, debemos sortear los productos interiores para que sólo incluyan la parte que no sea cero de la fila.

Como observamos las primeras entradas de A(i,:) son cero, vemos que A(i,i:n)*x (i:n) es la parte distinta de cero del producto interno completo A(i,:)*x que necesitamos. De ello se deduce el siguiente bucle o ciclo

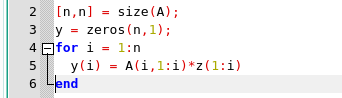
es una versión para matrices triangulares superiores de MatVecF0 que aprovecha la estructura. La asignación a y(i) requiere 2i flops o operaciones de punto flotante por segundos, por lo tanto de manera general tenemos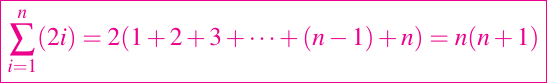


las operaciones de punto flotante por segundo o flops son obligatorios. Sin embargo, de acuerdo con la filosofía del conteo de flops, no nos importa el término O(n), por lo que nos limitamos a afirmar que el algoritmo requiere n² flops. Nuestra racionalización redujo a la mitad el número de operaciones punto flotante.

La función MatVecC0 también la podemos optimar en este sentido. Teniendo en cuenta que A(:,j) es cero en las componentes j + 1 hasta n, por lo tanto saxpy es esencial en en el paso j es:

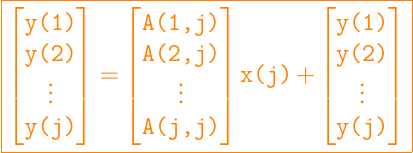
la representación del algoritmo quedaría como sigue


Una vez más, el número de operaciones punto flotante por segundo se ve reducido a la mitad.

---

---

Para poder realizar la operación de multiplicación de matrices, es necesario que se cumplan una condición muy importante, que si queremos multiplicar 2 matrices, digamos A y B donde la matriz A tiene m filas y r columnas, por lo tanto la matriz B debe tener la misma cantidad de filas que la cantidad de columnas que A, es decir, debe tener r filas y n columnas. Por lo tanto podríamos formalizar matemáticamente de la siguiente manera: Supongamos que tenemos dos matrices,

entonces el producto C = AB lo podemos definir cada entrada de la matriz C, de la siguiente manera


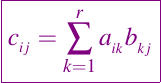
para todos los valores de i entre 1 y m, los valores de j entre 1 y n. En otras palabras, cada entrada de la matriz C es el producto interno entre una fila de A y una columna de B. De este modo, el algoritmo siguiente


_{Algoritmo para calcular el producto de dos matrices en GNU Octave. Elaborado por @abdulmath.}
calcula el producto AB y asigna el resultado a C. En Octave la multiplicación de matrices es soportada de manera nativa, por lo que esto puede implementarse con la línea única de código C = A*B.

Sin embargo, hay un número de maneras diferentes de ver la multiplicación de matrices, y acá presentaremos cuatro versiones distintas de esta multiplicación. Ahora bien, comencemos con la primera, haciendo un reconocimiento de que el bucle más interno del algoritmo anterior vigila el producto punteado entre la fila i de A y la columna j de B, el cual podemos ver en la siguiente función que construimos

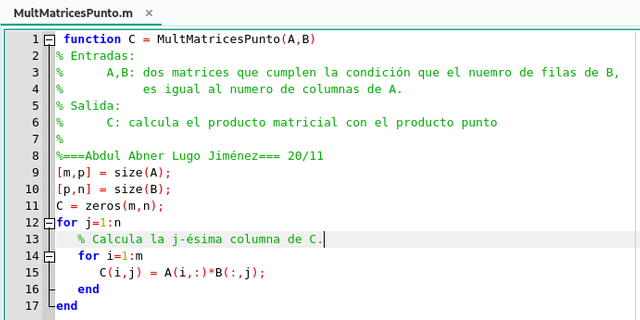
_{Función del algoritmo para la multiplicación de matrices usando el producto punto en GNU Octave. Elaborado por @abdulmath.}

Por otro lado, sabemos que la columna j de C es igual a la matriz A por la columna j de B. Si aplicamos la función MatVecC0 a cada uno de estos productos de matriz por un vector, obtenemos el segundo algoritmo para multiplicación de matrices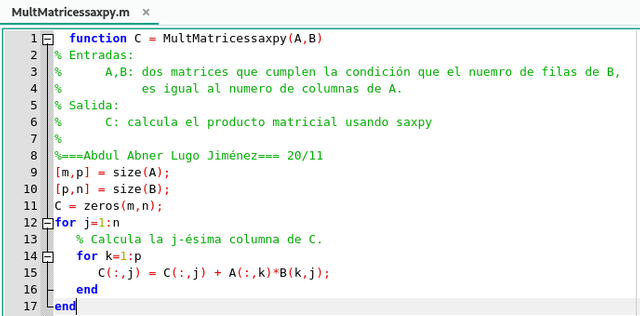


_{Función del algoritmo para la multiplicación de matrices usando saxpy en GNU Octave. Elaborado por @abdulmath.}
Esta versión de la multiplicación de matrices destaca la operación saxpy. Reemplazando el bucle interno por una multiplicación de una matriz por un vector único se obtiene el tercer algoritmo para la multiplicación de matrices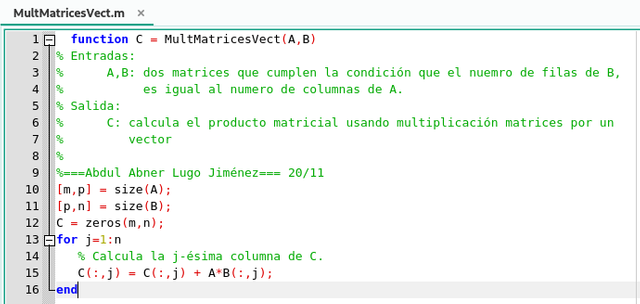


_{Función del algoritmo para la multiplicación de matrices usando la multiplicación de matrices por vectores en GNU Octave. Elaborado por @abdulmath.}
Finalmente, observamos que una multiplicación de matriz es una suma de productos externos. El producto exterior entre un vector columna u de m componentes y un vector fila v de n componentes viene dado por la siguiente ecuación:


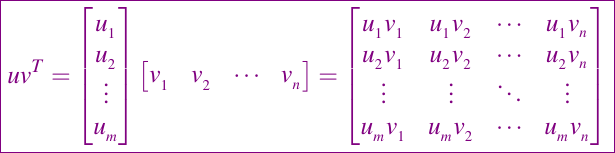
Podemos pensar esta multiplicación como una multiplicación ordinaria de dos matrices, una de m columnas por 1 fila y la otra como una matriz de 1 fila por n columnas. Por ejemplo


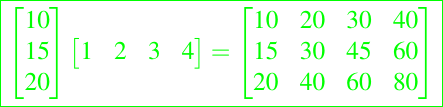
Volviendo al problema de la multiplicación de matrices, tenemos


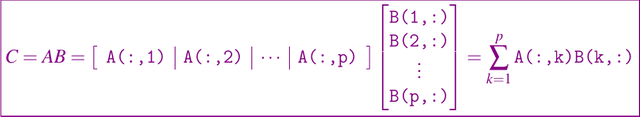
Así, tenemos por ejemplo lo siguiente:


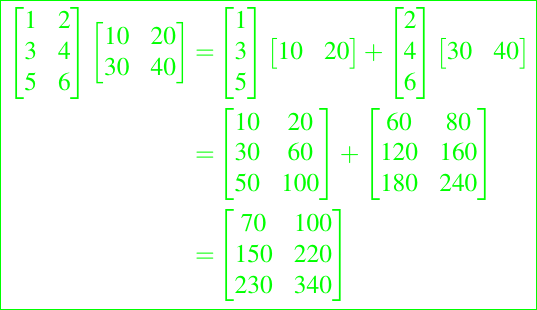
Esto lleva a la versión de producto externo de la multiplicación de matrices, el cual podemos ilustrar en e siguiente algoritmo que sería la cuarta versión para realizar los productos o multiplicación de matrices.


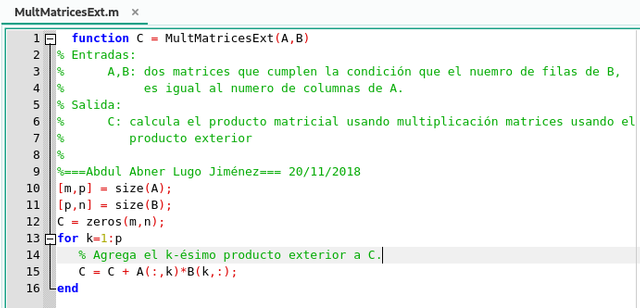
_{Función del algoritmo para la multiplicación de matrices usando el producto exterior en GNU Octave. Elaborado por @abdulmath.}
Entonces podemos compara las cuatro funciones de multiplicación de matrices que hasta ahora hemos desarrollado junto con el comando directo C=A*B. Esta comparación la hacemos con el siguiente srcitp de comandos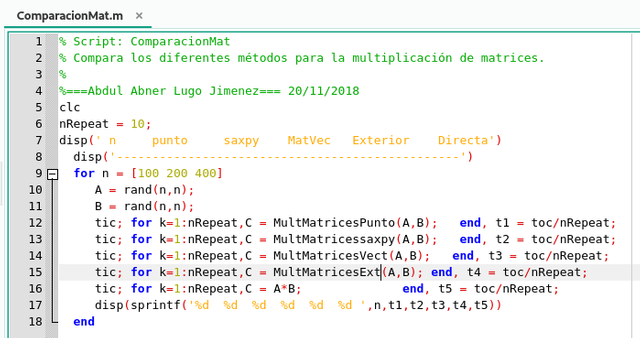


_{Script de comparación ComparacionMat para la multiplicación de matrices en GNU Octave. Elaborado por @abdulmath.}
El tabla que se muestra a continuación no se reportan los valores reales del cálculo, lo que muestra es la debilidad del conteo de las operaciones punto flotante por segundo. Los métodos para el mismo problema que involucran el mismo número de flops pueden funcionar de manera muy diferente. La naturaleza de la operación del núcleo (saxpy, producto punto, producto matriz por un vector, producto externo, etc.) es más importante que la cantidad de aritmética implicada.

n	Punto	saxpy	Matriz por Vector	Exterior	Directo
10	0.400	0.617	0.067	0.100	0.017
20	1.583	2.333	0.150	0.500	0.050
40	6.567	10.067	0.550	3.333	0.367
80	29.083	49.733	3.033	25.517	2.617

---

---

Para concluir esta publicación daremos una breve pero importante atención a la manera de cuantificar los errores en el área de cálculo matricial. Para ello, necesitamos el concepto de norma. Las normas son un vehículo para medir la distancia en un espacio vectorial. Sea un vector x en el espacio vectorial más común, Rⁿ, entonces las siguientes normas son de una particular importancia, a saber:

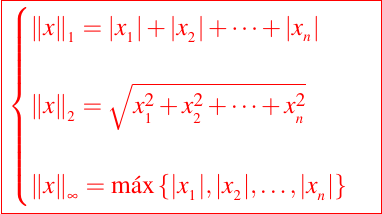
Una norma es solo una generalización del valor absoluto. Siempre que pensamos en los vectores de errores en un sentido de orden de magnitud, entonces la elección de la norma generalmente no es importante. Es posible mostrar que


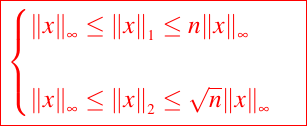
En Octave, si x es un vector, la instrucción norm(x,1), norm(x,2) y norm(x,inf) pueden ser utilizadas para determinar estas cantidades.

La idea de una norma se extiende a las matrices, como en el caso de los vectores, hay varios casos especiales importantes. Si A es una matriz con m filas y n columnas, entonces tenemos:

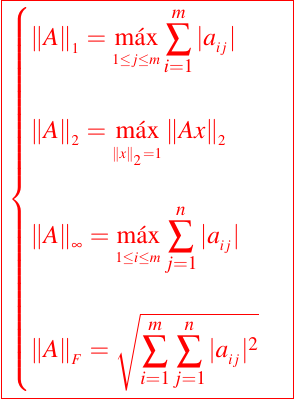
En Octave si A es una matriz, entonces se pueden usar las siguientes intrucciones norm(A,1), norm(A,2), norm(A,inf), y norm(A,'fro') para calcular estos valores. Como una simple ilustración de cómo las normas de la matriz pueden ser usadas para cuantificar el error a nivel de la matriz, mostraremos el siguiente resultado sobre los errores de redondeo que surgen cuando se almacenan matrices de m filas y n columnas.

Si C es la matriz almacenada de una matriz A con m filas y n columnas, entonces C = A + E, donde E es una matriz del mismo orden que A, y se satisface la siguiente relación

Esto nos dice que los errores de orden eps|| A ||₁ se producen cuando se almacena una matriz A real en punto flotante. Resultados similares se pueden obtener si usamos las otras normas definidas anteriormente.

---

---

Queridos amigos y lectores, espero hayan disfrutado de esta segunda entrega de este tan apasionante e interesante tema del cálculo numérico, Cálculo Matricial | 2da Parte apoyado con el entorno GNU Octave, en esta oportunidad pudimos estudiar dos operaciones matriciales muy importantes, así como usarlas de diferentes enfoques y como optimizar su aplicación de acuerdo a las estructuras de las matrices. Espero que el mismo sea de apoyo a ustedes en sus trabajos, o investigaciones y aplicaciones a sus áreas de estudio, gracias por tomar un poco de su tiempo y poder disfrutar un poco más del maravilloso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

• Hoffman, K., and Kunze, R. Álgebra lineal. Prentice-Hall Hispanoamericana. 1973.
• Demidovich, B. P., and I. A. Maron. Computational Mathematics Mir, Moscow, 1976.
• Björck, Åke. Numerical methods in matrix computations. Vol. 59. Cham: Springer, 2015.
• Burden, Richard L., and J. Douglas Faires. Numerical analysis. Ninth Edition. Cengage Learning. 2011.

---

La imagen de fondo de la portada es una imagen de libre uso tomada de

---

---

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.