¡Saludos para todos! Bienvenidos a mi Blog. Quisiera compartir en esta oportunidad con todos ustedes queridos lectores, de una aproximación de la función seno, del matemático indio Bhaskara o Bhaskara I. En esta oportunidad les presento una comparación de la aproximación antes mencionada, con otras aproximaciones conocidas de la función seno, el estudio lo haremos midiendo el error con la norma del máximo, la norma L², el calculo del error relativo. Esta publicación esta dirigida al público en general, y todos los curiosos y amantes de las ciencias exactas y numéricas. Espero que les guste, y puedan apreciar este aporte. Sin perder más tiempo, iniciemos.

---

---

¿Quien es Bhaskara I?

La información que se tiene de Bhaskara o también conocido como Bhaskara I, es muy escueta o casí toda deducida de sus escritos. Posiblemente su nacimiento es muy cercano a los año 600 y muy posiblemente en la ciudad de Saurastra, India, actualmente el estado de Gujarat, y la fecha de su muerte es muy cercana a los años 680 la cual posiblemente fue en la ciudad de Asmaka, en la India.

Bhaskara I fué un eminente matemático de la India, como un educación en astronomía debido a la educación impartida por su Padre, además es considerado uno de los estudiantes con mayor relevancia e impacta de la escuela de astronómica de Aryabhata. Otra de los aportes de Bhaskara I, fue que se conoce como supuestamente el primero escribir los números en el sistema decimal indio-arábigo; en esta representación denoto el número cero con un círculo.

Adicionalmente en el año 629, muestra una extraordinaria, impresionante y única aproximación racional de la función seno, que fue publicada en sus comentarios sobre el trabajo de Ariabhatíia, el cual se conoce por estar escrito en versos, este trabajo era sobre astronomía matemática. En dichos comentarios considero ecuaciones variables y fórmulas trigonométricas.

---

---

Motivación

Quisiera hablarles un poco de lo que me llevo a realizar esta publicación. Hace unos meses atrás, mientras leía una de mis redes sociales (Twitter), me consigo con un Tweet de una de las cuentas que sigo, Fermat's Library, colocaron el Tweet de la imagen que esta al inicio de la publicación, donde comentan que hace 1400 años se dio una aproximación de la función seno, pero lo extraño y que me causo curiosidad fue que dicha aproximación era racional y que solo estaba dada entre 0 y pi. Pero no solo eso, sino que la misma data aproximadamente en el Siglo VII, la cual fue presentada por un matemático indio que hasta el día de hoy desconocía de su existencia.

La información que se consigue de este matemático indio es muy poca, la misma la podemos encontrar en [1] y [2]

---

---

Aproximación de la función Seno

A continuación mostraremos las aproximaciones de la función seno que estaremos usando para la comparación y calculo del error. Usaremos la aproximación de Bhaskara I y la aproximación por Series de Taylor de diferentes ordenes.

Aproximación de Bhaskara I

La aproximación de Bhaskara I fue presentada en el trabajo Maja-bhaskaríia el cual esta estructurado por ocho capítulos que tratan acerca de la astronomía matemática. En el, presenta la notable fórmula de aproximación para la función seno, que es

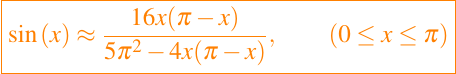
Aproximación por Serie de Taylor

Para calcular la aproximación de la función seno usando expansiones a través de serie de Taylor, necesitamos un punto, el cual para este caso usaremos x₀ = 0 y n derivadas de la función, como la función seno es de continuamente diferenciable, entonces no tenemos problemas para construir la aproximación a través de una serie de potencia.

Así, entonces podemos expresarla de la siguiente manera:

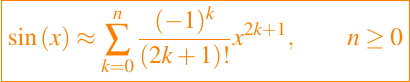
por lo tanto podemos tomar diversas aproximaciones con diferentes ordenes, para nuestro estudio, usaremos 5 aproximaciones, que son las primeras 5 sumas parciales de la serie de potencia mostrada anteriormente, pero debemos aclarar que la primera aproximación solo es una buena aproximación cuando los ángulos a evaluar son suficientemente pequeños, es decir, para valores entre 0 y 1, dicha aproximación es muy buena. Sin embargo, la tomaremos en cuenta para nuestro objetivo acá.


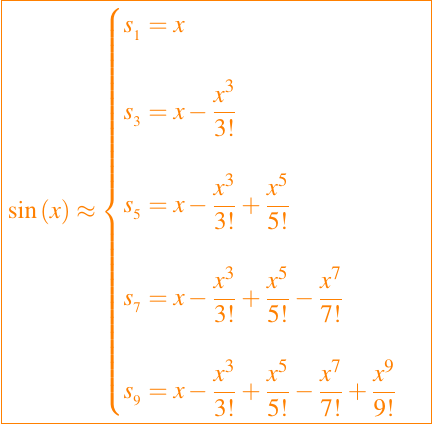
las cuales al desarrollar los factoriales del denominador obtenemos

---

---

Cálculo del Error de las Aproximaciones

Para el cálculo del error de las aproximadas dadas anteriormente, usaremos tres medidas, la primera es el cálculo del error relativo de cada aproximación, el cual lo calcularemos de la siguiente manera:

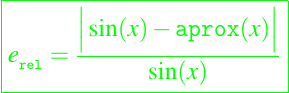
La segunda medida es la conocida como la norma del máximo, dada por:


La tercera medida que usaremos es la norma L², la cual mostraremos en su forma continua y su forma discreta, dadas a continuación:

---

---

Implementación Numérica

Para la implementación numérica, usando las aproximaciones de la función seno dadas por la aproximación de Bhaskara I, las aproximaciones de sumas parciales de la serie de Taylor, para ello he escrito un script sencillo donde se puede observar la forma de realizar los cálculos, usando el entorno GNU Octave, el cual muestro a continuación:

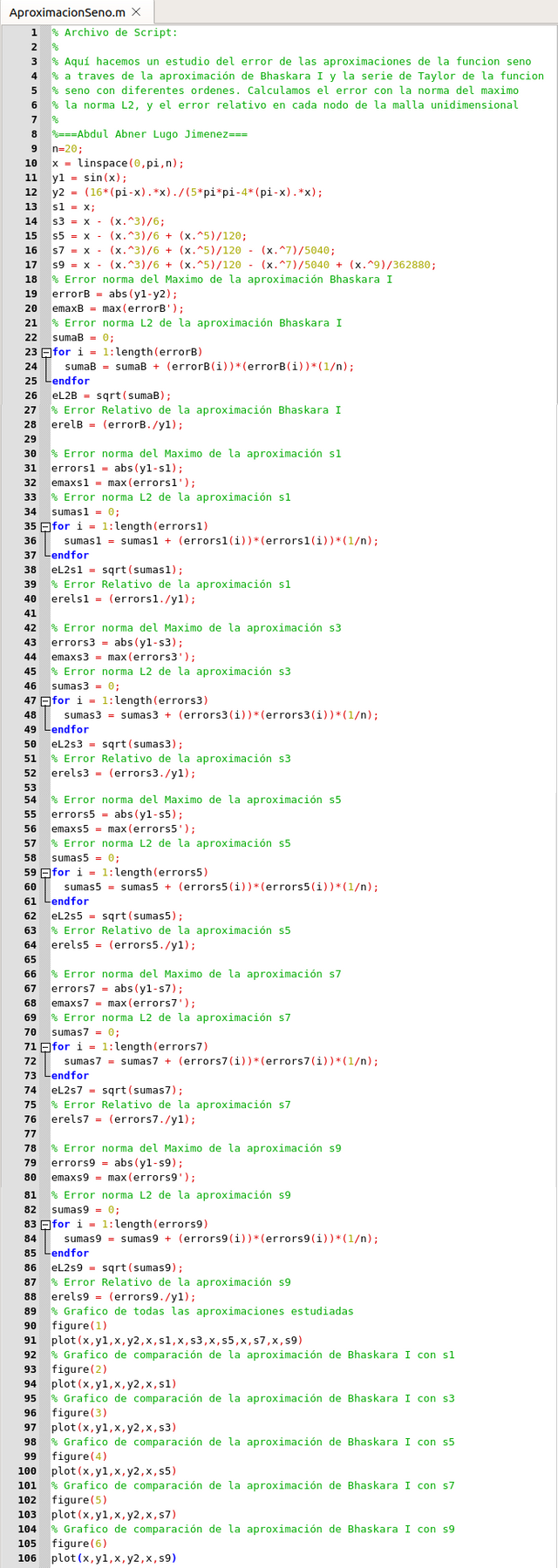
_{Script para la implementación de las comparaciones numéricas de la función seno con las diferentes aproximaciones. Elaborado por @abdulmath.}

El siguiente gráfico mostramos los trazos de la función seno con sus aproximaciones, en el podemos apreciar que en algunos casos se pueden estar solapando la función seno con alguna de las aproximaciones.

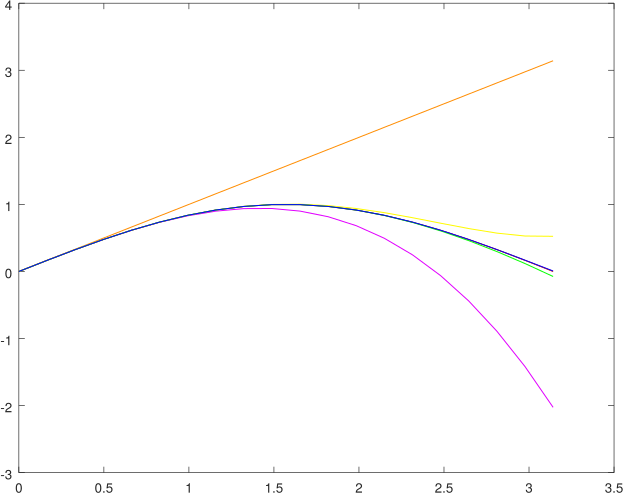
_{Gráficas de la función seno y las aproximaciones. Elaborado por @abdulmath}

Es por ello, que a continuación mostraremos una serie de gráficos, donde mostraremos la función seno con la aproximación de Bhaskara I y una de las aproximaciones por serie de Taylor comentadas ya anteriormente con el fin de ir viendo la evolución de las sumas parciales de la serie de Taylor.

El primero que describiremos es el gráfico de la función seno y la apoximación de Bhaskara I, como podemos apreciar, visualmente pareciera que solo tenemos una sola línea de gráfica, pero cuando hacemos un zoom en el grafico en cualquier parte, podemos apreciar como no son la misma línea, pero sin embargo hay una buena aproximación de la misma, en color rojo tenemos a la aproximación de Bhaskara I y en color azul la función seno.

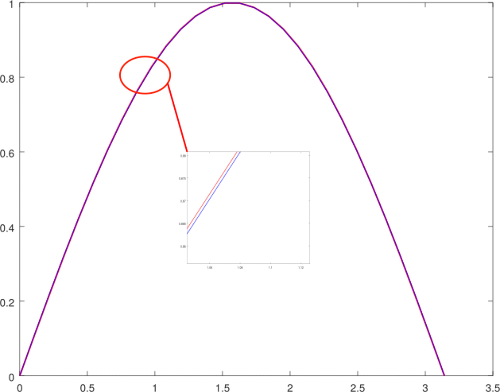
_{Gráfico de la función seno vs la aproximación de Bhaskara I, con un detalle de un zoom en una zona de la gráfica. Elaborado por @abdulmath.}

En vista de la situación vista anteriormente, la serie de gráficos que mostraremos a continuación, será la aproximación de Bhaskara I versus las sumas parciales de la serie de Taylor de diversos ordenes.

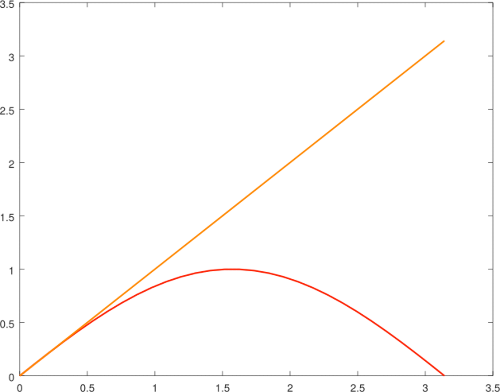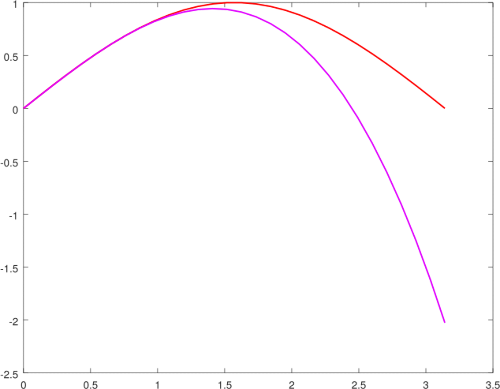Aproximación de Bhaskara I versus s1.	Aproximación de Bhaskara I versus s3.
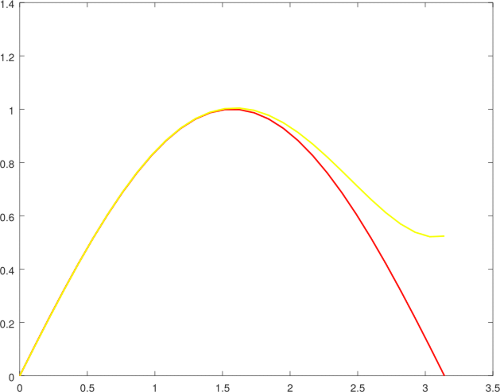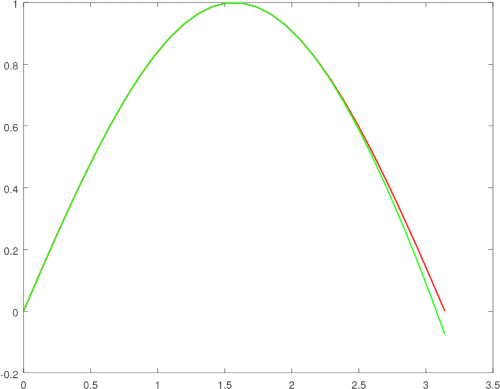Aproximación de Bhaskara I versus s5.	Aproximación de Bhaskara I versus s7.

Hasta podemos observar que las aproximaciones sumas parciales de la serie de Taylor para la función seno, se ha ido adaptando y acercando a sus valores exactos, incluso las hemos comparado con la aproximación de Bhaskara I y cada vez que aumentamos el orden, se aproxima mucho más, a continuación mostraremos la última comparación gráfica, y hemos tenido que hacer un zoom cerca de la frontera derecha.

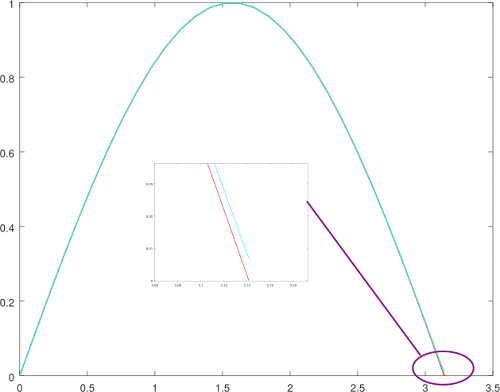
_{Aproximación de Bhaskara I versus s9.}

---

---

Resultados Numéricos

Ahora bien, ya que hemos visto gráficamente la comparación de las aproximaciones de la función seno, veamos ahora en números como van dichas aproximaciones. Es decir, en las siguientes tablas que mostraremos a continuación veremos como los números nos dirá que aproximación va bien, en el dominio que estudiamos.

La primera tabla que presentare, es donde resumimos los resultados de cada aproximación con la norma del máximo y la norma L².

Aproximación	Error Norma del Máximo	Error Norma L2
Bhaskara I	0.0015912	9.4437x10-04
s1	3.1416	1.3985
s3	2.0261	0.70114
s5	0.52404	0.16006
s7	0.075221	0.021231
s9	0.0069253	0.0018504

En la siguiente tabla mostraremos el error relativo en cada nodo de evaluación de las aproximaciones estudiadas

	Bhaskara I	s1	s3	s5	s7	s9
x1	0	0	0	0	0	0
x2	3.3431e-03	2.0600e-02	1.2591e-04	3.6571e-07	6.1926e-10	6.8638e-13
x3	1.4838e-03	8.6100e-02	2.1252e-03	2.4781e-05	1.6814e-07	7.4599e-10
x4	1.3401e-03	2.0920e-01	1.1806e-02	3.1163e-04	4.7714e-06	4.7707e-08
x5	1.9534e-04	4.1780e-01	4.2877e-02	2.0290e-03	5.5453e-05	9.8792e-07
x6	1.9534e-04	7.7225e-01	1.2751e-01	9.5303e-03	4.0909e-04	1.1421e-05
x7	1.3401e-03	1.4184	3.4965e-01	3.8128e-02	2.3717e-03	9.5682e-05
x8	1.4838e-03	2.8014	9.8131e-01	1.4791e-01	1.2616e-02	6.9561e-04
x9	3.3431e-03	7.1648	3.4470	6.9065e-01	7.7593e-02	5.6146e-03
x10	1.0000	2.5653e+16	1.6545e+16	4.2791e+15	6.1422e+14	5.6549e+13

Luego, analizando los resultados numéricos, podemos observar que como dije al principio, la aproximación de Bhaskara I es una aproximación impresionante, excepcional, y única. En cuanto a su precisión, digamos que es muy buena, incluso mejor que las aproximaciones estudiadas de las sumas parciales del desarrollo de la serie de Taylor de la función seno. Desde el punto de vista computacional, es una aproximación que uso menos recursos de memoria en la computadora, ya que necesita realizar menor cantidad de operaciones. Para finalizar, si necesitan una aproximación de la función seno entre 0 y pi, pues les recomiendo usar la de Bhaskara I por los motivos antes expuestos y muchos otros los invito a ir descubriendo si aplicamos la misma.

---

---

Queridos amigos y lectores, espero hayan disfrutado de esta publicación, al igual que yo disfrute mucho realizando la misma y disfrutando la belleza que nos brinda la matemática y apoyándonos con herramientas computacionales para descubrir y resaltar temas de tanto intéres. Estoy seguro que será de mucho apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

1. Bhaskara I - Wikipedia, la enciclopedia libre.
2. Bhaskara I - MacTutor History of Mathematics archive.
3. Björck, Åke. Numerical methods in matrix computations. Vol. 59. Cham: Springer, 2015.
4. Burden, Richard L., and J. Douglas Faires. Numerical analysis. Ninth Edition. Cengage Learning. 2011.

---

La imagen del inicio, fue tomada del Twiter de Fermat's Library, editada con GIMP por @abdulmath. Los separadores y ecuaciones fueron creadas y editadas por @abdulmath usando software libre, GNU Octave, , GIMP e Inkscape.

---

---

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

_{Imagen diseñada con GIMP y elaborada por @abdulmath.}