Mr Sandman and Mr Upside-Down in Action
I have introduced Mr Sandman and Mr Upside-Down in an earlier article.
In this article, I shall illustrate integer arithmetic with more examples. Remember that what our Sandman calls a “hole” is a “mound” to Mr Upside-Down.
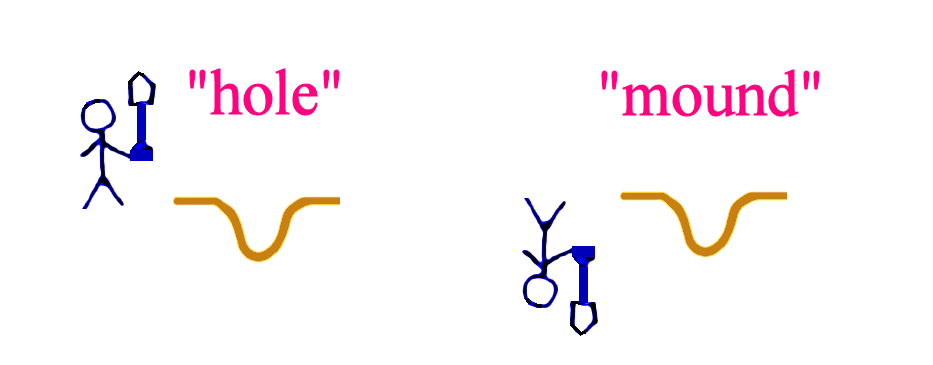
Whenever we have a whole (i.e. mound) and a hole, they cancel in the sense that we can use the sand from the mound to fill up the hole and we get level ground (i.e. 0).
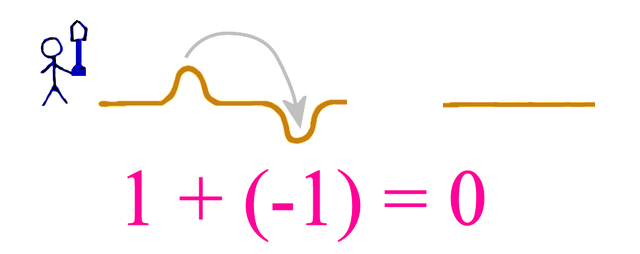
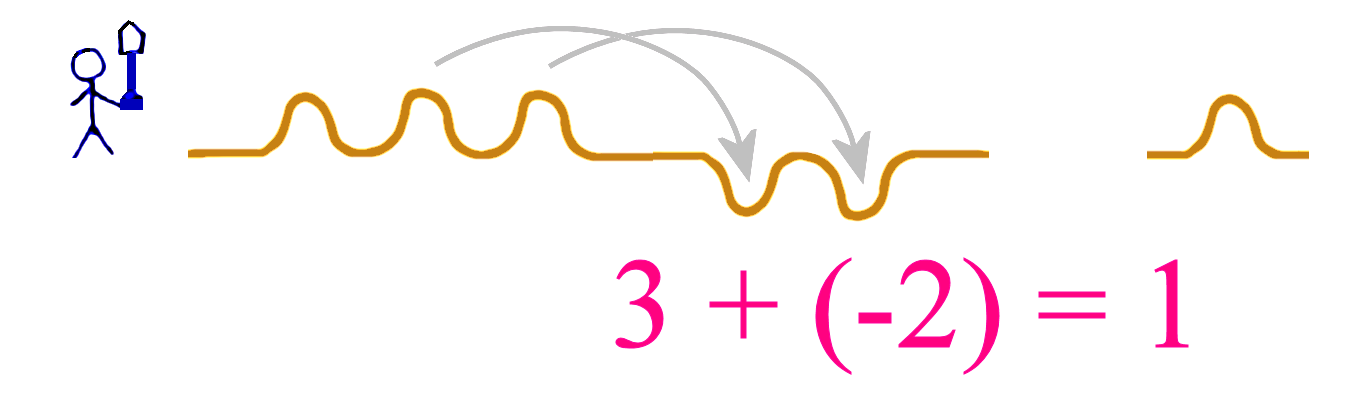
If we have 3 mounds and we add 2 holes, then we use two of the mounds and fill up the holes, and we are left with 1 mound.
You will notice that this is the same result as if we had 3 mounds and then we removed 2 of the mounds. 1 mound remains.
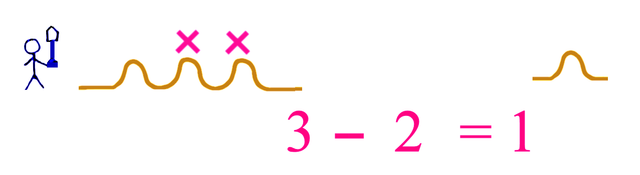
If we start with one hole (-1) and we get Mr Sandman to dig (– ) two holes, then we get 3 holes, so -3.
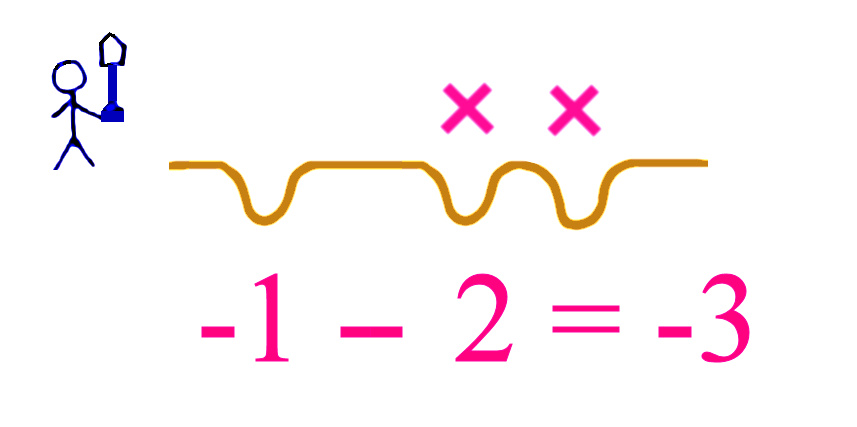
But if we start with one hole (-1) and we get Mr Upside-Down to dig (– ) two of his “holes” (so he is subtracting -2), then we actually get two real mounds. So this is really like adding 2. After levelling our original hole with one of the mounds, we are left with 1 mound. So -1 – (-2) = -1 + 2 = 1.
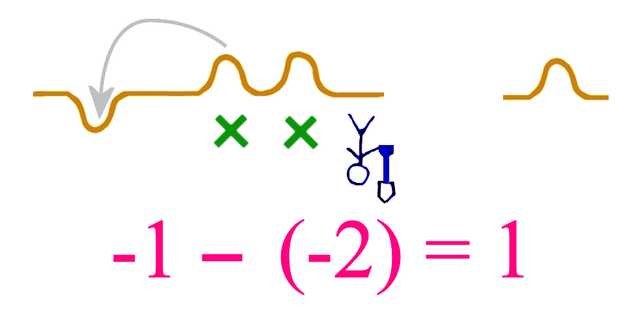
I hope you have enjoyed my presentation and learned something.
This post recieved an upvote from minnowpond. If you would like to recieve upvotes from minnowpond on all your posts, simply FOLLOW @minnowpond