Euler's Genius makes Complex Numbers easy
Leonhard Euler (pronounced “oiler”) (1707 - 1783) was not a ruler, but he put lots of oil into mathematics. He was the Beethoven of maths. As you know Beethoven was deaf, but he could compose music. Well Euler was almost totally blind , but he was one of the most prolific mathematicians. He wrote many papers that solved mathematical problems. He discovered mathematical theorems, and even invented new mathematics, e.g. graph theory. He fiddled around with the Maclaurin series of sine, cosine and exponential functions on real numbers, which have similar patterns.
He noticed that if he substituted an imaginary number instead of the real number x, he could link the exponential function with the trigonometrical cosine and sine functions via his beautiful formula
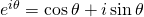 . This ties together many trigonometric formulas elegantly. Resolving as real and imaginary parts of
. This ties together many trigonometric formulas elegantly. Resolving as real and imaginary parts of , we can think of the cosine and the sine as "shadows" of
when light is thrown at it from different angles.
The verbose expression 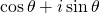 , sometimes artificially abbreviated as cis
, sometimes artificially abbreviated as cis , just contains information about the angle
. Via Euler’s Formula, we can repackage the information naturally in a compact form as
.
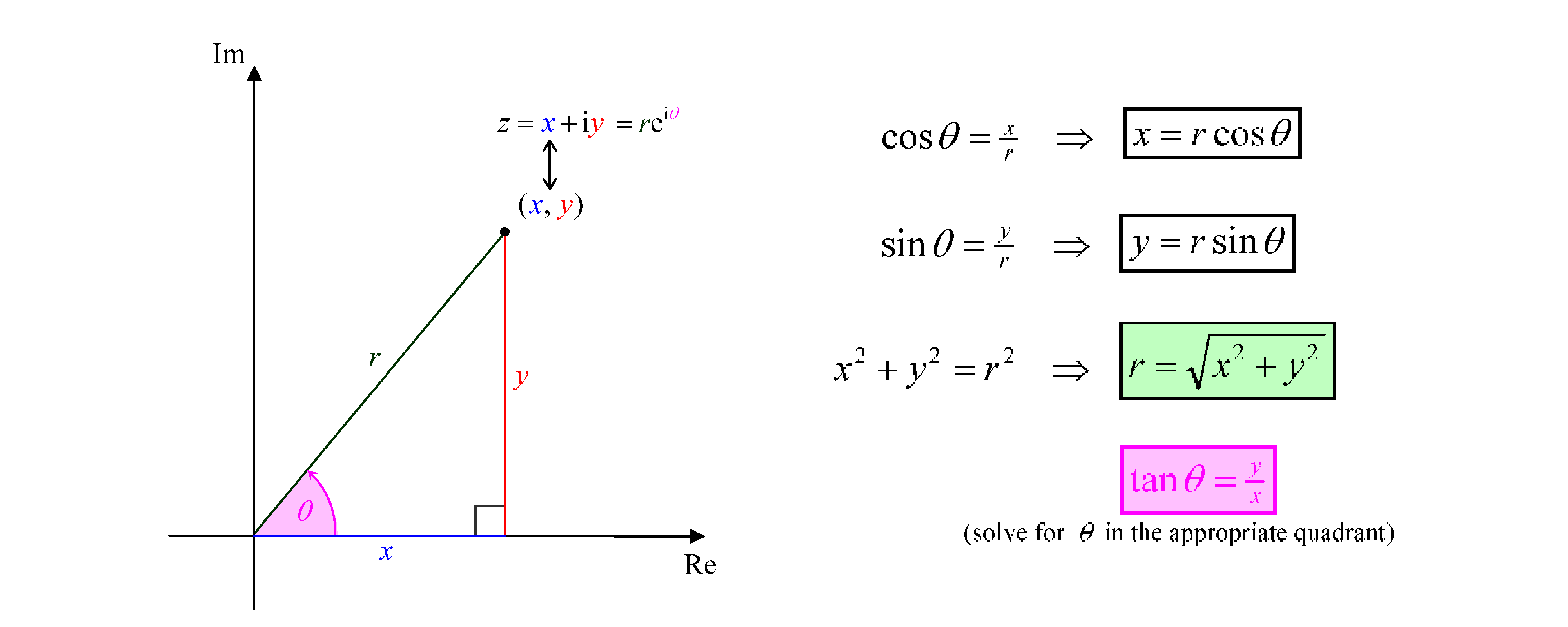
Every complex number z = x + i y, represented by a point Z(x, y) on an Argand diagram, can be expressed succinctly as , where r is the "modulus" or distance of the point to the origin O and
is the “argument” or anti-clockwise angle turned from the positive real axis (x-axis) to the vector
. Clockwise angles are treated as negative.
If we let the modulus be 1, and the angle be radians i.e. 180 degrees, we get -1.
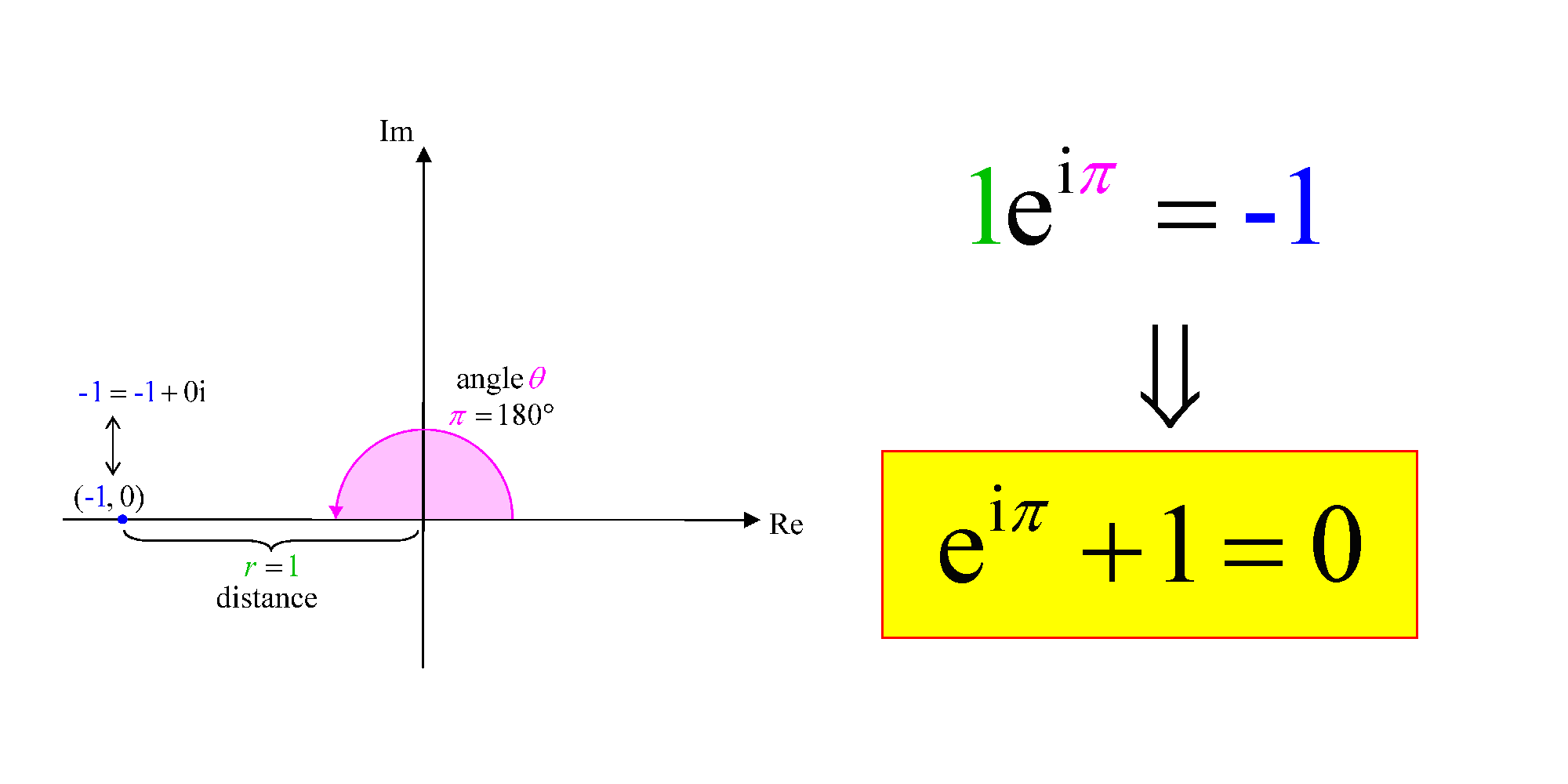
In other words, . Rearrange that, and we get the equation
.
This is said to be the most beautiful equation in mathematics. It brings together the five most important constants in mathematics, namely e, i, , 1 and 0. You must remember that these five entities are strange bedfellows. The rational integers 0 and 1 like to tell the irrational numbers
and e: “Be rational!”. But
and e are not only irrational, they are transcendental. Maybe they like to practice Transcendental Meditation. And these four guys like to get gang up against the imaginary unit i and tell him to “Get real!”. So how can these 5 guys can ever work together? And yet they do, by Euler’s magic!
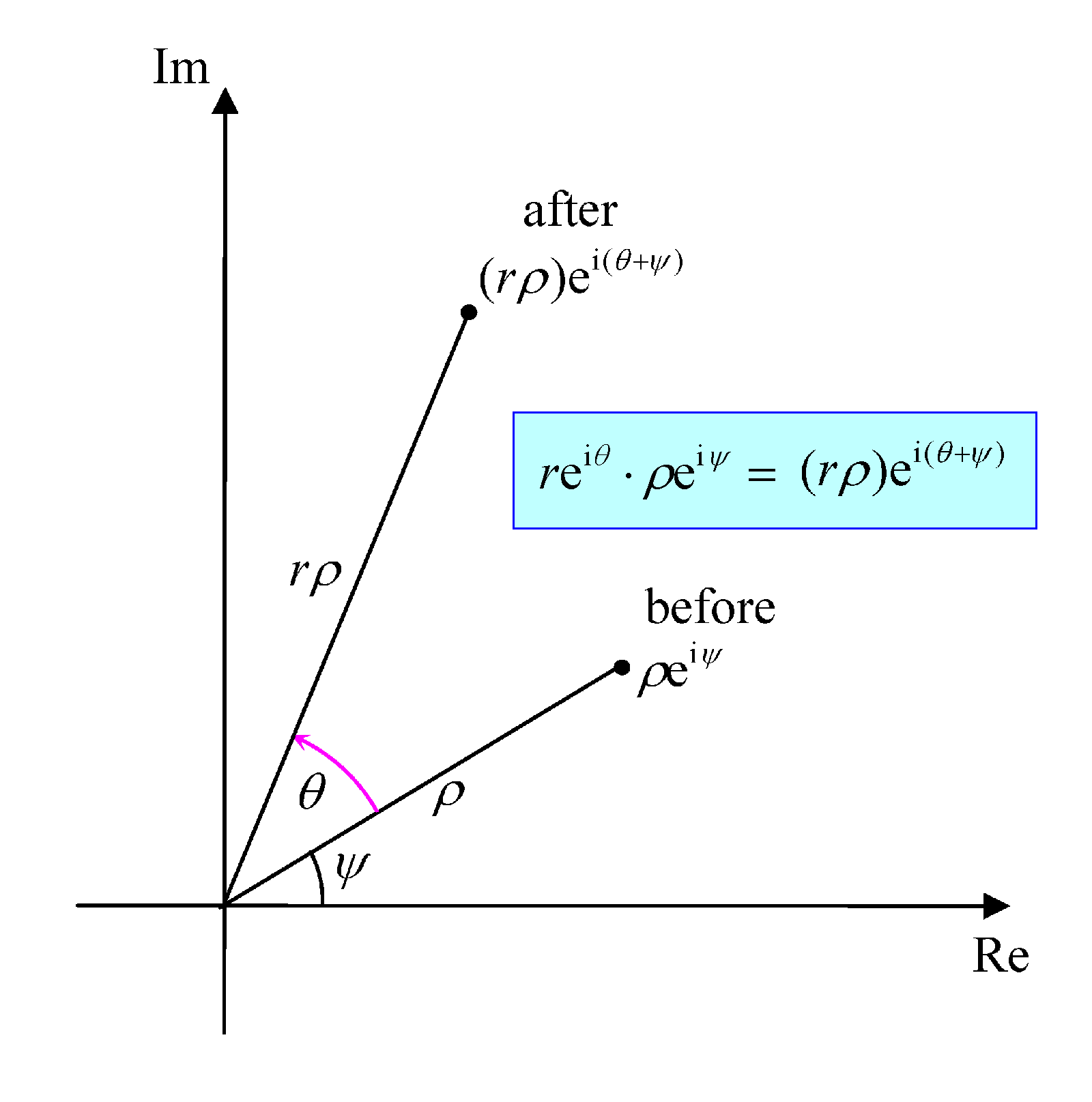
From Euler’s formula, we can easily appreciate that when we multiply the complex number with the complex number
, we will get
. In other words, the moduli (distances from the origin O) get multiplied together to give
, while the angles get added together to give
.
Thinking in terms of tranformations, when the complex number is multiplied by
, it gets radially stretched by a factor of r with O as centre (they call it a “homothety”), while being rotated by a clockwise angle of
, again with O as centre. If it were a division, the modulus would be divided by r and the angle subtracted by
. When r = 1, there is no stretching, and it is just a pure rotation.
Some of you may have heard of De Moivre’s Theorem. Wait! How do you pronounce that French mathematician’s name again? It is like “dee mwavR”. The “vR” sounds as hot as "poivre" (pepper) and as awe-inspiring as Louvre (the museum), but to many students, De Moivre’s Theorem sounds like de-moral-ising theorem. The formula looks soooooo long and unfriendly.
However, if you understand the idea behind it, it will make you and Mona Lisa smile. Powers are just repeated multiplication, and using the above idea of pure rotation when r = 1, raising a complex number with modulus 1 to some power simply means rotating the thing to several times its original angle. For example, if , then
. The original angle of 45 degrees has been multiplied by 3 to get 135 degrees, but the distance from O remains as 1. We can easily work out the coordinates, but the main idea is: the power of a unit-modulus complex number means a rotation by some number of times.
We can generalise this. Using Euler’s formula, if we raise to the power of n, we easily get
. This is just de Moivre’s Theorem in a compact form! The rotation just multiplies the original angle
by n to give
and the complex number remains on the unit circle.
As you can see, understanding the ideas of rotation and stretching is very useful for dealing with multiplication, division and powers of complex numbers. Euler’s formula not only made de Moivre’s Theorem less demoralising, it gives a compact form for complex numbers. It links together sine and cosine and allows trigonometry to be seen in a new light.
I hope with this article, you understand something about the power and beauty of complex numbers and mathematics via Euler’s genius!
P.S.: All the diagrammatic illustrations in this article are my original work. As suggested by @lemouth I have included some external references. I have included them as embedded hyperlinks. So just click on the highlighted terms to find out more about them. This video has shows some very interesting animation of the stretching and rotation concept, starting from around the 10 min 30 sec mark.
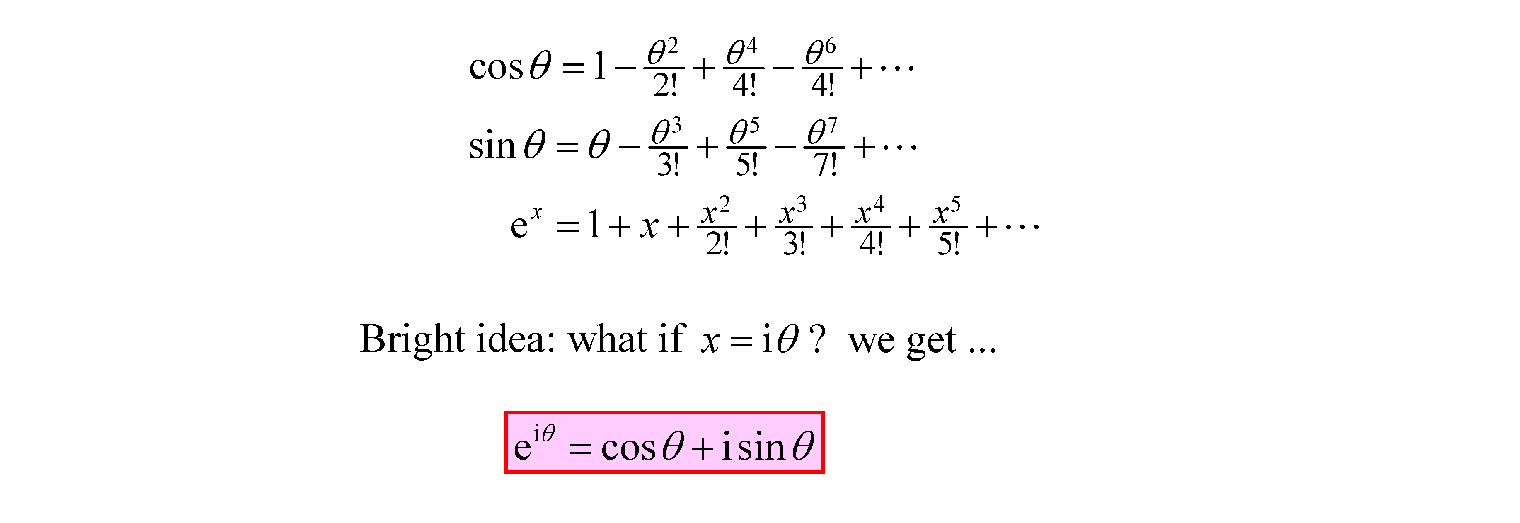

Hi,
That is a very interesting post. I think it would be very useful, for the readers, to add extra references where more information could be found. In addition, I am fully convinced this will bring you more rewards ;)
Thanks in advance for your consideration.
Thank you @lemouth very much for your support and your suggestion. I'll put in some links.
:)
Please make sure to state your resources.
All the colorful diagrams are my original artwork, painstakingly done. Although the ideas contained in this article contained in many books and websites, the way I present the ideas is my original work, and this is only possible through deep understanding and digestion after years of learning, thinking and teaching of the material. External references provided as hyperlinks, if the reader wants to know more about the particular terms.