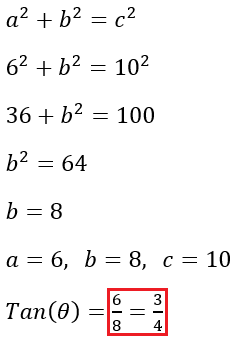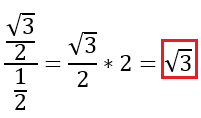Solution to SAT Math Practice 1

Graph the function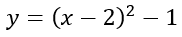
From last time, we know that there is a shift to the right 2 and a shift down 1. The graph is our answer:

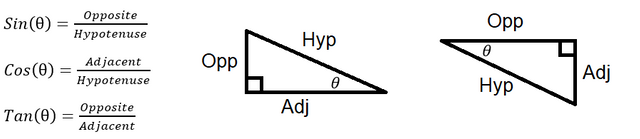
Basic Trigonometric Ratios

These are best known by high schoolers as SOH CAH TOA. It is better to know and understand the equations of course...

Memorize this and know that not all right triangles look the same. It is easy enough to find the correct orientation of sides given the angle. Just remember that the hypotenuse is the longest side always across from the right angle (90 degrees).

Creating the Unit Circle with GIFs

30, 60, 90 Triangles

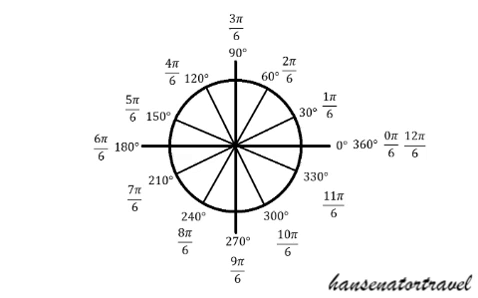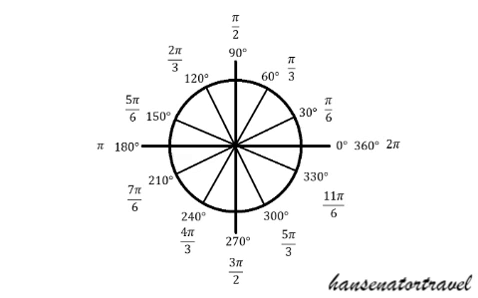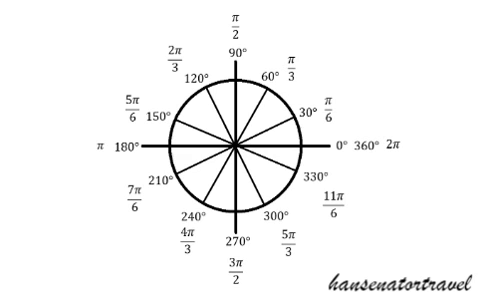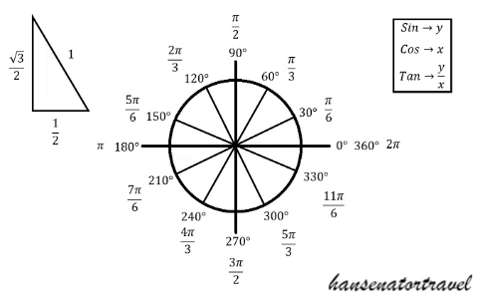
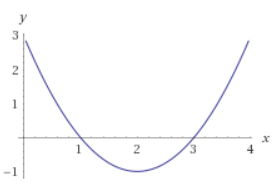
Notice that in both of the unit circles we are counting 0, 1, 2, ... from the +x-axis to create the measures with pi. To answer questions, say Sin(30 degrees) or Sin(pi/6), we will look at the y-value created by the triangle for that angle. Remember that the longer leg of the 30, 60, 90 is sqrt(3)/2 and the shorter leg measures 1/2. Therefore Sin(30) = 1/2.

45, 45, 90 Triangles

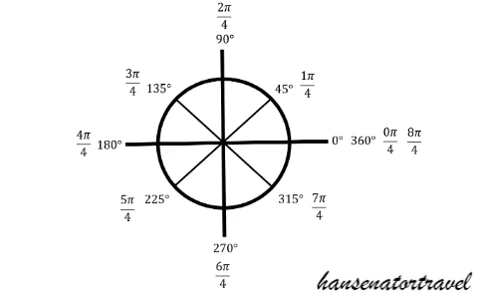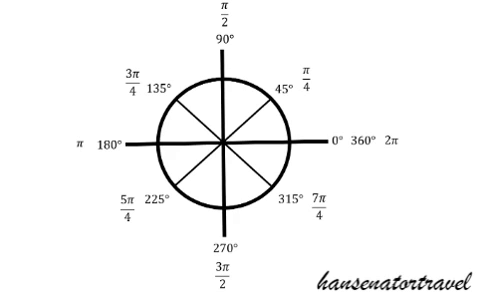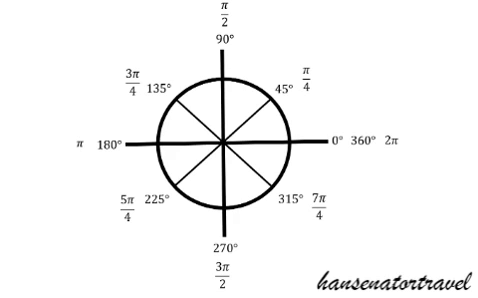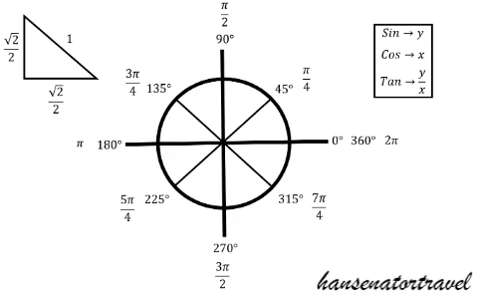
The signs, positive or negative, matter as well. For example, Cos(3*pi/4) = - sqrt(2)/2 because it is on the negative side of the x = axis.

Examples

1. A triangle has the trigonometric ratio 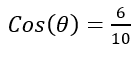. Find .
   
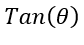2. Using the unit circle above, find Tan(120 degrees).
   
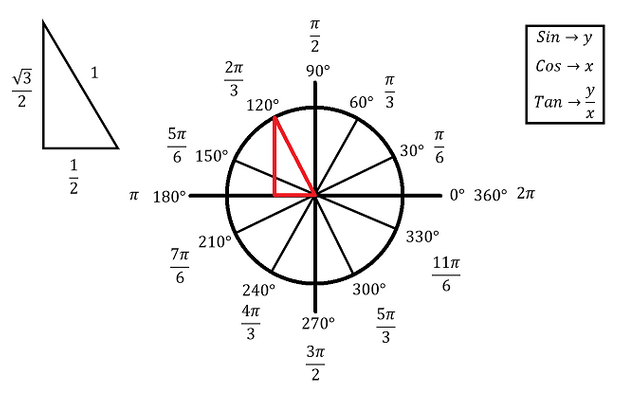
   Remember that Tangent is equal to y/x, so the answer is
   
3. Find Sin(300 degrees).
   Sin is y and we see that it is the longer side in the negative direction, so the answer is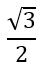
   
   
   
   Learn for Steem! Happy Trails & Best Wishes my friends!