Actuary Exam P1 Practice

Law of Total Probability

Let the sets 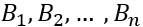compose a partition of S. Let A be an event. The sets 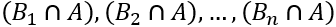, formed bu intersecting A with each of the B's, compose a partition of A. Then,

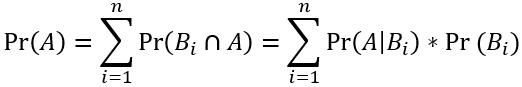
Example

The CDC is tracking a virus in 3 cities because they know exactly who is infected. In any of the given towns, the probability a person is infected is:

Pr(Albany) = 25%, Pr(Orlando) = 40%, and Pr(Montgomery) = 35%

Let A be the event that someone dies. The CDC measures the following:

Pr(A|Albany) = 60%, Pr(A|Orlando) = 20%, Pr(A|Montgomery) = 28%

What is the probability of death of a single person?
We have to use the law of total probability, so

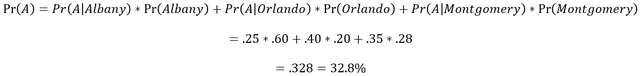
This makes sense because the probability of someone dying in Orlando is the probability that they are sick times the probability that they die in Orlando. Add up all three and you have an estimated death toll. Morbid, but useful. Haha.

Bayes' Theorem

Suppose that set B contains an possible events labeled 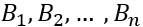. All the B events must be disjoint, and they partition S. Let A be another event with positive probability. Then,

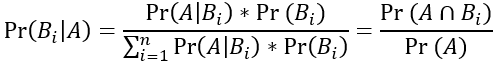
Example

A deck of cards has
3 purple (P) cards labeled 1-3
5 orange (O) cards labeled 1-5
8 yellow (Y) cards labeled 1-8
You draw a card and the value is greater than 2.
What is the probability for each card color?
First, we need to know the probability of drawing each card color because we need Pr(Bi).

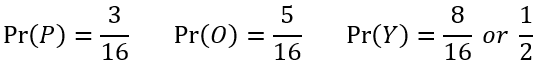
We already are given the probabilities of the number of each color as well. Let A be the event that the number is over 2. For example, the probability of drawing a number over 2 for purple is 1/3 because the set is {P1, P2, P3}.

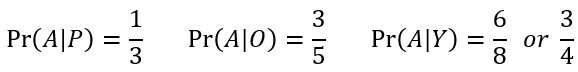
Now, we can calculate the probability that A happens, then that is our total (denominator).

Being able to understand what the equations are saying by reading them is the most important thing when learning this. It takes me a few times just to remember why it works, but that is how you know when to use it!



Thank you for coming back! Learn Much & Best Wishes!