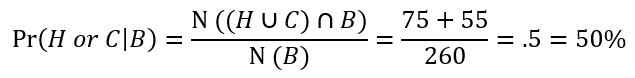Actuary Exam P1 Practice

Actuaries don't do a lot of math on the job because of software nowadays, but it is still a great career to get into because of the pay! If you are decent at math, then you can do it! Just study this set of tutorials. You only need to pass one test to be eligible for a job!

Independent Events

Independent Events are disjoint events that can not be related to each other, but we can still view them as a Venn Diagram if necessary. Believe me if you have four events with mixed independent situations, it can be tough.

Theorem for Intersection if Independent Events

Events A and B are independent iff (means if and only if) .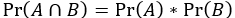

Example 1

Tom (T), Dick (D), and Harry (H) watch the news rarely on a daily basis and independently of each other. The probability each watch the news on any given day is Pr(T) = .05, Pr(D) = .15, and Pr(H) = .12.

What is the probability Tom and Harry both watch the news today?

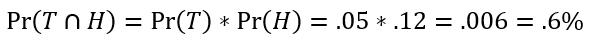
What is the probability that all three of them watch the news on any given day?

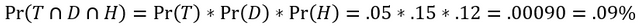
Example 2

A store has a bowl of jelly beans with 6 red jelly beans and 8 blue jelly beans. A child wants to pick out 5 jelly beans randomly one at a time.

What is the probability that he will pick 5 blue jelly beans?
Since the child is picking independently we can use the probabilities separately and multiply for each pick. The total decreases each time by one because 1 jelly bean is lost each pick.

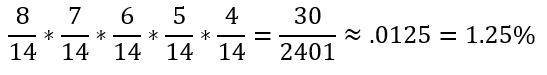
What is the probability that he will pick 4 red and 1 blue?
The tricky part of this one is that there are 5 ways to do this. For instance, you can pice 1 red 1 blue then three red... or you can pick 1 blue and 4 red. Thus, we have to multiply our answer by 5. This is actually called a combination, something we will be getting to soon.

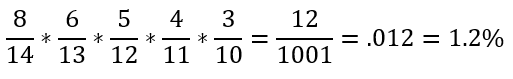
Conditional Probability

If events are dependent and have a probability of both happening we can do more if we know that one of those events happened. The formula for conditional probability is:

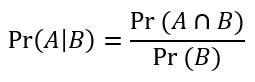
It is read like "The probability of A given that B already happened is equal to the probability of A and B divided by the probability of B". Read that over a few times if you don't already understand it. If A and B are independent, then the formula becomes:

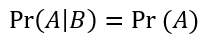
beacause B no longer matters.

Example

Consider an insurance company that has two plans for each of their policies. The number of people enrolled in each policy is given below.

What is the probability that they have car insurance given that it is plan A?

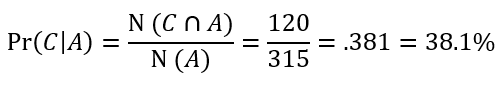
What is the probability that they are on plan B given that they have Home insurance?

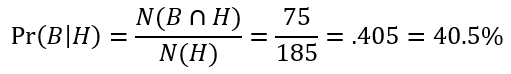
What is the probability that they have Home or Car insurance given that they are under plan B?

Thank you for everything Steemiteers! Keep adding to our encyclopedia of knowledge!