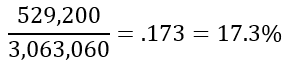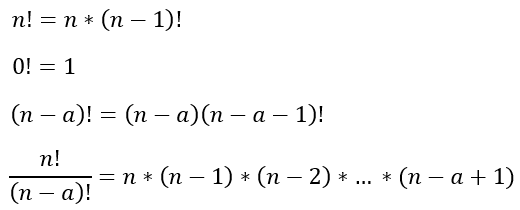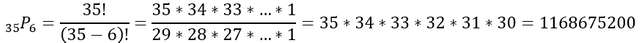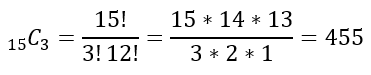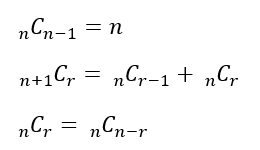Actuary Exam P1 Practice

Counting principles have always been a favorite of mine. When I taught Algebra I would always show the kids a few cool examples. Here is what you need to start. It's not hard at all!

Counting Principles The Basics of Combinatorics

Factorials

In mathematics, the factorial ( ! ) just means multiply all the way down to 1.

For example, 5! = 5*4*3*2*1

Properties of Factorials

Basic Counting

I love this because of how easy it is. Think of it this way, you have n spots to fill with the number of choices you have to fill it, then multiply all of the numbers. The answer you get is the number of total possible outcomes.

Example

Students like to guess on True/False exams, so I show them this example. On a 10 question quiz that is all True or False, how many different sets of answers can you get?

Two to the 10th power is 1024. With this answer we can find much more about the problem too.

Permutations and Combinations

Permutation Example

License plates in Florida generally have 6 letters and/or numbers. This includes A-Z (26 letters) and 1-9 (9 digits), so that is 35 objects total.
How many possible license plates can there be?

Clearly, there are enough possible for the population. Haha.

Combination Example

There are 15 mice in a cage and a child wants to pick 3 of them out. How many different sets of mice can be chosen?
Here order doesn't matter because if the child picks {mouse 3, mouse 4, mouse 10} or {mouse 4, mouse 10, mouse 3}, there's no difference.

Combination Properties

Example

A teacher must divide 20 students into two groups. Group 1 has 8 people and Group 2 has 12 people. Jim and Rachel are friends and they want to be put in the same group. What is the probability that they end up in the same group?

First we have to find the total number of groups that can be made, then we find the number of ways that they can end up in both groups.

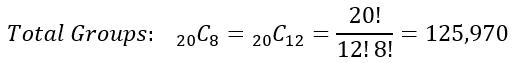
Now is the tricky part. Finding how many ways they can be put in Group 1 and 2. Since we know they end up in the group together, we chose from 18 students for each group size minus 2 because they are in the group already.

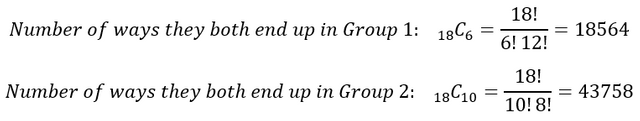
So our answer is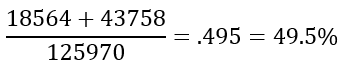

Multinomial Combination

We use this to beak up a group into several smaller groups. We actually used it in the last problem without knowing it when we found the total number of groups possible, but since there were only two groups we didn't need the formula.

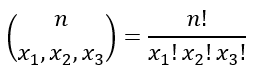
You can do this for however many groups you need. Also know that the bottom adds up to the top.

Example

There are 5 red rooms, 8 blue rooms, and 4 green rooms in a hotel. Nine people want to stay the night. What is the chance that 3 stay in a red room, 4 stay in a blue room, and 2 stay in a green room. The other rooms are unoccupied.
First we find the total number of ways that the rooms can be ordered:

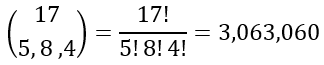
Then we multiply the number of occupied rooms times the number of unoccupied rooms. Since we know what we want we can build the scenario with two more multinomial combinations.

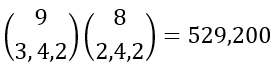
Then divide the two outcomes!




Thank you for stopping by! Have a great day!