Chapter 7 - Risk Measurement I

The Vega K

Vega, otherwise known as kappa (K) since there is no Greek letter Vega, is the change in volatility. More specifically, it is "the change in theoretical value for each one percentage point change in volatility".

For example, if our measure of Vega is .20, then for every 1% volatility change we can expect the underlying price to change .20 in the same direction as the volatility. Remember that the higher the volatility the higher the value of the option.

Another example, if an option has a price of 1000 with a Vega of 40 and a volatility of 25%, then it will have a theoretical value of 1080 if the volatility rises to 27%. We can make a simple equation for this...

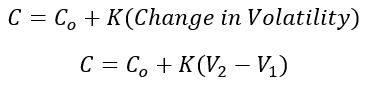
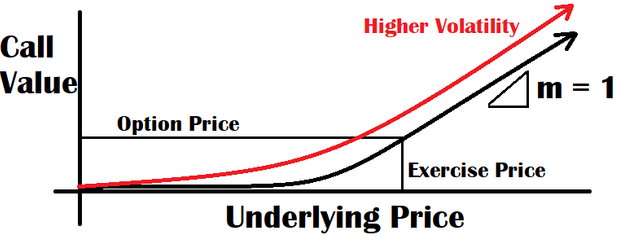
The Rho P

This is the change in theoretical value for each one percent change in interest rate.

From an option trader's point of view, there is no change in the underlying for a change in interest rate (Futures-Type Settlement).

For an underlying contract, we know that the Delta is 100, this means (since delta is constant) that Gamma, the change in delta, is 0. The underlying contract does not depend on time, so Theta is 0. Last, it does not depend on volatility or interest rates, so Vega and Rho are 0. Thus we can use these for options only, calls and puts.

Interpreting Risk Measures

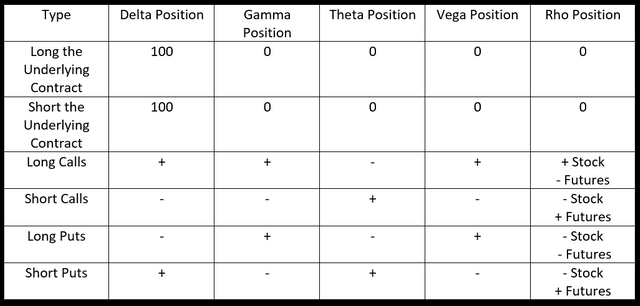
• For a Futures-Type Settlement, Rho will always be 0.

Natenburg gives this table a few pages later, but I think it is more useful now and we can refer to it. To describe the figure above.

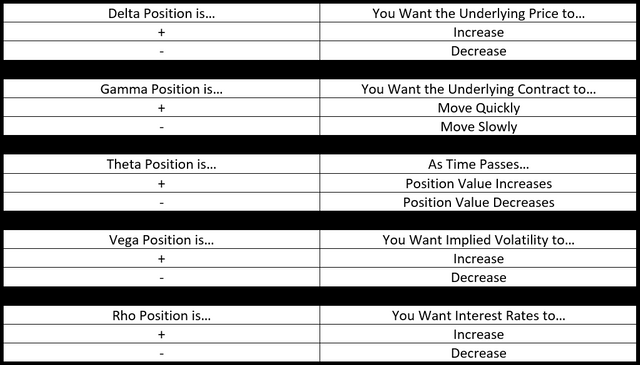
Example

Given the following values, we will describe each of the variables and how the trader analyzes them.

We can construct the following to tell us what we want for this particular situation.

1. We always want our theoretical edge to be positive. If it is negative, get out!
2. Delta is barely negative, but we want the market to fall because of it.
3. Gamma is negative, so the market should move slowly.
4. Theta is positive which means over time the option will be worth more. Money is made here.
5. Vega is negative, so we want the volatility to decrease.
6. Rho is negative, so we want the interest rates to decrease which makes sense because the long stock position will dominate the cash flow, resulting in a debit.

We can make these examples more complicated, like 2 calls and a put, but we just do the same thing to calculate the Greeks.

Source:

Natenberg, Sheldon. Option Volatility and Pricing Advanced Trading Strategies and Techniques. 2nd ed., McGraw-Hill Education, 2015.

Hope you've enjoyed today's lesson! Happy Trails & Best Wishes!