Quantum computing and cryptocurrencies: Are Steemit and bitcoin safe?
What is quantum computing?
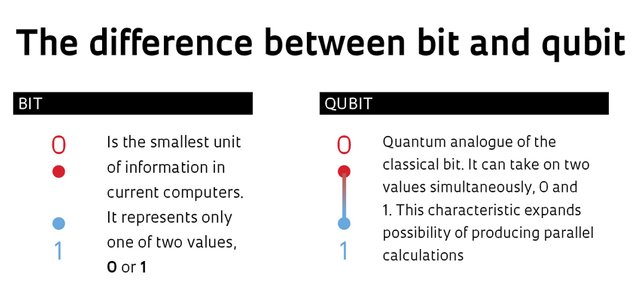
In a classical computer bits are used that can either be 0 or 1. In a quantum computer these bits are replaced with Qubits (quantum bits). These Qubits can be 0 or 1, or both at the same time. This is caused by a phenomenon in the quantum realm called superposition. At scales the size of an atom and small molecules, the spin of particles is not determined until it is observed.A pair of Qubits can be in any quantum superposition of 4 states, and three Qubits in any superposition of 8 states. In general, a quantum computer with n Qubits can be in a superposition of up to 2^n different states simultaneously (this compares to a normal computer that can only be in one of these 2^n states at any one time). Because of this, a quantum computer is able to perform computations at the same time, while classical computers perform computations one at a time.
This effectively means that the computing power grows exponentially for each Qubit you add to the system. A quantum computer will be able to make really difficult calculations all the classical computers in the world together would not be able to do before the end of times, in a relatively short amount of time. This opens to world of computing to be able to perform amazingly complex calculations, such as weather or large scale quantum mechanics, with extremely high precision. Unfortunatly, it will also be great at cracking certain types of cryptography.
Bitcoin and quantum computing
A quantum computer would be able to decuce the private key from a public key. If a bitcoin adress has never been used before, the bitcoins inside would be safe because the public key would not be known. The problem is, how do you make a safe transaction? A bitcoin transaction must include a signature and a public key to ensure that it was the owner of the corresponding private key who made the transaction. When you make that transaction, all information a quantum computer needs to get the private key will be released to the public. This would enable the quantum computer to impersonate you and send other transactions from the same adress.
For example if you make a transaction spending all 100 BTC in adress (A) with 30 BTC going to adress (B), to pay for goods, and 70 BTC returning to your own, new adress, (C). The first node you send the transaction to can change to return adress to their adress (D), get your private key, forge your signature and steal your BTC. The way to get around this would be to send your transaction directly to a trusted mining pool and have them include it directly in the blockchain. But then you would still be vulnerable to a Finney attack.
The solution
Lamport signatures. These one-time signatures are effectively unforgeable. It would take a quantum computer 2^80 steps to create a fake transaction in which they have to reveal the same private you have already revealed. Or it would have to take 2^(80*80) steps to try all the possibilities. Both numbers are too big, even for a quantum computer. The only change that would have to be made besides Lamport signatures, is that people should use an adress only once. because when you use it a second time, that number will drop to 2^40. In three uses it would fall back down to the amount of security we have today.
Conclusion / TL;DR
Eventhough quantum computing is coming closer and closer within the reach of humanity every day, it's still not quite there yet. Quantum computing will form a problem for bitcoin as it is today, but there are relatively small measures we can take to overcome that. It is time to start thinking about implementing these measures, because we can't know for sure how far we really are in achieving quantum computing.
This is a repost from a post I wrote earlier this week.
Great post :)) check out my latest post as well :)
We need a huge quantum cell for algorithms.
What is the biggest now? 1000 quantum dots?
QP != NP (I think), so it is safe.