Predator-Prey Equations and the Steemit Ecosystem

The classic predator-prey equations were developed in the 1920s, but it was not till the 1960s that they started to be used in economics. The solutions to the equations describe what happens to two interacting populations, one preying on the other.

Without going into the mathematical solutions, a descriptive solution makes the interaction clear. As the predators feed themselves and increase their population, so the number of prey decreases. This results in less food being available for the predators so their population also then starts to decrease. With fewer predators around, the population of the prey starts to rise again (assuming it hasn't become extinct). As the number of prey increases, so the predators can feed again and their population starts to rise too. The cycle then continues.

Depending on the parameters in the equations, the rise and fall of the two populations will look something like the graph below.

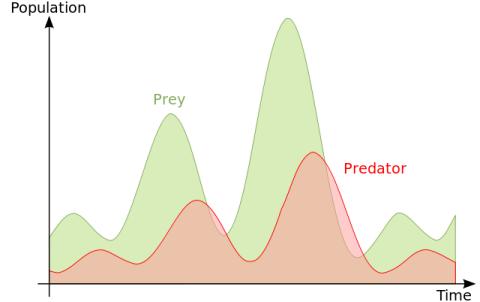
There are also a number of simulations you can play with to see what happens as you change the parameters, such as here andhere. As I said, this isn't about solving the equations, but I do want to show what they look like to explain certain qualitative features.

Here x is the prey and y is the predator. Notice firstly that there are two equations that share the variables x and y; this is a mathematical way of expressing the feedback mechanisms between the two populations. The equations are also completely deterministic; this means that starting with the same parameters and populations, the system will evolve in the same way. This is not the same as being predictable; the only way to see the future is to run the evolution of the equations in time. There is no short-cut algebraic way to determine what happens; this is just like generating fractals - and just like life itself.

So how is all this relevant to Steemit? If we move away from the original predator-prey metaphor and look at the same equations used in an economic context we see some interesting features. Let us replace predators and prey with "users" and "steem". The expression ax is a measure of how much "food" is available, in this case the amount of Steem available. However, the expression cxy tells us that the growth of the users is dependent on both its population and of how much Steem is consumed. If Steem is being consumed to such an extent that the buffer is close to depleted then the population of users can only feed on what is created daily. This may be too low for some users and the active population declines.

This is undoubtedly simplistic, but what I wanted to show is that the rules of the game have feedback loops within them, whether by design or by human interaction. The current set of rules is rather simple to manage all the different types of human interactions possible. But if the set of rules are to change they will be a mixture of positive and negative effects, just as in the predator-prey equations. But, (and here comes another important point) it is not possible to pick and choose the rules that you may prefer as they are in place to generate a particular dynamic. Tweaking such rules in an artifical system such as Steem should be the norm rather than the exception, until such time as the system appears to be dynamically stable.

For example, if we wanted to ignore one of the two predator-prey equations, what would happen? Well, depending on the values of the parameters and solving for just one equation, we will get either exponential decay or exponential growth - the system will either explode or implode. It is the feedback between the equations and well-chosen parameters that leads to a dynamical equilibrium.

---

You may also wish to read:
Ideas for Future Rule Changes - Voting, Earnings, Maximum Social Benefits - a Discussion Document