[금융선형대수] 기말 시험 전 정리(2)



※ 시험 전 정리용으로 작성자 외에는 알아보기 힘들 수 있음

편의 상, 벡터는 굵게 표시한다. 벡터 공간, Set, Matrix는 이탤릭체로 표시한다.

---

V를 벡터 공간이라고 하자

만약 V가 n개의 벡터들을 가진 basis를 가진다면, 우리는 V가 n-차원을 가지고 있다고 말할 수 있다

V의 subspace(부분공간) {0} 은 0차원을 가지고 있다고 말할 수 있다

V를 유한한 벡터들의 집합이 span할 때 V가 finite dimensional(유한차원)하다고 불린다

그렇지 않으면 infinite dimensional(무한차원)하다

---

Theorem 6

만약 V가 n > 0 차원의 벡터 공간일때, 모든 lienarly independent한 n개의 벡터들의 집합이 V를 span한다; V를 span하는 n개의 모든 벡터들은 linearly independent하다

---

Theorem 7

만약 V가 n > 0 차원의 벡터 공간일때, n개 보다 적은 벡터들은 V를 span할 수 없다

n개의 linearly independent한 벡터들보다 적은 수의 모든 subset은 V의 basis를 형성하기 위해 확장될 수 있다

n개의 벡터들보다 많은 수의 모든 spanning set은 V의 basis를 형성하기 위해 pared down될 수 있다

---

만약 A가 m × n 행렬일때, R^1×n의 부분공간이 row vectors에 의해 span될 때 그것을 A의 row space라고 한다

R^m×1의 부분공간이 column vectors에 의해 span될 때 그것을 A의 column space라고 한다

Theorem 8

두 개의 row-equivalent matrices는 같은 row space를 가진다

행렬 A의 rank는 rank(A)라고 쓸 수 있고, 이것은 A의 row space의 dimension이다

---

Theorem 9

linear system Ax = b가 consistent하다는 것의 필요충분조건은 b가 A의 column space안에 있어야 한다는 것이다

homogeneous system Ax = 0가 trivial(명백한) solution x = 0을 갖는다는 것의 필요충분조건은 A의 column vectors 들이 linearly independent하다는 것이다

---

Theorem 10

A가 m × n 행렬이라고 하자

linear system Ax = b가 모든 b ∈ R^m에 대해 consistent 하다는 것의 필요충분조건은 A의 column vectors가 R^m을 span한다는 것이다

system Ax = b가 모든 b ∈ R^m에 대해 대부분 하나의 solution을 갖는다는 것의 필요충분조건은 A의 column vectors가 linearly independent하다는 것이다

---

A가 m × n 행렬이라고 하자

만약 A의 column vectors가 R^m의 basis를 형성한다면 n = m이다

n × n 행렬인 A가 nonsingular하다는 것의 필요충분조건은 A의 column vectors가 Rⁿ에 대해 basis를 형성한다는 것이다

---

Theorem 11

The Rank-Nullity Theorem

만약 A가 m × n 행렬일때, the rank of A와 the nullity of A의 합은 n과 같다

만약 A가 m × n 행렬이고 U가 row echelon form of A일때, column vectors가 동일한 dependency relation을 만족한다

x₁a₁ + x₂a₂ + ... + x_na_n = 0

↕

x₁u₁ + x₂u₂ + ... + x_nu_n = 0

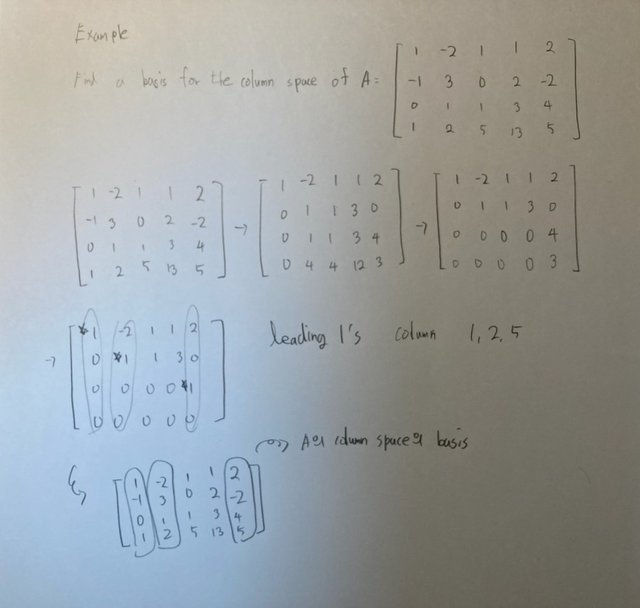
A의 row echelon form U를 통해 A의 column space의 basis를 찾을 수 있다

We need only determine the columns of U that correspond to the leading 1's. These same columns of A will be linearly independent and form a basis for the column space of A.

The row echelon form U tells us only which columns of A to use to form a basis. We cannot use the column vectors from U, since, in general, U and A have different column spaces.

아래는 A의 column space의 basis 찾는 과정