Steem Voting & Downvoting Game Theory

The following is not a complete analysis of all the possible strategies and counter-strategies that come into play when looking at the upsides and downsides of down-voting .

Assumptions:

• A linear rewards curve.
• For sake of simplicity there is no reverse auction for curation rewards.
• Three players A,B & C.
• C Either downvotes A&B or A or B or only selfvotes.
• A & B may cooperate (vote for each other or vote against C)
• All players have 1 vote worth 2 shares.
• When downvoting players (users) will try to bring the others to zero shares.
• The rows represent the strategies of A & B & the columns the ones for C.
• The payouts at the intersection of each strategy represent the percentage of the rewards that each player will get. The first payout is for player A, the 2nd is for B & the third is for C.

The case where B does not vote for A is a mirror image of the case where A does not vote for B, therefore it is omitted. The same goes for when B downvotes C.

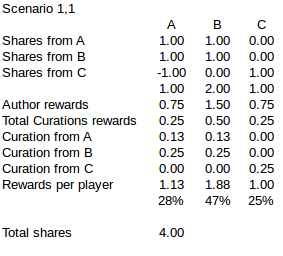
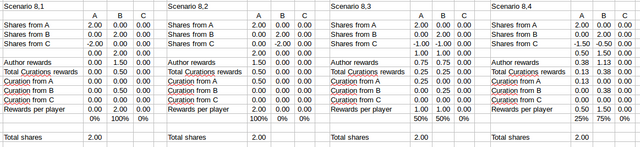
This is how scenario 1,1 (row 1, column 1) is calculated:

Suppose that C is a known spammer and A & B never upvote the posts from this user. In row 1 neither A or B downvote C. As you can see if C is trying to maximize the rewards it is not a good plan to downvote. Why? Because in order to downvote another player/user C will need to sacrifice voting power when self-voting.

Here are the rest of the calculations for row 1:

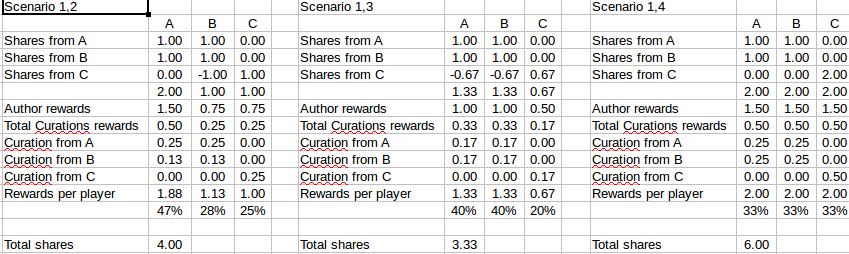
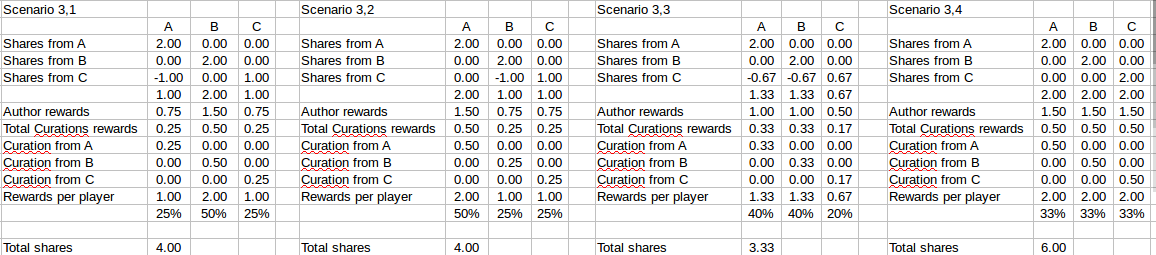
These are the ones for row 2 (please note that A does not vote for B but B does vote for A):

These are the ones for row 3:

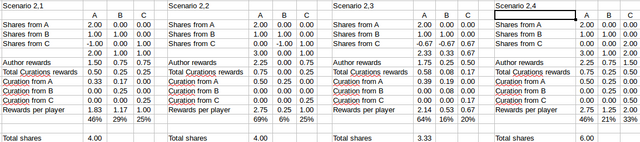
And here are the ones for row 4:

And finally row 5:

In scenarios (1,4); (2,4) and (3,4) there are no downvotes. Player C would maximize the rewards and there is nothing A or B can do to stop it.

However if A & B cooperate and both downvote C they can minimize the rewards for C (row 5).
If C downvotes both A & B then they can counter by cooperating.

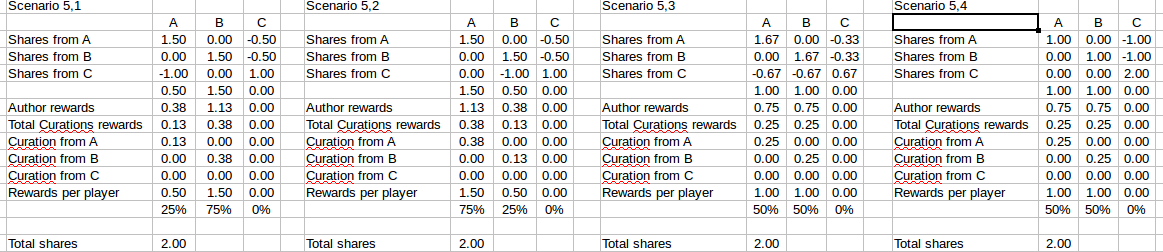
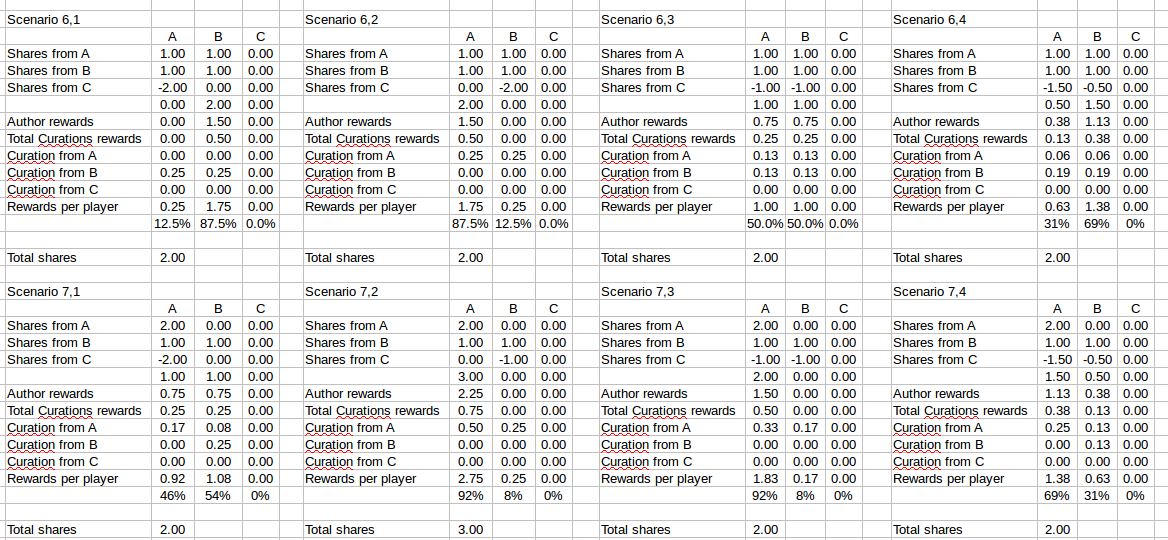
What happens when C only downvotes but does not post anything? (Bad actor or an external agent trying to screw with the platform).

In these situations the best outcome would come from:
(6,3); (7,1) & (8,3)

The first 2 involve cooperation:
(6,3) A & B help each other
(7,1) B helps A

In (8,3) C just dilutes it's downvotes with a net effect of zero.

These are the calculations:

These is an over-simplified model that doesn't consider the cases where the voting power is not equal. If I have time I will attempt to make a model for some of those scenarios.