Understanding p-values for dummies and doctors: Flipping a potentially biased coin.

Normally the subjects I blog about have to do with nutrition, lifestyle, and health. I often talk about the data science and engineering aspects of these subjects, but normally always in the context of these base subjects. In my last blog post I talked about using epi data sets to determine when claims from supposedly better sources of evidence should be ignored anyway. I talked about the use of a claimed effect + effect size as the null hypothesis, and of cause touched on p-values. While p-values are no rocket science, some recent discussions on twitter showed me just how misunderstood this relatively simple subject seems to be. Many people, often people with a solid background in medical or nutritional science as well, seem to have weird ideas about p-values and their implications. There is much to find on the internet on p-values, but especially for people who don’t use mathematics in their daily work, most of these explanations can seem like magic incantations and don’t truly help in providing a quick basic grasp of the subject.

For this reason, I now make this sidestep from my usual blogging subjects and do a post on probability and p values. In this post, I want to try and give a simple example of what p-values tell us and more importantly what they don’t tell us. To do this, we are going to take a large step back from nutritional and medical studies, back to the number one school example of trivial probability concepts, the flipping of a coin. We won’t go into any of the potentially confusing stuff about probability distributions and statistical tests, just the very most basics of probability reasoning needed to understand some of the basic implications of p-values, using nothing but a bunch of coin flips.

A simple Markov model

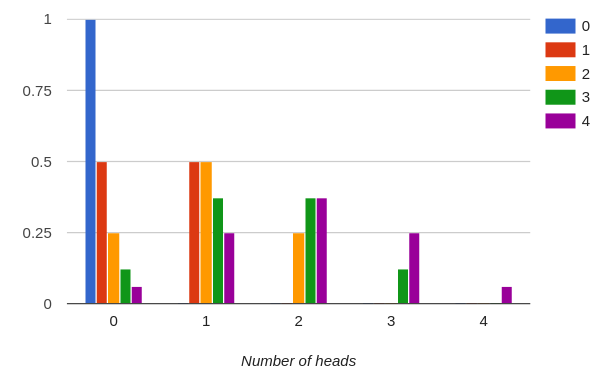
As you will know, if you flip an unbiased coin, the probability of it landing on heads will be 50% or 0.5, as will the probability of it landing on tails. If you flip the same coin twice and count the number of times the coin lands on heads, the probability of zero heads will be 0,25, the probability of one head will be 0,5 and the probability of two heads will be 0.25%. With two throws, there are four possible sequences of flip outcomes. Heads heads, heads tails, tails heads and tails tails. Each sequence has a 25% chance of ocurring, but as borh heads tails and tails heads add up to a single heads, the one heads outcome has a 50% probability. If we increase the number of throws, to let’s say four throws, a kind of a hump-shaped histogram starts to form.

One useful way to look at out coin flip, and a good way to determine the probabilities of different head counts occurring, is to view each possible number of heads thrown so far as a state in a state machine. Before we start our four throws, the probability of the zero heads state will be 100%. For each throw where the state is ‘zero heads’, the probability of traversing to ‘one head’ state at the next throw will be 0.5 and the probability of remaining in ‘zero heads’ state after the next flip will be 0.5.

The same is true for all other states in our state machine. The probability of remaining in state N is 0.5 and the probability of moving on to state N+1 is 0.5. When you actually flip the coin, you will always know what state you are in after the coin flip. If however, we refrain from actually flipping, we can assign probabilities to each of the possible states, and in doing so turn our state machine into a simple Markov model.

So after one flip, p(S0), the probability of having thrown a total of zero heads, will be 0.5; p(S1), the probability of having thrown a toatal of one heads, will be 0.5 as well. Now when we throw again, the probability of ending up in S0 will be 0.5 times the probability that we were in the S0 state, to begin with. The probability of ending up in S2 would be 0.5 times the probability that we were in S1 to begin with. And finally, the probability of ending up in S1 would be 0.5 times the probability we started out in S0 plus 0.5 times the probability we started out in S1.

The above diagram shows what happens to our Markov model when we flip our unbiased coin four times. It might be useful to look at the same data as histograms:

Let us look at the histogram for four flips, and let us say our four flip experiment is meant to be a test for biased coins. Given the 50% probability of throwing head on a single flip of an unbiased coin, if we repeated our four throws experiment a thousand times, the average number of heads in four throws should be something very close to two. Two is our expected value. Now it is time to look at the concept of p-values. The p-value for our result is the probability given zero non-random effects, a deviation from the mean at least as big as the one observed would be observed. If we throw two heads, the deviation from the mean is zero and our p-value will be 1.0. If we throw one or three heads, the deviation from the mean is one, and the p-value will be the sum of the probabilities of throwing zero, one, three and four heads, or 0.625. If we throw zero or four heads, the deviation from the expected value will be two, so the p-value would be the sum of the probabilities of throwing zero or four heads: 0.125, or 12.5%.

Note that p values only have meaning if we have what is called a NULL hypothesis. In the example we have been using here, the null hypothesis has been: “our coin is an unbiased coin”. We shall later see that the use of a different NULL hypothesis could sometimes yield useful results.

Statistical significance

So now we come to statistical significance. The basic idea behind p-values is that they are our first line of defense against spurious nonsense. It should never be our only line of defense though, and that should be something to remember. As we have seen in our four flip experiment, the lowest p-value achievable was 0.125. There is a commonly used. yet arbitrary threshold for p values that denotes ‘statistical significance’ and that threshold value is 0.05. Anything below that threshold is called statistically significant. Now so far everything is fine and dandy, but there are two caveats with this threshold. Let’s say I am an incompetent minter and due to some unfortunate incident, I have produced ten million two euro coins that have the same image on both sides of the coin. Half the coins have two heads and the other half have two tails. You would be so happy with the four flip test, as it would never be able to show a statistically significant test outcome, and given that half the coins would be double head and the other half would be double tail, a meta-analysis of multiple tests should show the expected mean of two heads or something pretty close. We can say that the four flip test is under-powered. No matter how strong the effect, a four flip test could never lead to statistical significance and thus could never lead to any evidence against the null hypothesis. This, however, can easily be fixed by adding more coin flips for the same coin. If for example, we increase the number of flips from four to twenty, the p-value for an unbiased coin ending up on the same side for twenty consecutive times would be less than 0.000002. Now this effect is of course extreme. Let us look at a bit less extreme example now. Let’s say a coin was discovered that is biased to such an extent that a flip will end up on head 75% of the flips. Still a very strong effect, but one that can help us illustrate some of the less appreciated subtleties of probabilities. Remember the p-value tells us something about the probability of an outcome given that the null hypothesis is valid. It does NOT tell us anything about the probability that the null hypothesis is valid given the outcome. To understand this, we need to look at the probabilities of totaling N heads in 20 flips for both the unbiased as the severely biased coin.

The probability of the outcome given the null VS probability of validity of the null given the outcome

Now let us look at a twenty flip test. Consider we flip a coin twenty times and the number of times the coin lands on heads 15 times. Let us assume the (in reality normally quite rare) situation that we are 100% sure of the direction of the effect. That is, we know for sure that only biased coins may exist that favor head, in this case, we have knowledge about the properties of the biased coins that are in circulation. Given these exceptional circumstances, we opt for a one-tailed approach to the problem, so instead of looking at the deviation from the expected value, we look at the probability that the number of heads is at least 15. So what p value do we get here if the null hypothesis is that our coin is unbiased? The p-value for our outcome of 15 heads out of 20 flips is 0.021. We have statistical significance. But does this mean we have found a biased coin? The number of heads is exactly the expected value for a biased coin, so it would seem we have successfully identified a biased coin here, right? Well no. Or at least, it depends. The probability of this exact outcome for an unbiased coin would be 0.015 or 1.5%. The probability of this exact outcome for our severely biased coin would be 0.2 or 20%. If 50% of all coins were biased, the probability of the coin in our test is a biased coin would be 0.93; 93% giving us a 7% false positive rate. Notice this is already a probability a number of times higher than the p value? These probabilities are very much different things. But then, 7% false positives still sounds pretty much acceptable, right? Look what happens if only one in a thousand coins would be a biased coin. The probability that the coin in our test is indeed a biased coin if one in a thousand coins is biased would end up at about 0.014 or 1.4%, or to say it differently, we would end up with a false positive rate of 98.6% if we used significance as proof that a coin is biased.

Regression to the mean

Now let’s consider we are looking at a possible solution for ‘fixing’ biased coins, what could go wrong? In our example, we know how many unbiased coins there are for each biased coin, and we know exactly what the probabilistic properties are of both coin types. Normally, however, this knowledge would be obscured from view. One thing we do know however is that if we divide our population of coins into a sub-population of coins who test at 0..14 heads and a sub-population of coins who test at 15..20 heads, then the probability of ‘being a biased coin’ is quite a bit higher for the 15..20 heads group. Or as it is referred to in medical studies, the 15..20 heads group have an increased RISK of being biased coins. So what about fixing our biased coin problem based on the risk reduction paradigm? How would we go about that? One way to approach this, a way not uncommon in medical science literature is doing a Randomized Controlled Trial (RCT) using only the high-risk group. Such a trial could be designed as follows:

We take 100,000 coins and flip each of these coins 20 times.
Those coins for what the 20 flips result in less than 15 heads are discarded.
The remaining coins are divided up into two equally sized groups of coins.
The first group of coins is sprayed on the head side with a substance meant to give slightly more weight to the heads side of the coin.
The second group of coins (the placebo group) is sprayed only with pressurized air (the placebo).
The coins in both groups are flipped 20 times a second time and the results for the two groups are compared
Let pick some real numbers for our RCT and see what happens:

One in a hundred coins is biased in the way described earlier (75% probability of heads)
A biased coin that is treated has its bias reduced but still remains biased (70% probability of heads)
An unbiased coin that is treated has its bias increased, but in the other direction (45% probability of heads)
So let’s look at the first two steps, we have 100,000 coins, 99,000 unbiased coins and 1,000 biased coins that are flipped 20 times each.

2,049 unbiased coins out of the 99,000 end up as false positive.
585 biased coins out of the 1,000 end up being correctly identified
Our trail starts off with 2634 ‘high risk’ coins.
The remaining 97,366 coins are excluded from our trail.
The average head count is 15.5
Looking at these figures we see that as a risk marker, the test outcome is pretty good. The risk of being a biased coin is more than 22 times as high in the identified high-risk group as it is in the general population of coins. We are not talking about marginal 10% or 50% risk increase. Our risk increase is a whopping 2100%, so that sets some expectations, right? But lets not get ahead of ourselves. We have some more steps to conclude.

So on to the next step. The coins are divided into two groups of 1317 coins:

The treatment group consists of 297 biased coins and 1020 unbiased coins
The placebo group consists of 288 biased coins and 1029 unbiased coins.
The average head count in both groups is 15.5
Now let’s first look at the results:

The average head count in the treatment group went down from 15.5 to 10.13
The average head count in our placebo group went down from 15.5 to 11.1
So what is this? Are our coins affected by a placebo effect? Well, no of course! What we are seeing here is a very simple example of the probabilistic phenomenon known as regression to the mean. A full explanation of this concept falls outside of the scope of this post, but the part that is most important to realize that the process of selecting only one tail of a distribution for use in an RCT is a sure way to introduce an effect that medical papers all too often misclassify as a placebo effect, or as it’s mirror image, a nocebo effect. One thing to realize is that you can’t fix or adjust for regression to mean, you need to protect against it in your trail design. As a rule of thumb, I pose that it is fair to say that unless a paper that claims a placebo or nocebo effect explicitly mentions RTM protection, you may assume the effect to be attributable to regression to the mean effects. A medical science paper showing results like the ones we just demonstrated may claim a sizeable placebo effect, but may also claim a reduction of the number of biased coins is provided by the treatment. When we zoom into what actually happened to our treatment group we note that we started out with 297 biased coins, and after treatment ended up with 1317 biased coins. An actual increase in the number of biased coins of over 340%. Given that our goal was to reduce the number of biased coins, it would be fair to say that the RCT results are very much misleading.

One-tailed vs two-tailed tests

With our biased coins, we have been using a one-tailed test. This was kind of justified for the reason that we were 100% certain that bias would express itself in only one direction. Now that we have started with a ‘treatment’ for biased coins, however, this prerequisite no longer holds. If somehow we would become misled into believing our treatment should be extended to treat an even wider range of coins, our population of coins could end up with a very large sub-population of coins biased towards landing tails up. In that case, our one-tailed test would structurally be testing the wrong tail for any of these coins. In a one-tailed test, a strong effect towards the opposite tail that in a two-tailed test would be significant will end up with a p value falsely suggesting complete randomness. But this is by far the only issue. As we know, significance is denoted by an arbitrary threshold value of 0.05. Given that this 0.05 probability in a two-tailed test will be divided over the two tails, while in a one-tailed test, the 0.05 will all be in the one tail we expect the effect to be. This fact opens up a loophole for fraudulent significance. That is, an outcome with just short of denoting significance could be made believed to be a statistically significant outcome. Summarizing, one-tailed tests make significant outcomes opposite from expected outcomes seem insignificant while making expected outcomes seem (more) significant than they actually are. As such, it is rarely justified to use one-tailed tests. I’m hesitant to call one-tailed tests inherently fraudulent, but their usage should definetely be viewed with suspicion.

Swapping the null

Now let’s say we examined a coin three times in a twenty flip test, Two tests yielded a response with a sufficient strength in the expected direction to denote significance. A third test, however, gave us a result in the other direction. A result, however, lacking statistical significance. The naive approach to these outcomes would be to say the non-significant result should be ignored as it lacks significance, while the statistically significant results should not, and thus together strengthen the level of evidence we have for the fact that the coin is a biased one. Now let’s examine it a bit closer. If for example the first two outcomes yielded fifteen heads each, but the third yielded only seven, the seven, at a p-value of 0.07 won’t denote significance against the null that assumes a non-biased coin. But now look what happens if, prompted by the first two results, we decide to swap the null and assume the coin to be biased. The p-value for the last test would end up at a very much significant value of 0.00024. In contrast, the other two tests yielded a p-value of 0.01 against the original null, or if we combine the two, a combined value of 0.0001 combined. Notice how our previously insignificance is giving our two significant finding a good run for its money?

Take home points

So what are the important lessons to take from this simplified discussion of p-values?

Always consider if a study actually COULD show statistical significance (four flip example).
If it could and it doesn’t, consider the fact that there is no significance, significant (pun intended).
Statistical significance or a low p-value on its own does not say as much about the probability of the null hypothesis given the outcome. (one in a thousand biased coin example)
Be wary of studies showing a placebo or nocebo effect (regression to mean)
Be wary about the use of one-tailed tests.
Don’t let converging evidence go unchallenged; swap the null and look at the non-sig outcomes once more.
P-values are no rocket science. They are simple probabilities, yet they seem the source of a lot of confusion, even to many educated smart people. I hope that this post, while not mirroring the typical trail context provides sufficient insights into the misinterpretations we should take care to avoid.