이원 분산분석 (two way ANOVA) 숙제 - R 코딩
# 이원 분산분석에 대한 과제가 있어, 그것에 대한 풀이 과정입니다. 답이 맞는지는 모르겠네요. 이원 분산분석에 대해 명쾌하게 설명이 된 글을 찾기가 쉽지는 않아서 시간이 좀 많이 걸렸어요.
(문제)
※ R 프로그램에 기본으로 포함된 mtcars 데이터를 이용하여 다음 질문에 답하시오.
(모든 가설검정 문제에 대해 유의수준 0.05를 이용할 것)
[데이터 설명] mtcars 데이터는 1974 년 미국 Motor Trend Magazine 에 발표된 데이터로서 32 개의 차종에 대해 단위 연료 당 주행 거리(miles/gallon) 및 일부 특성을 조사한 데이터이다.
우선 다음의 R script 를 실행하여 mtcars 데이터의 변속기 종류(am)와 실린더 개수(cyl) 변수를 factor 형태로 변환한다.
mtcars$am <- factor(mtcars$am, levels=c(0, 1), labels=c("Automatic", "Manual"))
mtcars$cyl <- factor(mtcars$cyl, levels=c(4, 6, 8), labels=c("4cyl", "6cyl", "8cyl"))
- 변속기 종류(am) 및 실린더 개수(cyl)에 따라 주행 거리(mpg)의 평균에 유의적인 차이가 존재하는지 확인하고자 한다. 변속기 종류(am) 및 실린더 개수(cyl)에 따라 주행 거리(mpg)의 평균에 유의적인 차이가 존재하는지 이원 분산분석(Two-way ANOVA)을 수행하고, 그 결과를 간단히 해석하시오.
(단, 교호작용(interaction)을 포함할 것이지 여부는 스스로 결정할 것)
그리고 이를 이용하여 어떤 경우에 주행 거리(mpg)의 평균이 가장 높은지 간단히 설명하시오.
--
(풀이) - R 코딩
summary(mtcars)
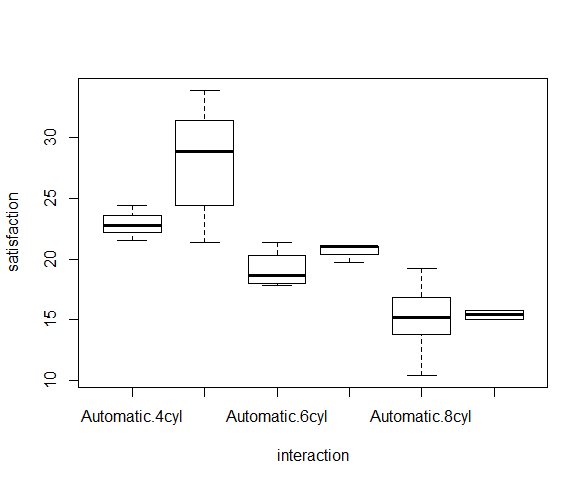
boxplot(mpg ~ am*cyl, mtcars, xlab="interaction", ylab="satisfaction")
with(mtcars, interaction.plot(am, cyl, mpg))
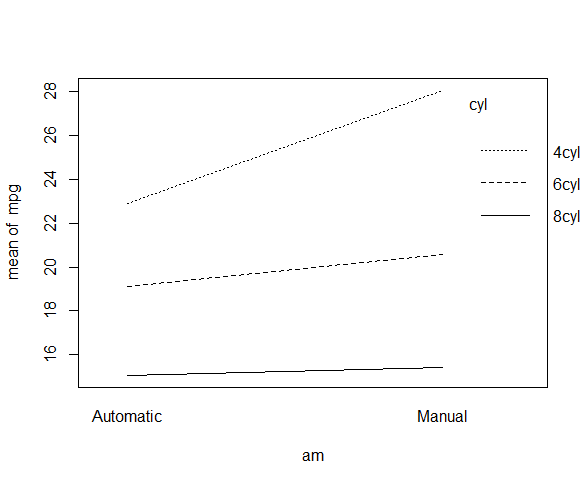
# 그래프가 교차하지 않아 교호작용이 없다고 볼 수 있다.
mtcars.aov2 <-aov(mpg ~ am * cyl, mtcars)
summary(mtcars.aov2)
# am:cy1에서의 p-value 0.269로 0.05보다 크므로 그래프에서와 동일하게
# 교호작용이 없다고 볼 수 있다.
# 그리고, 변속기 종류와 실린더 개수는 p-value가 0.05보다 크므로
# 둘 다 평균의 차이가 있다고 볼 수 있다.
model.tables(mtcars.aov2, type="means")
# 변속기가 수동이면서 실런더가 4개 일 경우( Automatic - 4cyl ) 가
# 주행거리 평균이 가장 높다.
mtcars.am.ph <-TukeyHSD(mtcars.aov2, which="am")
mtcars.am.ph
plot(mtcars.am.ph)
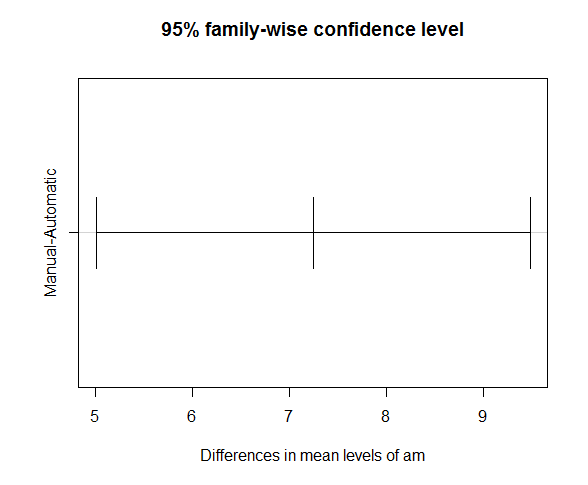
# 변속기가 수동과 자동은 유의한 차이가 있다고 볼 수 있다.
mtcars.cyl.ph <-TukeyHSD(mtcars.aov2, which="cyl")
mtcars.cyl.ph
plot(mtcars.cyl.ph)
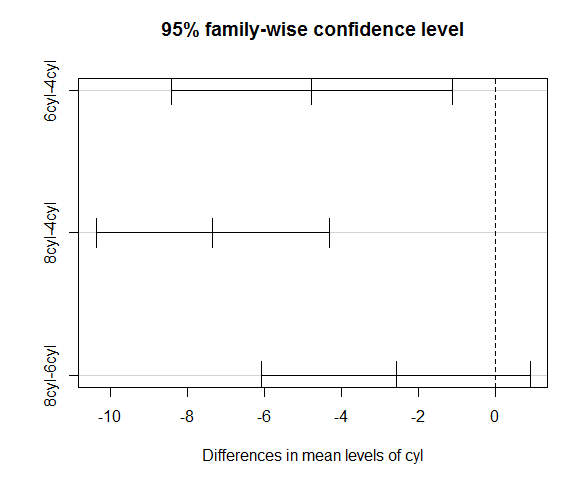
# 실린더가 6개와 8개는 유의한 차이가 없고 나머지는 유의한 차이가 있다고 볼 수 있다.