El interés compuesto y la función exponencial
En el post de hoy, mostraré como se deduce la muy conocida fórmula del interés compuesto y como está relacionada con la función exponencial.
La función exponencial se basa en la constante matemática e ≈ 2.7182… El matemático suizo Jacob Bernoulli, se “topó” con esta constante en el año de 1680, cuando estaba estudiando precisamente el interés compuesto.
La fórmula para el capital acumulado luego de n años de reinvertir un capital inicial x0, con una tasa de interés anual fija i, y con una tasa de reinversión de k veces al año es:
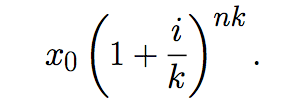
A continuación se ilustrará como deducir esta fórmula.
Supóngase que se tiene un capital inicial de x0 y que este se invierte a una tasa fija de interés i, por un año (se puede usar otro lapso de tiempo, pero para fijar ideas se supondrá que el periodo de tiempo es un año). Al finalizar el lapso de un año el capital acumulado es x1, donde x1=x0(1+i). Ahora si se reinvierte el capital x1 bajo las mismas condiciones, luego de un año más, el capital acumulado es
x2=x1(1+i)=x0(1+i)2.
Así luego de n años reinvirtiendo los intereses generados, el total capital acumulado es
xn=xn-1(1+i)= ... =x0(1+i)n.
Si se modifica la estrategia de inversión. Suponga que los intereses son pagado cada seis meses, al cabo de seis meses el capital es
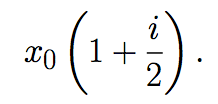
Ahora al depositar este capital bajo las mismas condiciones, el capital acumulado en los próximos seis meses es
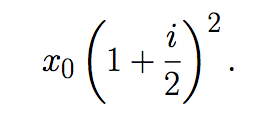
Si se mantiene esta estrategia por n años el capital acumulado, viene dado por la expresión
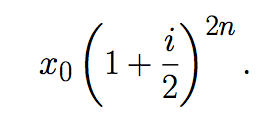
Suponga ahora que los intereses son pagados cada meses y estos recapitalizados, al finalizar el año el capital acumulado es de
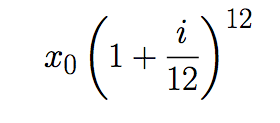
y luego de n años el capital será
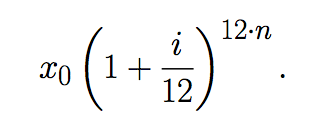
Si los interesa son pagados diariamente y recapitalizados, el capital acumulado luego de n años (suponiendo que todos los años tienen 365 días), es
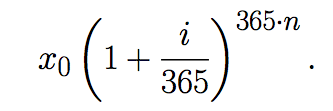
¿Qué ocurre si los intereses son pagados cada segundo y estos capitalizados inmediatamente? ¿O si esta operación se realiza de manera continua? La respuesta es el resultado del límite
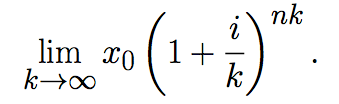
Resulta ser que ser este es un límite bien conocido:
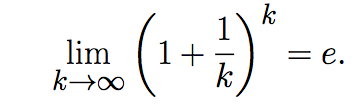
Jacob Bernoulli lo trabajó en 1680.
De esta expresión se deduce inmediatamente
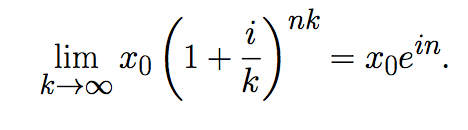
Por lo tanto el capital acumulado luego de n años es xn=x0ein.
De aquí se puede observar que la última expresión es la solución de la ecuación diferencial x(t)´=ix(t). La cual plantea que la tasa de cambio (crecimiento o decrecimiento ) del capital es directamente proporcional al capital existente y la constante de proporcionalidad, viene dada por la tasa de interés.
Ahora uno se puede preguntar en cuanto tiempo se tarda en duplicar la inversión original, asumiendo una recapitalización continua. Para ello se requiere xn=2x0, por lo que sigue
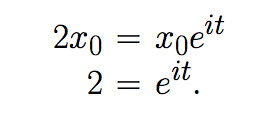
Por lo tanto el tiempo para duplicar la inversión es
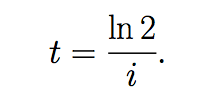
Referencias:
https://en.wikipedia.org/wiki/Compound_interest
https://en.wikipedia.org/wiki/E_(mathematical_constant)
Es una lástima que no haya visto este post antes para votarlo. Me encanta la matemática. Te sigo
Regularmente publico temas sobre matemáticas en mi blog. Gracias por su interés.
Muy buena explicacion! Detallada y facil de entender. Excelente post!
Gracias por su comentario. Observo que usa como imagen el retrato de Gauss.
Muy buen post, ayudo mucho a mi hermano que andaba buscando esta información.
Que bueno que el post haya sido de utilidad para su hermano.
Great Job NYC post Follow Me Steemit Get More Upvotes And Upvote My Articals @wajidali
Hola mis mas cordiales saludos @nenio ultimamente he observado sus publicaciones, en especial las de carácter científico como esta!, le escribo primero: para felicitarlo por el post y en segundo lugar quiero hablar con usted y contarle sobre un proyecto que la comunidad steemSTEM quiere iniciar.
Si gusta puede entrar al enlace del canal y contactarme en privado muchas gracias de antemano, espero su pronta respuesta.