La Helena de los geómetras.
La cicloide.
Una curva con bellas propiedades que creo disputas entre los matemáticos del siglo XVII por lo cual se ganó el apodo de "la Helena de los geómetras", fue estudiada ampliamente a lo largo de la historia y es la trayectoria que sigue un punto de la circunferencia al girar sin resbalar sobre una recta. Sobre quién fue el descubridor de esta curva hay varias hipótesis pero fue el grandioso Galileo Galilei quien acuñó el término y el primero en hacer un estudio riguroso sobre ella.
Dependiendo de dónde esté ubicado el punto respecto a la circunferencia tenemos tres tipos de cicloide: común, alargada y acortada.
La curva azul generada por el punto C’ sobre la circunferencia es una cicloide común, la amarilla generada por el punto D’ que esta fuera de la circunferencia es una cicloide alargada y la curva roja, generada por el punto B’ dentro de la circunferencia es una cicloide acortada.
Mismo Tiempo.
Si teniendo tres rampas idénticas y en cada una de ellas una bolita idéntica a la otra pero colocada a una altura distinta sobre la rampa y les pregunto ¿Cual bolita llegará primero al final de la rampa? De seguro me dirán que la que esté más cerca del final pero, ¿Que pensarían si les digo que hay una curva con la cual indiferentemente de la posición en la cual se encuentren las bolitas todas llegaran al final al mismo tiempo? Esto no parece muy cierto pero es así y esta curva es la mismísima Cicloide.
La cicloide es una curva con propiedad tautócrana, esta palabra significa mismo tiempo del griego -tauto- que es "mismo" y - chrono - "tiempo". Huygens en 1659 demostró que la tautócrana era una cicloide, publicandolo en su Horologium Oscillatorium.
En un cicloide cuyo eje se eleva sobre la perpendicular y cuyo vértice está localizado en el fondo, el tiempo de descenso en el cual un cuerpo llega al punto más bajo, al vértice, después de haber partido desde cualquier punto del cicloide, es igual a cualquier otro.
Christian Huygens.
En otras palabras significa que en una cicloide invertida, un punto que desliza sin fricción en gravedad uniforme le toma el mismo tiempo llegar a la parte más baja sin importar a que altura se encuentre el punto de partida.
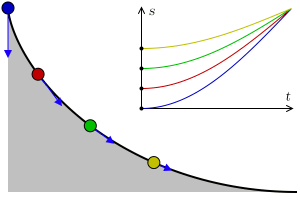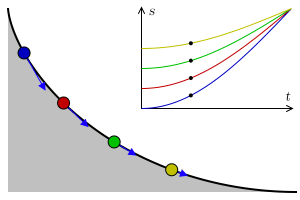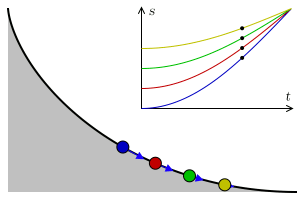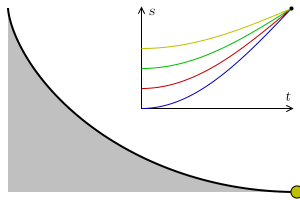
El más corto intervalo de tiempo
Ahora si les pregunto ¿cuál es la forma que debe tener una curva para que el tiempo del recorrido de un objeto que se mueve de A hasta B sea el menor posible? Seguramente pensaran que una línea recta por ser la distancia más corta entre dos puntos, pero no es así, esta curva es una cicloide.
La braquistocrona como se le conoce a la curva que cumple está propiedad es una cicloide invertida, este problema fue resuelto por Bernoulli en 1669 haciendo uso del cálculo variacional.
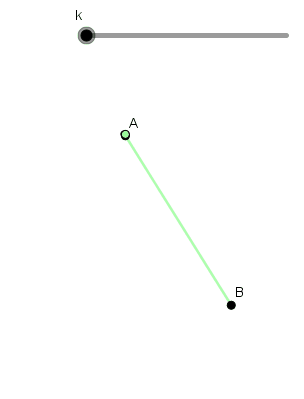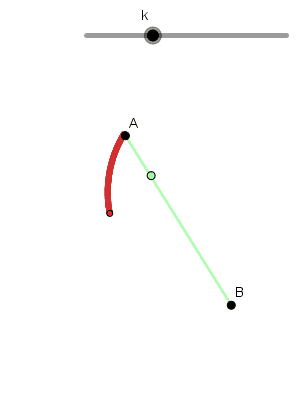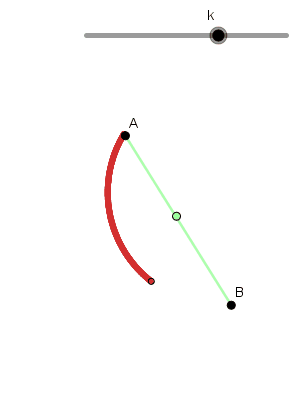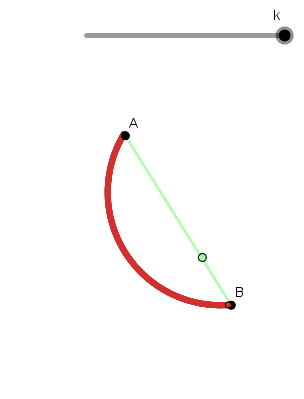
Para demostrarlo tomaremos un sistema de referencia cuyo origen se encuentre en "A", asi A = (x1,y1) = (0,0) y B = (x2,y2) = (d,-h). Debemos encontrar la expresión que nos permita calcular el tiempo, al ser el campo gravitacional conservativo la energía mecánica total de la particula se conserva.
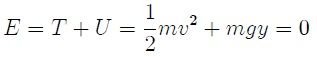
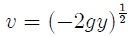
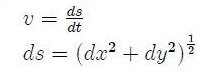
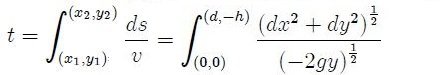
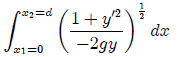donde el integrando es nuestro funcional.
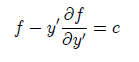
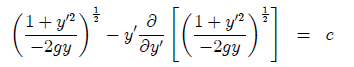
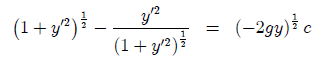
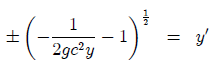
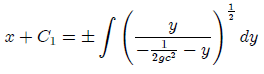(1)
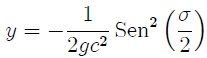
El signo negativo se debe al sistema de referencia usado.
Entonces se puede escribir como:
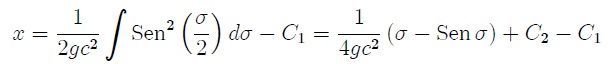
Donde C = C2 - C1
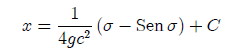(2) De (1) se obtiene que σ = 0 y de (2) C = 0. Entonces se pueden escribir como:
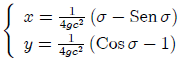
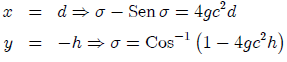
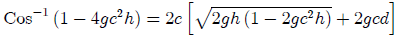
Completando así nuestra Cicloide que va de A hasta B.
Y así concluye este post, espero se hayan fascinado por la Cicloide y este par de interesantes propiedades tanto como lo hice yo y lo hicieron a lo largo de la historia grandes pensadores.
Referencias:
T. Soldovieri, (2017), Introducción a la mecánica clásica, Venezuela, 1era edición, P.P. 455-457.
Excelente libro creado por mi profesor de mecánica clásica.