¡Qué apasionantes son las matemáticas! muchas veces lo veo como un mundo mágico en el que todo tipo de ejercicios entran y nos ofrecen respuestas muy maravillosas. Desde pequeño siempre me han gustado, hoy quiero recordar un episodio que tuve cuando estaba en bachillerato: El cálculo de PI.

Cuando estaba en el colegio siempre estuve obsecionado con el valor de PI, siempre se nos decía que comenzaba por 3.14 y poco más... ¿y cómo saben que ese es su valor? me preguntaba yo, lo único que sabía era que correspondía a la razón entre la circunferencia y el diámetro. Recuerdo que una vez le pregunté a mi profesor de matemáticas por ello y él me contestó precisamente eso: "Coge una cuerda, la enrollas alrededor de un balde circular, marcas una vuelta y la mides; luego mides el diámetro; y finalmente divides los dos valores". Pero este método no me convencía mucho... las matemáticas son muy exactas como para tener que depender de un mundo real donde la exactitud está muy lejos.

Así que de tanto pensar un día se me ocurrió una idea. Los polígonos regulares (tríangulo, cuadrado, pentágono, hexágono, etc) mientras más lados tengan más se acercan a lo que es un círculo, ¿por qué no intentar unir estos 2 mundos? por ejemplo en su área y tratar de igualarlo para un polígono de infinitos lados.

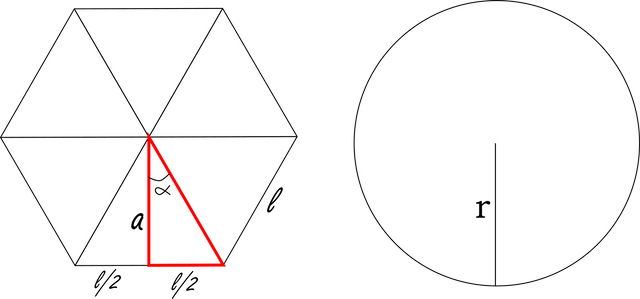
Si nos fijamos en la figura, un polígono regular lo podemos fragmentar en varios triángulos idénticos que apuntan hacia su centro, cuya base corresponde al lado del polígono, y la altura su distancia al centro. De la figura vemos que al fragmentar todo por el número de lados (n) el ángulo alfa es:

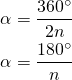
Luego, tomando el triángulo rectángulo podemos calcular su tangente y operar:

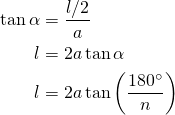
Luego el área será la suma del área de todos estos triángulos:

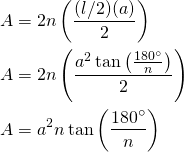
Bien, ya tenemos el área del polígono en función del número de lados, ya estamos cerca, ahora solo falta igualarlo con el área del círculo a ver qué sucede:

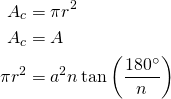
como en un polígono de infinitos lados todo se asemeja a un círculo, entonces la distancia a será exactamente el mismo r, por tanto:

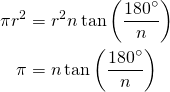
Con esto había logrado cancelar r!! wow que maravilloso, para mí esto fue como magia, un eureka por haber logrado separar PI de las áreas y las distancias y por fin tenerlo tan cerca, donde solo dependía de n que era infinito. Ahora solo me faltaba terminar de calcularlo. Ya para ese tiempo nos habían enseñado los límites así que continué rápidamente sin saber la sorpresa que me iba a llevar.

Por no entrar en muchos detalles, cuando un ángulo es muy pequeño cercano a cero, la tangente y el seno tienen el mismo valor. Por otro lado, en los límites debemos trabajar en radianes en vez de grados (180º=pi radianes), por tanto:

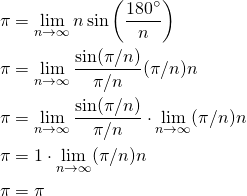
PI = PI !!!... bravo, aplausos... no jodás, ¿pi es igual a pi? ¿tanto trabajo para esto? Toda esa euforia que tenía y ese sentimiento de que había encontrado algo importante de un momento a otro se me esfumó entre las manos. No logré ver siquiera un 3.1, NADA!. En ese momento me desanimé por el resultado y esta idea quedó guardada por un tiempo en el cajón.

Con el tiempo comprendería que PI es una constante muy especial como para que se dejara encontrar tan fácil, que no se trata de despejar una simple ecuación.

Mi gran ayuda: El coseno del ángulo medio

Uno de los grandes problemas de esta fórmula de PI es que debemos calcular el seno de 180/n, y si n es infinito, quiere decir que debemos calcular el seno de un ángulo muy cercano a cero.

Con el tiempo se me ocurrió una idea: Una de las identidades trigonométricas es el seno y el coseno del ángulo medio. Entonces podría comenzar tomando el seno de un ángulo grande, como 90º, y después hacer cálculos sucesivos del ángulo medio hasta alcanzar un ángulo muy pequeño. Es decir, calcular el sin(90), luego el de sin(90/2), luego sin(90/4), luego sin(90/8), y así sucesivamente.

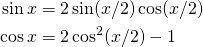
La identidad trigonométrica se vuelve más sencilla si trabajamos con el coseno, así que trabajamos con esta y despejamos:

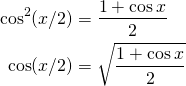
Y operando un poco más obtenemos la siguiente fórmula que nos será de gran ayuda:

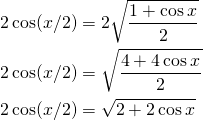
Aquí es donde viene lo interesante, comencemos con el coseno de 90º, y luego usando la fórmula anterior vamos calculando el coseno del ángulo dividido entre 2 de forma sucesiva:

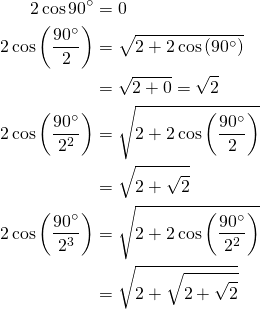
Si nos fijamos, cada vez que partimos el ángulo por la mitad, hacemos que su coseno tenga otra raíz de 2 anidada, qué interesante. Por ejemplo, cuando el coseno que tiene un 2 elevado a 3 tendrá 3 veces la raíz cuadrada de 2. Así que lo podríamos escribir de esta forma:

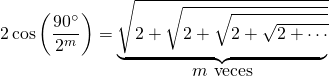
Una vez tenemos esto calculado, podemos aplicarlo a nuestra ecuación de PI. Para ello primero lo dejamos todo en términos del coseno:

Si tomamos a n como potencias de 2 podemos aplicarlo a la ecuación del coseno. Entonces digamos que 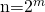, de esta forma tenemos el siguiente resultado:

Y una vez apliquemos nuestra fórmula del coseno obtenemos finalmente nuestra querida aproximación de PI:

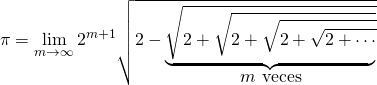
Wow!! que resultado. Cuando por fin lo encontré me emocioné mucho.

Y como dije más arriba PI es una constante muy particular como para que sea fácil expresar su resultado. Cabe destacar que existen muchas otras formas de aproximar a PI e inclusive unas mucho más fáciles de calcular que raíces cuadradas anidadas como es este caso. Sin embargo, aunque no es de lo mejor, quedé muy satisfecho con este resultado. Es una motivación más para seguir haciendo más cosas y enfrentar más ejercicios.

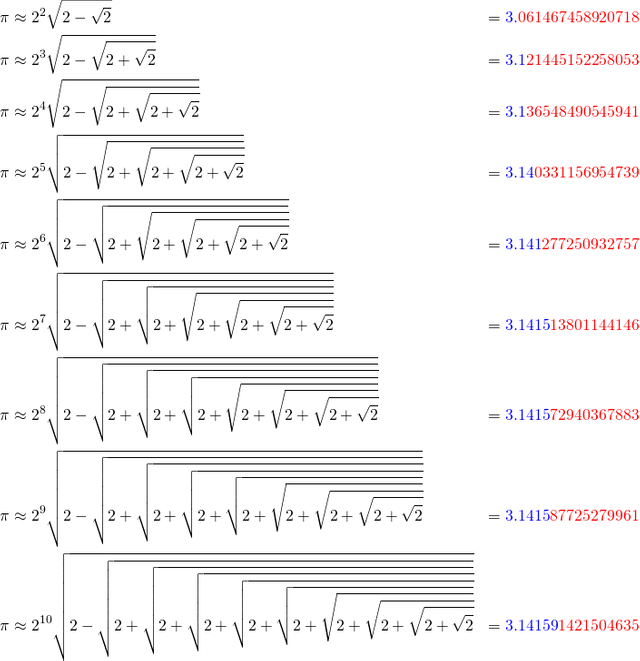
Por último, quisiera mostrarles qué tanto se aproxima su valor dependiendo del valor de m. Con letras azules marco los decimales que coinciden bien con PI, y en rojo los decimales que no coinciden.

¿Qué les parece esta aproximación? Espero que haya sido de agrado de todos. Mas allá de las fórmulas, el mensaje que quiero dejar es que siempre encontraremos dificultades en el camino, pero lo importante es tener paciencia y perseverancia, los cuales son nuestros aliados para alcanzar nuestros objetivos.