El lenguaje como una relación matemática
A simple vista, parece que las matemáticas y los lenguajes naturales no tienen mucho que ver, pero, de la misma forma que las matemáticas pueden explicarse en términos de un lenguaje natural, el lenguaje natural puede explicarse en términos del lenguaje matemático. Esto es lo que voy a demostrar ahora mismo.
En términos no muy formales, una relación matemática es una correspondencia que vincula algunos elementos de un conjunto a algunos elementos de otro conjunto. Imaginemos que el conjunto C engloba todas las vocales del castellano, y el conjunto D los cinco primeros números enteros, de forma que C = {a, e, i, o, u} y D = {1, 2, 3, 4, 5}. Podríamos expresar la relación entre estos dos conjuntos vinculando arbitrariamente—en función de lo que queramos formalizar—algunos elementos de C, a algunos elementos de D, tal que obtendríamos una serie de pares ordenados que contienen un elemento de C y otro de D. De este modo, una relación entre C y D podría formalizarse así:
R ⊆ C x D = {(a, 1),(e, 2), (i, 3), (o, 4), (u, 5)}
Es importante fijarse en que esta relación no representa necesariamente todas las formas posibles de asociar los pares ordenados. Podríamos haber vinculado la ‘a’ al 3, y la ‘o’ al 1, pero en esta relación no hemos querido hacerlo así. Al conjunto de todos los pares ordenados posibles que pueden ser formados a partir de los elementos de dos (o más) conjuntos se le llama producto cartesiano, y se denota con C x D en nuestro caso. Nuestra relación R debe estar contenida o ser igual al producto cartesiano, lo cual se simboliza como R ⊆ C x D.
Ahora viene la parte interesante. Podemos considerar el lenguaje como la relación entre dos conjuntos A y B en el que A representa todos los objetos y conceptos que existen y B representa todos los símbolos y nombres que se utilizan para representar los conceptos y objetos del conjunto A. Llamaremos a esa relación L. El producto cartesiano de A y B incluiría todas las combinaciones posibles de nombres e ideas, tengan o no sentido. Por ejemplo (prototipo de gato, “almíbar”) y (luna, “pepino”) formarían parte del producto cartesiano, pero estarían fuera de nuestra relación, porque “almíbar” es una palabra que no se refiere al prototipo de gato y “pepino” otra que no se refiere a la luna. Nuestra relación entonces incluiría solo aquellos pares ordenados del producto cartesiano que tengan sentido, de forma que L ⊆ A x B. Una pequeña muestra de esto puede verse en el siguiente gráfico:
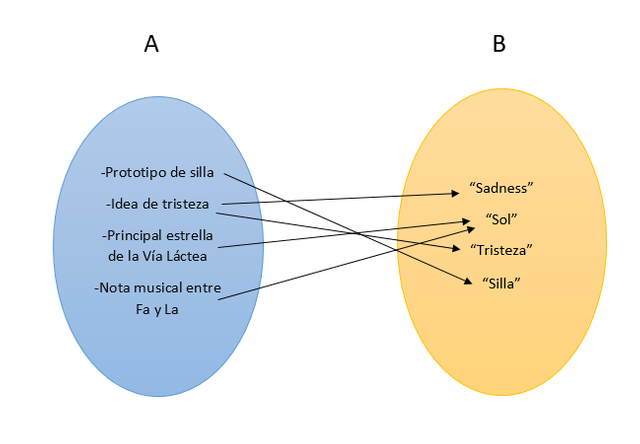
Vemos que más de un elemento en A tiene la misma correspondencia en B y que más de un elemento en B tiene la misma correspondencia en A. Esto da lugar a los conceptos de polisemia y heteronimia. La polisemia se da cuando un elemento del conjunto B se vincula a varios elementos diferentes del conjunto A; y la heteronimia se da cuando varios elementos del conjunto B se vinculan a uno del conjunto A. Es importante fijarse en que no puede haber ningún elemento en B que no tenga una correspondencia en A, ya que no existe ningún nombre que no denote nada; en el caso contrario, sí puede existir un elemento de A que no tenga una correspondencia en B, ya que no todo es explicable mediante el lenguaje.
En fin, el lenguaje también es una relación matemática entre dos conjuntos. Y sí, esto son mates aunque no haya calculado ninguna derivada parcial ni haya resuelto ni una sola suma.
Recuperado de mi blog: https://noostalgia.com/2016/06/05/el-lenguaje-como-relacion-matematica/
curiosamente, recuerdo haber leído que es un error considerar es un error considerar que un hemisferio cerebral es matemático y otro lingüístico, sino que las áreas del lenguaje parecían estar relacionadas directamente con aquellas de función matemática.
Que interesante artículo, quizá soporta esa idea? Un saludo!
¡Gracias por tu comentario!
Así es. La especialización de los dos hemisferios cerebrales es un mito muy extendido, aunque supongo que como psicólogo clínico ya lo sabes. Ambos se encargan de procesar el lenguaje y las matemáticas, solo que de diferente forma. Al fin y al cabo las matemáticas son un lenguaje universal cuyos referentes son abstractos, así que tiene sentido que tanto los lenguajes naturales como los simbólicos se procesen de manera parecida.
Me alegro de que te haya gustado el post.
Un saludo
Great content
But cheetah surveillance on u
Be aware
Thank you, but there's no reason why there should be any surveillance whatsoever on me, because all my posts are exclusively mine.
Es interesante verlo de esto modo!
Muchas gracias, David :)
Odiada por pocos, amada por muchos. Lo mejor que nos ha podido pasar!
¿Odiada por pocos?
Si te refieres a la matemática, creo que es al revés :)
Heyy, qué gran análisis que hiciste ahí. Me encanta cómo relacionaste ambas cosas de forma tan ordenada y sencilla. Saludos!
¡Me alegro de que te haya gustado, Daniela!
Un saludo