Serendipity en la geometría / Las geometrías no euclidianas

En días pasados leí un interesante post escrito por @alexandermoreno que explicaba el interesante tema de la serendipia.

Señalaba @alexandermoreno:

La serendipia es la aparición en el marco de una situación formal o informal de indagación, de un elemento no previsto el cual es el que, a final de cuentas, determina tal situación. Serendipia (serendipity, en inglés) es, entonces, el factor sorpresa por excelencia en los procesos de búsqueda de causas…

@alexandermoreno también citó una serie de importantes ejemplos, donde como resultado de una serendipia se habían dado solución a una serie de problemas en el mundo científico, entre ellos el descubrimiento de la penicilina y el de la viagra.

Motivada por este tema, decidí llevarlo al contexto matemático y conseguir un ejemplo donde la serendipia haya permitido un aporte importante a la matemática, y en efecto conseguí muchos, entre ellos el de las geometrías no euclidianas, las cuales son una serendipia que resultó de la imposibilidad de demostrar el quinto postulado de Euclides.

Fuente

Euclides quiso formalizar la geometría a través de cinco postulados que escribió en su libro Los Elementos por allá por el año 300 A.c., para ello escribió cinco postulados los cuales aplicó de manera exitosa a la geometría, es por ello que recibe el nombre de geometría euclidiana. De los cinco postulados, el número 5 es el más complejo, por ello se tendió a demostrar a través del proceso deductivo, usando los cuatro anteriores como premisas. Esta labor fue totalmente infructuosa, durante más de 2000 años, matemáticos conocidos trataron de hacerlo, llegando a resultados que dejaban de lado, pues lo único que buscaban era llegar a probarlo.

Pero a principio del siglo XIX, el quinto postulado fue refutado por diferentes matemáticos, entre ellos: Gauss, Lobachevsky y János Bolyai quienes demostraron que era imposible deducirlo de los cuatro postulados anteriores. Los resultados obtenidos a través de esta refutación los condujeron a otras geometrías, las geometrías no euclidianas.

La primera en aparecer fue la geometría hiperbólica, descubierta por Gauss (1777-1855), y de manera independiente de Gauss, lo hicieron Lobachevsky (1792-1856), János Bolyai y Ferdinand Schweickard. Posteriormente apareció la geometría elíptica.

Veamos a continuación los postulados de Euclides

Dos puntos cualesquiera determinan un segmento de recta.
Un segmento de recta se puede extender indefinidamente en una línea recta.
Se puede trazar una circunferencia dados un centro y un radio cualquiera.
Todos los ángulos rectos son iguales entre sí.
Postulado de las paralelas. Si una línea recta corta a otras dos, de tal manera que la suma de los dos ángulos interiores del mismo lado sea menor que dos rectos, las otras dos rectas se cortan, al prolongarlas, por el lado en el que están los ángulos menores que dos rectos.

Fuente

Estas geometrías cumplen con los cuatro primeros postulados de la geometría euclidiana, pero difieren en el quinto postulado. Esta diferencia se traduce en concepto matemático llamado curvatura.

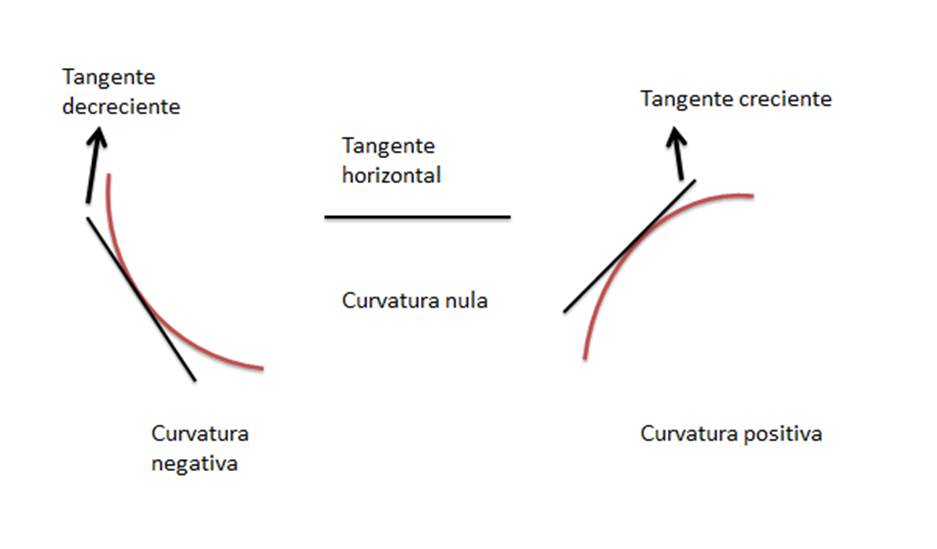
La curvatura es una medida del cambio de dirección del vector tangente a una curva, cuanto más rápido cambia éste a medida que nos desplazamos a lo largo de la curva, se dice que es más grande la curvatura.

Fuente

Veamos tal explicación en la siguiente imagen:

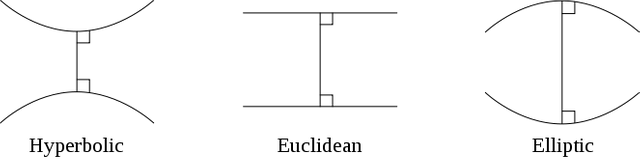
En esta imagen se muestran las tres geometrías en un campo homogéneo donde la la curvatura del espacio es la misma en cada punto.

Fuente

Si los espacios no son homogéneos, entonces podríamos afirmar que existen una infinidad de geometrías no euclidianas