Los monstruos de Cantor / La geometría fractal
La historia de los fractales es un cuento como el de la Bella y la Bestia. Los fractales fueron considerados monstruosos por los matemáticos de la época en que fueron creados, pero posteriormente resultaron ser bellos y útiles ampliando así el rango del conocimiento matemático por su aplicación en la naturaleza.

El matemático ruso Georg Ferdinand Ludwig Philipp Cantor (1845- 1918) acostumbraba escribirle cartas a Dedekind acerca de sus trabajos matemáticos. En una de ellas con fecha del 20 de junio de 1877, le expuso sus dudas acerca de la geometría en cuanto a la noción de dimensión. En matemática, este término intuitivamente se refiere al número mínimo de coordenadas que se necesitan para especificar la posición de un punto; por ejemplo un punto en una recta está especificado en una dimensión.
Ese término que todos manejamos y que además nos parece tan comprensible, a Cantor no le convencía, por ello comenzó con una indagación que lo llevó a un tipo extraño de geometría basándose en la naturaleza. Comenzó a tomar como modelos cosas que él veía en la naturaleza con ciertos patrones, como por ejemplo las aguas turbulentas, la anatomía, la botánica; y en muchas más cosas en las diferentes áreas.
También en Italia había otro matemático inquieto por el asunto, se trataba del matemático y filósofo italiano Giuseppe Peano (1858 -1932) quien en 1890 exponía sus ideas sobre algunas curvas que rellenaban un espacio cuadrado. A esas figuras geométricas creadas por Cantor y Peano se las consideró como monstruos sin utilidad en esos tiempos.
Pero a finales del siglo XVIII y principios del siglo XIX, Cantor y von Koch siguieron creando monstruos (más adelante voy a colocar un ejemplo de un monstruo creado por von Koch, llamado Copo de Nieve).
Interesadisimo en este tema el matemático polaco Benoît Mandelbrot (Varsovia, 1924) hizo un extenso estudio sobre esos "monstruos" y fue él quien los bautizó con el nombre de fractales, ya que presentan una forma irregular o fragmentada.
Señala Mandelbrot que
…se les puede calificar de “quimeras”, pues son “figuras intermedias” entre puntos y líneas, líneas y superficies, o superficies y volúmenes.
Y que por ello
Las bautiza como “fractales”…un avatar “monstruoso” de la noción de dimensión…”
Es importante resaltar que Benoît Mandelbrot hace un extenso análisis de todas las curvas de Peano, y consigue en ellas belleza y utilidad, por ello se pregunta ¿Cómo pueden ser algo monstruoso los fractales, si pueden ser bellos y de gran utilidad?
Veamos un ejemplo de su análisis correspondiente a las curvas aproximadas de Peano.
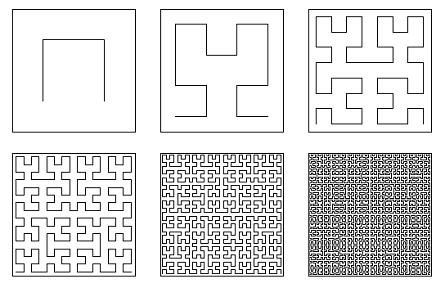
Veamos los collares de Peano que se hacen en la actualidad usando como modelo la curva de Peano anterior:

Veamos un ejemplo de cómo se construye un fractal.
El copo de nieve de Koch es una de las más sencillas figuras fractales, y una de las primeras. Fue inventada por el matemático sueco Helge von Koch en 1906.
Su construcción es como sigue: Se toma un segmento, se lo divide en tres partes iguales, se reemplaza la parte central por dos partes de igual longitud haciendo un ángulo de π/3 radianes (60 grados). Luego, con los cuatro segmentos, se procede de la misma manera, lo que da 16 segmentos pequeños. Y así sucesivamente, sin nunca parar. La figura representa las seis primeras etapas de la construcción. La última curva es una buena aproximación de la curva final.
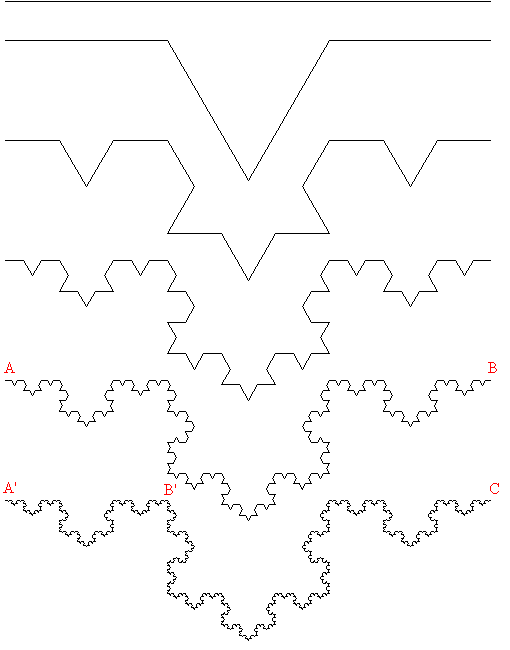
===================================
Referencia: Benoît Mandelbrot en Pensar la Matemática. Tusquets editores S.A. Barcelona, 1982.
Oh vaya que interesante tema aprendí mucho lo qiw confirma que todo se intwerelaciona asi algo tan preciso como las matemáticas tienen su fractal en la estética y por ende en la belleza
Gracias @sincroniadivina. Muy agradable tu comentario, me gusta que mis post sean de utilidad. Saludos.
Como decia voltaire
Muy acertado tu comentario. Gracias.
Interesante historia
Me alegra que haya parecido interesante mi post. Abrazos.
No hay duda que los fractales poseen un interés de carácter matemático (geométrico) y también de carácter estético, todo lo cual plantea relevancia. Gracias por su post toda vez que revela la precitada coexistencia.
Gracias @alexandermoreno.
This post has received a 0.65 % upvote from @drotto thanks to: @analealsuarez.
You got a 2.56% upvote from @getboost courtesy of @analealsuarez!
You got a 19.59% upvote from @nado.bot courtesy of @analealsuarez!
Send at least 0.1 SBD to participate in bid and get upvote of 0%-100% with full voting power.