Conjuntos numéricos/ El conjunto de los números reales R.
Uno de los aspectos matemáticos que tienden a confundir más a las personas en general, son los conjuntos numéricos. La gente no sabe clasificar los números, no sabe diferenciar por ejemplo, un número entero de un número racional, o número racional de un número irracional, en fin; bueno, me parece pertinente aclarar este punto; y en ese sentido va orientado el siguiente artículo.
¿Qué es un conjunto numérico?
Comencemos por explicar lo que es un conjunto numérico; un conjunto numérico es una colección de números vinculados por una relación entre ellos, una categoría común que los vincula; por el ejemplo el conjunto de los números pares, se entiende que en este conjunto deben ir todos los números que son múltiplos de 2 (esta es la categoría que los vincula), por ejemplo el mismo 2, el 4 y así sucesivamente; para expresarlo como conjunto, se deben colocar sus elementos entre llaves, lo cual significa pertenencia al conjunto, y además, colocarle un nombre, el cual puede ser una letra mayúscula, por ejemplo M, P, Q,… , vamos a elegir M como nombre para nuestro conjunto, entonces particularmente el conjunto queda expresado así:
M= {…-6, -4, -2, 0, 2, 4, 6…}, los puntos suspensivos indican que nuestro conjunto es infinito tanto por el lado negativo (- ∞) como por el lado positivo (+ ∞).
Conocidos estos aspectos, ahora podemos hacer uso de algunos símbolos utilizados en matemática, particularmente, el símbolo de pertenencia.
El símbolo de pertenencia se denota mediante la letra griega "∈", es la quinta letra del alfabeto griego llamada épsilon, y se utiliza para denotar que un número x (cualquiera) pertenece a un conjunto A cualquiera. Por ejemplo, si continuamos con nuestro ejemplo, 4 ∈ M se lee “4 pertenece a M”, lo cual es una proposición verdadera, pero
7 ∈ M es una proposición falsa ya que 7 no es un número par, en este caso escribimos 7∉ M.
Conjuntos numéricos básicos.
Comencemos ahora con los conjuntos numéricos básicos, llamémosles así para diferenciarlos de ejemplos como el anterior, los cuales vendrían a ser subconjuntos de algunos de los conjuntos que ahora vamos a estudiar.
El conjunto de los números naturales.
El conjunto de los números naturales, denotado por la letra "ℕ", es el conjunto conformado por los números que usamos para contar, y con el cual hacemos operaciones básicas, este conjunto se inicia desde el 0, que denota ausencia de objetos, seguido del 1, 2, y así sucesivamente. La regla que los vincula como conjunto es que si tenemos un elemento x en ese conjunto, también estará su sucesor x+1.
Y así
ℕ= {0, 0+1, 0+1+1, 0+1+1+1, 0+1+1+1+1 …}= {0, 1, 2, 3, 4….}
Donde se puede afirmar por ejemplo que 10 ∈ ℕ , pero -10 ∉ ℕ
El conjunto de los números enteros
Es importante destacar que en el conjunto de los números naturales se realizan operaciones elementales, esto es, dados cualquier par de números naturales a y b, se puede obtener a+ b, y a. b (como una suma abreviada); pero no siempre se puede realizar la operación a - b, ésta se puede realizar solo si se cumple que a ≥ b (que el minuendo sea mayor o igual que el sustraendo), esto es "si a es mayor o igual que b". Por ejemplo, si se quiere realizar en el conjunto de los números naturales, la operación 5-8, no vamos a conseguir su resultado en ese conjunto.
Esto demostró que el conjunto de los números naturales es incompleto, y que por ello, hay la necesidad de ampliar este conjunto, bajo esa idea, se le agregó una parte negativa a este conjunto, de tal forma que cada número natural distinto a "0", posee un correlato negativo; a este conjunto ampliado se le llamó ℤ, el conjunto de los números enteros. De tal forma que se crea un nuevo conjunto que tiene dos grupos de números, los enteros positivos y los enteros negativos, y un elemento neutro, el 0, el cual no es ni negativo ni positivo.
ℤ= {…-4, -3, -2, -1 , 0, 1, 2, 3, 4…}
Obsérvese que todo número natural es un número entero, pero no todo número entero es natural, por eso se dice que ℕ C ℤ, esto es “ℕ es subconjunto de ℤ”.
En este nuevo conjunto se resuelve el problema de operaciones de sustracción donde el minuendo es menor que el sustraendo, y así el resultado de "5 – 8", es -3, el cual pertenece a ℤ (-3 ∈ ℤ).
Solucionado el problema de la sustracción, se presenta un nuevo problema, y es el de la división, en este conjunto la operación de división está restringida solo a enteros divisibles exactamente, esto es, divisiones exactas como -10/5= -2, pero divisiones como 5/-10 son imposibles de realizar en este conjunto.
Debido a la restricción de la división en "ℤ", se hace necesario ampliarlo, agregando todos los posibles resultados de dividir "a/b", donde "a" es cualquier número entero, y "b" es un número entero diferente de 0.
El conjunto de los números racionales
Este nuevo conjunto se llama Q, "el conjunto de los números racionales",el significado de racional viene de razón que en matemática significa "dividir".
Luego
Q= { a/b / a ∈ ℤ y b ∈ ℤ * } donde ℤ* es el conjunto de los números enteros diferentes de 0.
Ejemplos de números racionales son:
10/(-5)= -2 , observe que este resultado es también un número entero, por lo cual se puede afirmar que todo número entero es un número racional, pero no todo número racional es un número entero, veámoslo en el siguiente ejemplo: (-5)/10= -0,5. Esto significa que ℤ C Q.
Otros ejemplos importantes son:
1/7=0.142857142857142857… Una expresión decimal ilimitada periódica, de periodo 142857
3/5=0,60000000…. También es una expresión decimal ilimitada periódica, de periodo 0.
Lo cual también se cumple en el siguiente ejemplo -2=(-2)/1=-2,000…
Y así sucesivamente, la categoría que caracteriza a los números racionales, es que "consisten en expresiones decimales ilimitadas de tipo periódica".
Hasta ahora hemos logrado superar las dificultades que se nos han presentado en cada conjunto por su incompletitud, y da la impresión que la labor se ha concluido, pero no, hay más.
El conjunto de los números irracionales.
Observe el siguiente triángulo rectángulo, la longitud |AB| es igual a la longitud de |BC|, ambos segmentos son catetos del triángulo ABC, supongamos que |AB|= |BC| igual a 1, entonces para obtener la longitud de la hipotenusa |AC|, aplicamos el Teorema de Pitágoras, esto es:
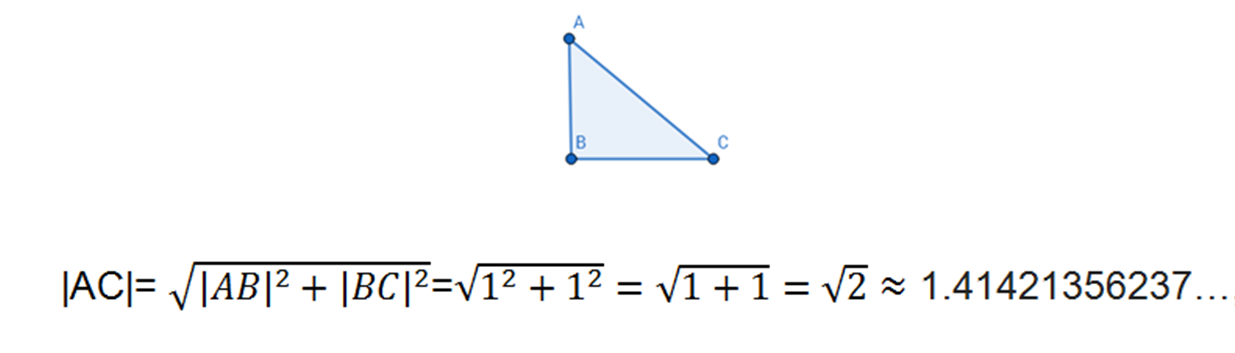
Este resultado es una expresión decimal ilimitada no periódica, busque √2 en cualquier calculadora que tenga capacidad de dígitos superior a la utilizada para calcular este resultado, y se observará, que no existe un patrón de repetición en los caracteres decimales. Otro aspecto importante a destacar es, que este resultado no se obtuvo de la división de dos números enteros. Estos dos aspectos indican que se está tratando con un número no racional.
Existen otros números como este, por ejemplo el número e, base de los logaritmos neperianos, busquemos en la calculadora su expresión numérica, y observaremos que corresponde a 2,71828182846… (Este resultado es una expresión decimal ilimitada, no periódica), el cual se obtiene del siguiente límite:
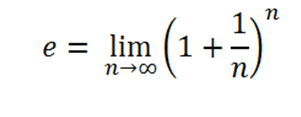
También π, es un ejemplo de este tipo de números, recuerde que π, es la constante que vincula la longitud de una circunferencia con su diámetro., π ≈ 3,14159265359…
Este tipo de números se llaman irracionales (Irracionales, porque no se obtienen como resultado de una división de enteros). Existen infinidad de ejemplos de este tipo de números, ellos conforman el conjunto de los números irracionales I .
Obsérvese que al final tenemos dos grandes conjuntos, los racionales Q y los irracionales I, donde, entre ellos no hay elementos comunes, esto es, un número racional no puede ser irracional y viceversa.
De la unión "U" de estos dos grandes conjuntos se obtiene un gran conjunto:
El conjunto de los números reales R.
Este es:
En este conjunto tenemos garantizadas todas las operaciones básicas, y es el conjunto donde se fundamenta la matemática que manejamos comúnmente, sin olvidar que hay algo más allá, y es que en este conjunto no se puede realizar la operación √(-1), es aquí donde falla R, y hace su aparición el conjunto de los números complejos. El cual estudiaremos en otra oportunidad.