How The Stars Work - Part 2: The star energy source

In the first part ( how the star works - Part 1: Gravity and Gas Pressure ), we already know why stars remained stable for billions of years, that is, because of the equilibrium between gravity and thermal stress or radiation pressure.
We can see also where the emergence of the force of gravity, but the exposure in the first part even raises a new question: where does the radiation pressure come from? Of course, the radiation pressure is generated by the generation of energy in stars. Stars produce energy which then produces radiation pressure to balance the star. But again, where is the star energy? This is an ancient mystery that takes a long time to answer.
Energy from shrinking the Sun?
In the 19th century, two great physicists, Lord Kelvin of England and Hermann von Helmholtz of Germany separately tried to answer this question: What if the solar energy comes from the shrinkage? Suppose in the past the size of the sun is much greater than its present size. Then slowly, the sun shrinks because of the gravitational pull of its mass. This shrinking will free up potential energy that can be converted into thermal energy. What is the potential energy released by the Sun? Had the sun in the past had fingers far larger than its present fingers, the shrinking of the Sun had liberated the potential energy of 4 x 1048 erg. According to the virial theorem, when a gravity system (like the Sun) changes its equilibrium, half of its potential energy will be converted into thermal energy, while the other half will be emitted. Thus, the energy emitted by the sun is 2 x 1048 erg. This energy is huge, but is this the source of solar energy?
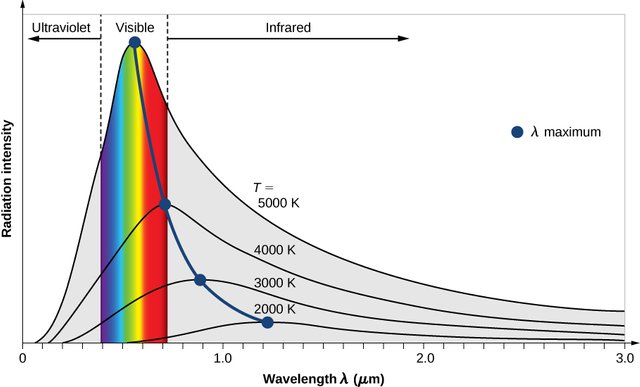
Curve distribution of the energy intensity of a black body. Credit image
To answer this question, we need to know how much energy the sun emits every second. This can be calculated if we, again, assume the sun as a perfectly fluorescent black body. With this supposition, the curve of the energy distribution of a black body can be used to calculate the energy output of the black body throughout the wavelength, then summing all the energy at different wavelengths. From this procedure, we will obtain a law called the Law of Stefan-Boltzmann, which states that the total energy of every second emitted from every unit of the surface area of a black body is only dependent on its temperature. Since we know how much the surface of the Sun (assuming the Sun is spherical with the radius of 700,000 km) and also its surface temperature is 5800 K, it can be calculated the total energy radiating from the entire surface of the Sun at this time is 3.8 x 1033 erg per second! This equals 3.8 x 1026 Watts. Imagine how many houses can be illuminated by the Sun's energy when every home needs 1000 Watt of power. Of course, this energy radiates in all directions and only 1400 Watt per square meter reaches Earth.
Now we know that the Sun emits 3.8 x 1033 erg energy every second and that the total energy generated from the gravitational pull is 2 x 1048 erg. Had the sun radiated its energy constantly and unchanged, this gravitational shrinking had lasted for about 17 million years. From the signs of life on Earth, we have realized life has lasted 3 billion years, while the Kelvin-Helmholtz shrinking is only capable of producing comparable energy in the tens of millions of years. So, there must be another energy source that can generate energy on a scale of 1033 erg for billions of years.
Radioactivity
Another alternative to answering this problem is through radioactive phenomena. In 1896, Henri Becquerel discovered the phenomenon of radioactivity. Heavy atoms such as Uranium have radioactive properties, and these atoms emit enormous amounts of energy in the form of radiation. Why is that? No one understands. The Pierre and Marie Curie spouses tried to answer this question and paid for it with their lives. Their interaction with radioactive materials was so close, and at that time, the dangers of nuclear radiation had not been realized. Their research records have become so radioactive after years of exposure to Radium radiation, so until now, they should be stored in tin-lined boxes. Marie Curie died of leukemia, after years of researching the phenomenon of radioactivity and in contact with radiation. However, the sacrifices of Pierre and Marie experimenting in their small laboratory in Paris show the enormous source of energy in the atom.
How can this energy source be generated? No one understands what actually happens inside the atom. At the end of the nineteenth century, physicists envisioned atoms just like a simple positive ball and in them, the negatively charged electrons were evenly distributed and neutralized the proton's positive charge. Such a model, for example, is the J.J raisin cake model. Thomson. However, this structure is unable to explain the phenomenon of radioactivity. Further experiments by Ernest Rutherford and Hans Geiger and Ernest Marsden show that all the protons in the atoms are concentrated in a positively charged nucleus, and this nucleus is surrounded by electrons. The most surprising of Rutherford's experiments is that the diameter of this nucleus is 100 000 times smaller than the diameter of the atom. If we imagine a ping pong-sized atomic nucleus, the electrons would orbit the atom's nucleus about 500 meters from the ping pong ball! This is very unusual. Everything we can touch, grasp and feel, is made up of empty space!

Pierre and Marie Curie's research shows the radioactivity phenomenon that frees up enormous amounts of energy. Credit image
The electrons are bound by the nucleus of the atom because of the electric force of attraction between the negative charge contained in the electrons and the positively charged nucleus. Rutherford shows that the atomic nucleus is made up of positively charged protons, and each atom has the same number of protons and electrons. Thus, the total amount of charge is zero and we can say that the atom is neutral. Later, Rutherford's student, James Chadwick, discovered that in the nucleus there are also uncharged neutrons.
Given this understanding of atomic structure, physicists began to understand the radioactivity phenomena found by Becquerel, Pierre Curie, and Marie Curie. An element can be transformed into another element because of changes in the number of protons and electrons in the atom. In each atom is contained the number of protons and specific electrons possessed only by these atoms, and when the protons and electrons are exchanged, then an atomic nucleus can be transformed into another nucleus of atoms.
One example is Radium studied by Pierre and Marie Curie. Radium has 88 protons and 138 neutrons. This amount is quite large and tends to be unstable and can be transformed into other elements. In the case of Radium, 2 protons and 2 neutrons can be released so that it becomes Radon with 86 protons and 136 neutrons. Combined 2 protons and 2 neutrons are called Alpha particles. This is the radiation that slowly kills Marie Curie. The reaction of breaking a large element into a small element is called a fission reaction and is the working mechanism behind atom bombs or nuclear reactors. Heavy atoms such as Radium are relatively unstable and will release alpha particles by themselves through a phenomenon called decay.
Could it be that the opposite reaction, which is merging two small atoms, can produce energy? Hydrogen has only 1 proton and is the simplest atom in terms of its proton and electron arrangement. Theoretically, the incorporation of 2 Hydrogen atoms into Helium with 2 protons is possible. This is called a fusion reaction. Through spectroscopic observations, we know that Hydrogen and Helium are the two most abundant elements in the star. So, is it possible that the Sun generates its energy through fusion reactions?
Hydrogen is a relatively stable atom, therefore-unlike a decaying heavy atom-the fusion reaction does not happen by itself. There must be a condition that is very extreme. Under these conditions, Hydrogen can melt into Helium. This extreme condition requires very high temperatures and pressures. In the first part we already know that there is a gravitational pressure of greater magnitude as we get closer to the center of the star. Is it possible that in the center of the star, the pressure of gravity and temperature is so great that the fusion reaction can occur?
In the first part we already assume the Sun is in equilibrium between the gravitational pressure and the radiation pressure, an equilibrium we call the hydrostatic equilibrium. Armed with this assumption, we can calculate the gravitational pressure occurring in the center of the sun, ie 3.4 × 10 {11} atm or approximately 340 billion times our atmospheric pressure! If we suppose that the gas in the center of the sun is the ideal gas, then the ideal gas law allows us to calculate the temperature in the "stove" of the sun if we know how much pressure in the center of the sun. The temperature in the "furnace" of the sun is thus roughly 15 million Kelvin!
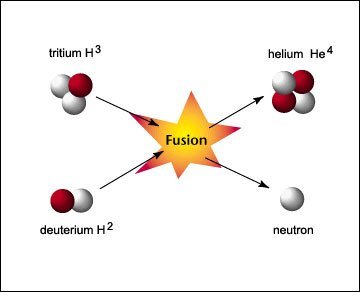
A simple fusion reaction occurs by combining four Hydrogen atoms into 1 Helium atom. Credit image
These temperatures and pressures are very high and allow for fusion reactions. How much energy is liberated by this reaction? From the experiment, it is known that the mass of 1 Helium atom is slightly lighter than the mass of 4 Hydrogen atoms. There is a mass loss of 0.7% of the mass of 4 Hydrogen atoms, meaning that every 1 kg of Hydrogen will change to 0.993 kg of Helium, and the remaining mass loss of 0.007 kg will be converted into energy. How much energy is liberated by 0.007 kg of this mass? When Enstein examines the effects of special relativity, he finds that the energy (E) and mass (m) are apparently equivalent and can mutually change through the very famous equation, E = mc2, where c is the speed of light. The speed of light is 300 000 km per second (3 x 108 meters per second), a very high speed. Thus a small amount of mass can be converted into an enormous amount of energy, due to the enormous conversion factor of c 2. Through this very famous formula of Enstein, we can calculate that the reaction of 1 kg of Hydrogen to 0.993 kg Helium will free the mass of 0.007 kg equivalent to the energy of 0.007 x (3 x 10 8)2 = 6.3 x 1014 Joule energy. This is proportional to the energy produced by burning 100 000 tons of coal!
Enough of this enormous energy to support the Sun? We know that the amount of Hydrogen in the Sun is about 75% of the total mass of the Sun. We can calculate how much energy will be released if 10% of this Hydrogen is melted into Helium:
Energy = 0.007 x 0.75 x 0.1 x (2 x 1030) kg x (3 x 108 m / s)2 = 9.4 x 1043 Joule = 9.4 x 1050 Erg.
A tremendous energy, almost a thousand times the energy liberated by gravitational shrinking! How long can this nuclear reaction support the Sun? As we know, the energy emitted by the Sun is 3.8 x 1026 Joules every second. This means the Sun can shine over 7.5 Billion years!
This number is quite consistent with what we know. Allegedly, the Sun and our solar system formed between 4 to 5 billion years ago. A more rigorous modern calculation concludes that the area inside the Sun that is hot enough to produce a nuclear reaction is only an area that accounts for 10% of the total Hydrogen in the Sun, as we calculated above. Furthermore, the duration of burning Hydrogen into Helium is approximately 10 billion years. So, the Sun that is currently 5 billion years old is in middle age and will still shine up to 5 billion years.
Thus, in this section, we have concluded that the Sun generates its energy from the fusion reaction. The fusion reaction is a reaction that combines small atoms into large atoms, in which case it is the fusion of 4 Hydrogen atoms into 1 Helium atom. Our calculations of pressure and temperature in the core of the Sun also conclude that the pressure and temperature in the core are hot and solid enough to trigger fusion reactions.
However, what exactly does this reaction look like? Extreme conditions that can produce fusion reactions are very difficult to create on Earth. Simulating the core of the sun with the pressure of hundreds of billions of times the Earth's atmospheric pressure and the temperature of 15 million Kelvins is very difficult. The only way to fathom the details of nuclear reactions in the "furnace" of the Sun is by way of theoretical calculations, then comparing them with what we observe on the surface of the Sun. This is a difficult job and will be told in the next section.



the information that really useful! this motivate me want to be astronauts and go to the space to see how the beauty of the universe is filled with star star
hopefully can be realized what you want