nanotecnology age (Carbon Nanotubes)

At the beginning of the decade of the 90 S. Iijima investigating on the fullerenes, observed by means of a transmission electron microscope (TEM) carbon nanotubes (NTsC) [1], which constitute a new allotropic form of coal (figure 1 ) [2].

                                                       

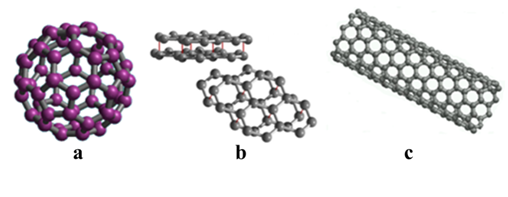
                                 Figure 1. Allotropic carbon forms: fullerene (a), graphite (b), carbon nanotube (c). 

Carbon nanotubes are cylindrical molecules composed of carbon atoms [3], which have diameters in the order of nanometers and lengths in the micrometer [4]. One of the most important feature is the hexagonal pattern that repeats periodically in space.3 This one-dimensional structure [5] is mainly due to the sp2 hybridization process, during which an orbital s and two orbital p are combined to form three sp2 hybrid orbitals at 120º With each other within a plane (figure 2a) [6]. These nanostructures are considered theoretically from a sheet of graphene wrapped around itself (Figure 2b) .[7]

                                        

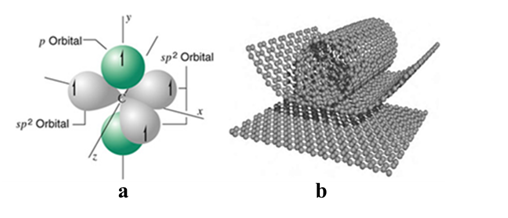
Figure 2. Sp2 hybridization present in carbon nanotubes (a). Single-wall carbon nanotube (NTsCPS) from a sheet of graphene (b).

Structure of carbon nanotubes.

There are several ways to identify a single structure for each carbon nanotube. One way is to think that each nanotube, results in winding a graphene sheet, specifying the direction of the winding and the circumference of the cross section. [6] In this sense, the atomic structure of carbon nanotubes is described in terms of chirality or (C ⃗h) and the chiral angle (θ). In figure 3 we visualize the cutting of a sheet of graphene along the dotted lines and how two atoms are chosen in The graphene sheet. The chiral vector starts from the first atom (taken as the origin) pointing to the second atom [5], when the leaf is wound up, the tip of the chiral vector touches the tail of vector [7]

                                                      

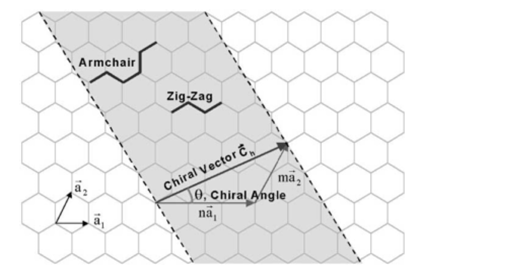
Figure 3. Diagram showing how a sheet of graphene is coiled to form a carbon nanotube.[7]

This vector is also known as winding vector [5] and can be expressed through the following equation:

                                                

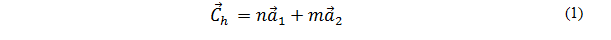
Where n and m (called Hamada8 index) are integers and represent the numbers of steps along the carbon bonds of the hexagonal network, 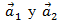    Are the unit vectors of the two-dimensional network [7]. The magnitude of the chiral vector represents the diameter of the nanotube [6] and is known by the following equation:

                                            

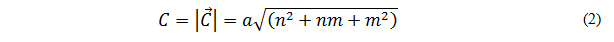
Where a is the magnitude of the unit vector 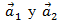Of the hexagonal network. [8]. This also represents the carbon-carbon bond length (    acc =1.42 Å     Measured by Spiers and Brown in 1996, then confirmed by Wilder in 19988) by the relationship. 

                                             

                                             

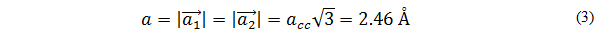
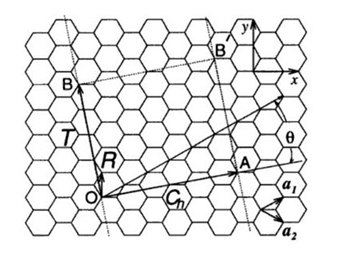
Figure 4. The unit cell of a single-walled carbon nanotube ( MWNT ) is given by the rectangle: O-B-B'-A.8

When viewing Figure 4, we observe that the perimeter of the base of the nanotube is given by the segment OA, which exactly matches the chiral vector module, so we can obtain the following expression for the radius of the nanotube [8].

                                           

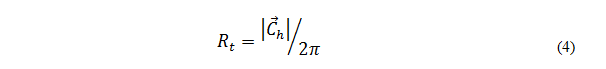
Substituting equation (2) into (4) we obtain:

                                          

On the other hand, the angle between the chiral vector 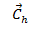and the unit vector 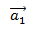is called the chiral angle (θ) (figure 3) [8], which gives us information on the torsion of the tube7 and is expressed as follows :

                                                   

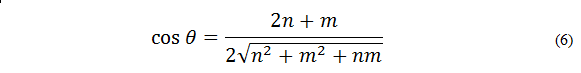
We can see in equation (6) that the chiral angle depends on the Hamada indices (n, m).

Reference

  (1)  González, R. M. Funcionalización de nanomateriales de carbono: Propiedades optoelectrónicas de nanotubos de carbono y aplicaciones de nanopartículas de diamante en catálisis y biocatálisis, Universidad Politécnica de Valencia, 2011. 

(2)  Hamada, N.; Sawada, S.; Oshiyama, A. Phys. Rev. Lett. 1992, 68 (10), 1579–1581. 

(3)  Ruoff, R. S.; Qian, D.; Liu, W. K. Comptes Rendus Phys. 2003, 4 (9), 993–1008.

 (4)  Kumar, M.; Ando, Y. J. Nanosci. Nanotechnol. 2010, 10 (6), 3739–3758. 

(5)  Belin, T.; Epron, F. Mater. Sci. Eng. B 2005, 119 (2), 105–118. 

(6)  Qian, D.; Wagner, G. J.; Liu, W. K.; Yu, M.-F.; Ruoff, R. S. Appl. Mech. Rev. 2002, 55 (6), 495–533.

 (7)  Thostenson, E. T.; Ren, Z.; Chou, T. 2001, 61, 1899–1912. 

(8)  QUISPE, F. A. ESTRUCTURA Y SINTESIS DE NANOTUBOS DE CARBONO, UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS, 2005.