Project // Omoikane's Legacy - Quantum Mechanics (Part I)
Project // Omoikane's Legacy
About Science and Philosophy.
Quantum Mechanics
Part I: A Historical Introduction to Quantum Physics
With few words, quantum mechanics is the theory that describes how particles behave and interact on very small scales. What happens in atoms? How do electrons look like? ... Despite common belief, the field of quantum mechanics is not as brain-twistingly complicated as people usually suppose. It is definitely true that quantum theory tends to escalate comparably quickly into an entangled mess of partial differential equations straight out of the seventh circle of hell. From personal experience, though, I can tell you, this is nothing in contrast to the horrifyingly gory index carnage that occurs within general relativity theory. However, the more import aspects are the underlying basic concepts, which in this case aren't nearly as devilish. In my humble opinion, the key of understanding a topic lies not within learning every little detail by heart, but understanding what is going on, on a fundamental level. Consequently, knowledge then results from the power of being able to deduce information, instead of just reproducing it. A good way of starting to explore a matter is to have a look at its history. So, let's follow the steps that led to the discovery and elaboration of quantum theory in this first of two parts about quantum mechanics.
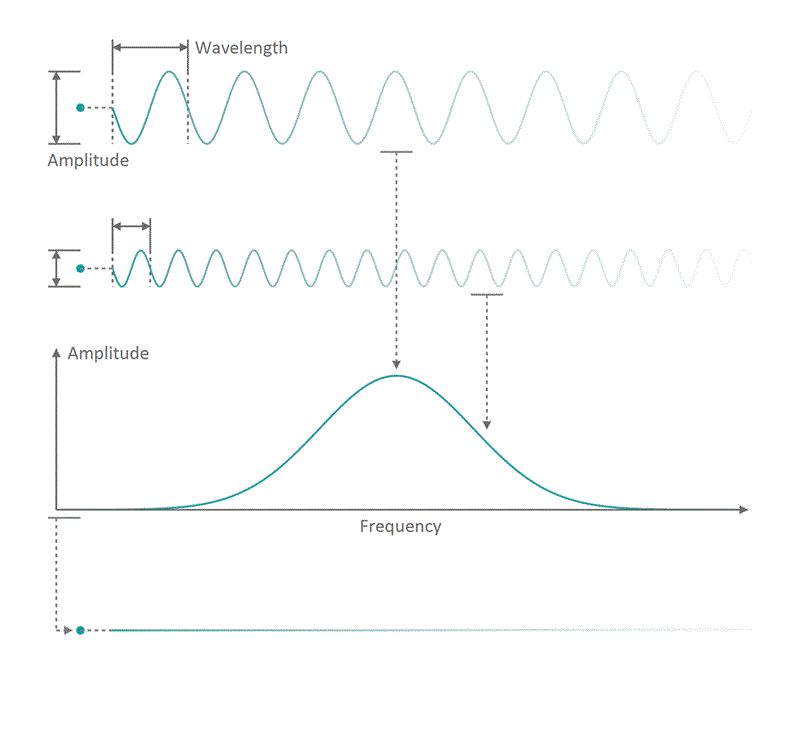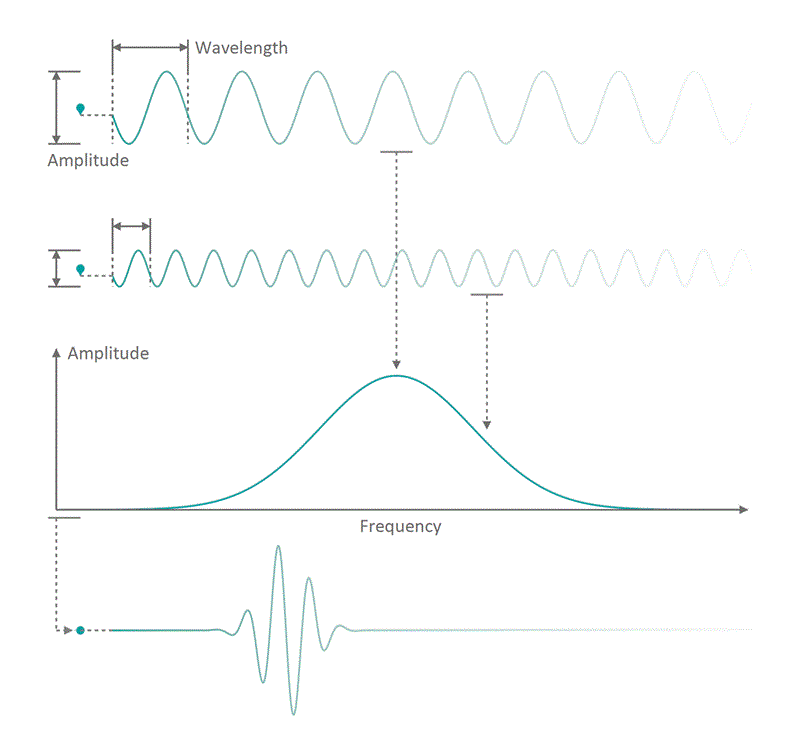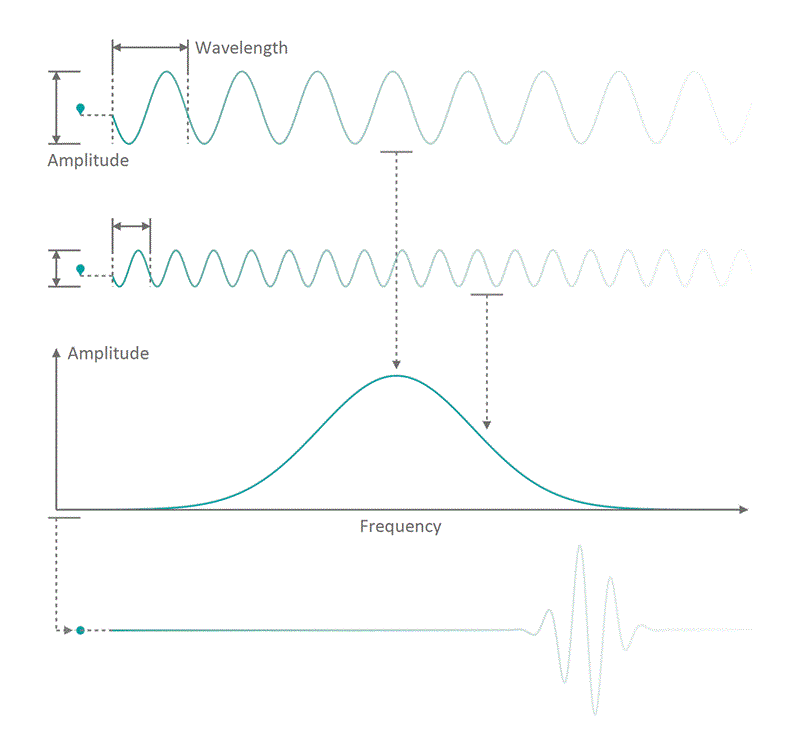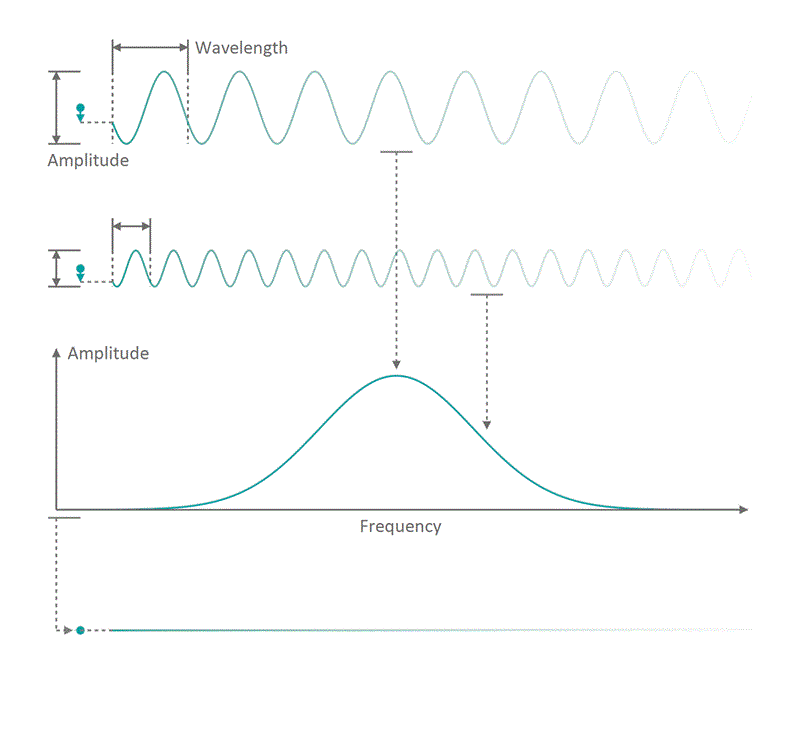
It all started in the early 20th century when people tried to understand electro-magnetic spectra resulting from different physical processes: Over a century ago, James Clerk Maxwell compiled his Maxwell equations, a collection of four equations that describe how electric and magnetic fields interact with each other through electric charges and currents. An intrinsic property which immediately arises from the correlations dictates that coupled fields of electric and magnetic nature start to propagate as waves, comparable to ripples on the surface of a lake. Depending on how fast the electric and magnetic field components oscillate while travelling through space and time, you can associate a frequency with the oscillation, similar to how sound waves carry tones of different pitch. Instead of describing a field using its temporal behavior (how its values change over time), you can understand it as a superposition of many oscillating components with different strength (amplitude) and oscillation speed (frequency). See figure 1 for a visualization. The functional dependence of the various oscillation amplitudes and their associated frequencies that make up a wave is called its spectrum. The so-called wavelength describes the distance, a wave has to travel until it performs a full oscillation period. It is proportional to the wave's propagation speed and inversely depending on the frequency. We are all very familiar with electro-magnetic waves since we literally see them every day... in fact we do see nothing but electro-magnetic waves as visible light itself is just a small frequency range in the electro-magnetic spectrum. The different frequencies of visible light waves correspond to the perceivable colors and everyone who has ever seen a rainbow knows that you can split light into its spectral components. In that sense, a rainbow is just a very colorful display of the sunlight's frequency spectrum. In many cases, observing and analyzing the spectrum of electro-magnetic waves (spectroscopy) that are emitted during a physical process, is the only way of gathering information about it.
People in 1900 were very aware of these principles when they studied a phenomenon called cavity radiation: You might have noticed that, when a material is heated up thoroughly enough, it will slowly start to glow red, then orange and finally bright white. This light emission is caused by an increasing movement of the particles our material is comprised of. Heating something means pushing energy into it. On an atomic level this energy is transferred to the individual electrons and nuclei which start jittering randomly as heat (thermal) energy is converted to movement (kinetic) energy. Perceivable 'temperature' itself is just a macroscopic measure for the average 'jittering strength' of the particles in an observed object. Charged particles, like electrons, moving to and fro create oscillating electric and magnetic fields which - as we have already learned - travel away in form of waves. This a) will lead to a loss of energy, cooling the material back down over time and b) explains the observed glowing. As red light has the lowest frequency compared to the other colors, it comes as no surprise that an object will begin to glow faintly red when heated up. This correlates with a slow average movement of the material's electrons. As more energy is available, some particles will be able to move faster, thus, higher frequency components will start to appear in the thermal radiation spectrum. All spectral components ultimately mingle into a bluish white light emission as can be seen in figure 2. Reversely, you can assign a temperature to light emission colors. When you are buying white LED lights for example, they will always have a color temperature (warm white ~2700K, cold white ~5000K, ...) associated with them, corresponding to the black body radiation hue. Now, imagine a hollow container (cavity), which is heated from outside. Through a small hole in the front, the thermal radiation inside can be observed. As light waves cannot exist inside the container's walls, their amplitudes have to be zero at the cavity boundaries. This behavior resembles vibrations in a rope that is fixed to the walls. Therefore, only oscillations with specific frequencies, matching the waves' length to the cavity's dimensions, can exist inside the container. Thermodynamics dictates that the energy content of each discrete frequency component must be in equilibrium with the thermal energy pushed into the cavity. However, when you just distribute the energy evenly over all available wave modes and try to calculate the resulting spectrum, things go wrong horribly. For low frequencies, everything is in good agreement with observations. However, with increasing frequency (corresponding to smaller wave lengths) you can find more and more ways to fit waves inside the cavity. Their spectral density (frequency components per range) increases and the overall spectral energy content in higher frequency modes shoots through the roof. Very figuratively, this behavior was named ultra violet catastrophe as it represents a solarium in overdrive mode, ripping every single connection between all particles to bits before you can say "ouch". Since we are not part of an infernal toaster oven, this approach is obviously wrong.
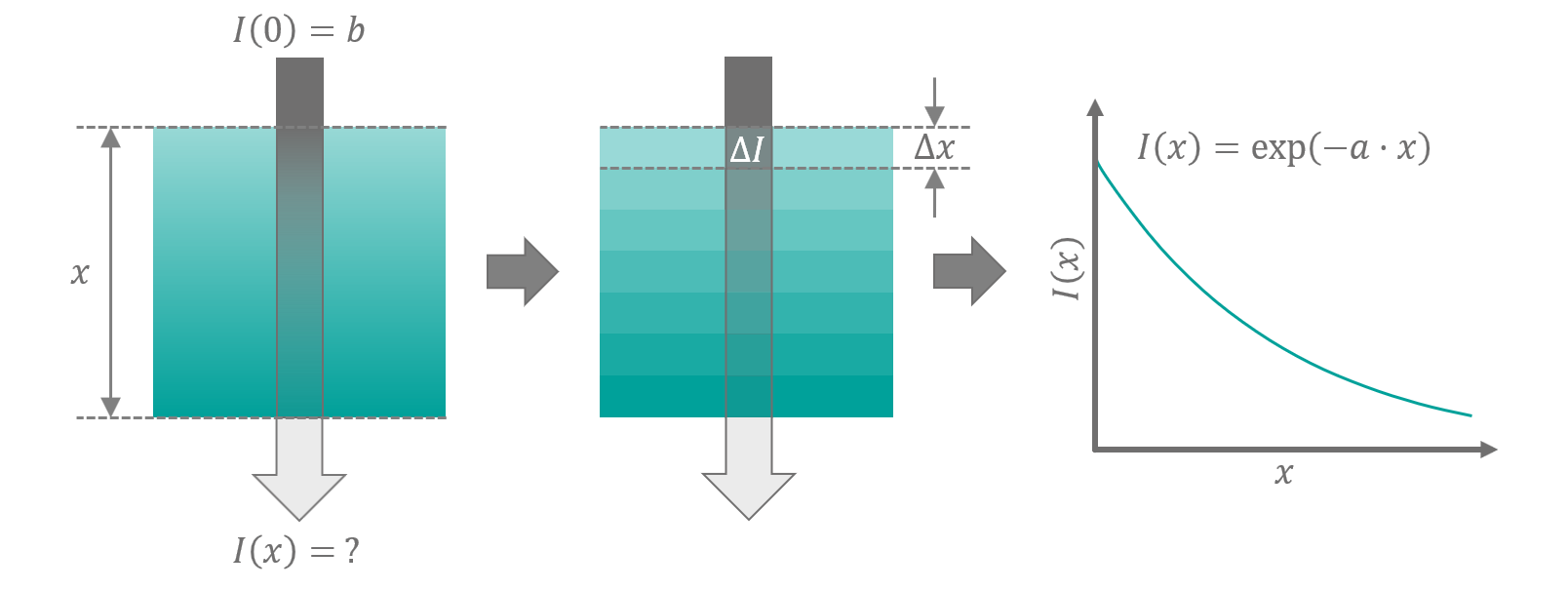
In 1905 Max Planck tried to solve the conundrum by applying all sorts of mathematical tricks to it. Let me explain to you, what exactly was involved in the approach that finally yielded a valid solution: Sometimes it is helpful to partition your problem into small sections, perform your calculations on the chunks and finally make your artificially introduced portions disappear by assuming they are infinitely small again (which means, the whole thing transitions back to being continuous like the original problem was). An intuitive example using this method is the derivation of light absorption in opaque media. When you want to know how much light is transmitted through a semi-transparent volume, you will find that the absorption strength at each point in the medium depends on the remaining intensity of the light. The more light is left, the more is lost. This dependence between the rate of change and the value itself makes it non-trivial to solve the problem directly. Instead of trying to find a solution for the whole block at once, imagine it being chopped into small slices with thickness Δx. We assume that our strips are thin enough, that their absorption behavior is approximately constant over their full diameter. Every slice will attenuate the light intensity by an amount ΔI proportional to the input intensity I, its thickness and a constant dampening factor a that only depends on the material:
See figure 3 for a sketch. This relation is applicable to every individual slice i with its respective intensity and attenuation (ΔIi, Ii). The balance of the equation stays preserved, when we sum over the terms of each left and right hand side for any number of slices N:
→ ∑0≤i<N (Ii-1·ΔIi) = -a·N·Δx
When we choose the number of plates such that they always assemble into a volume of material with a fixed total thickness x (N ≡ x/Δx) the right hand side of the equation becomes independent of how we partition the medium (-a·N·Δx ≡ -a·x). Now, we transition our setup back to a continuous problem by making the slices infinitesimal (infinitely thin), i.e. Δx → 0, N → ∞. The infinitely wide sum over infinitely small sections that occurs on the left hand side of the equation is known as a Riemann integral (denoted as ∫). Imagine it as an area consisting of infinitely small rectangles with area I-1·dI (dI is the notation for infinitesimal quantities). By adding these for each of the infinite points between 0 and x you will find the exact area below the graph of the function I-1. What is the results of ∫(I-1)dI? By using the powerful solving method of "already knowing the answer" I can tell you it is ln(I) + b̅ where ln(·) (logarithmus naturalis) denotes the inverse operation to the exponential function exp(·) and b̅ is a constant that results from the fact that Riemann integrals are definite up to an arbitrary offset. Our result so far reads:
This can finally be prettified by defining an alternative constant b ≡ ln(-b̅) (the initial light intensity), which leads to the following formula, describing how the intensity of light changes while passing through an absorbing volume:
The equation is called Beer-Lambert law. It is used in chemistry to analyse mixtures of chemicals by measuring their absorption behavior (spectrophotometry). The derivation process highlights how it can be advantageous to solve a mathematical problem on an intermediate discrete version of the setup first and transition it back to a continuum afterwards.
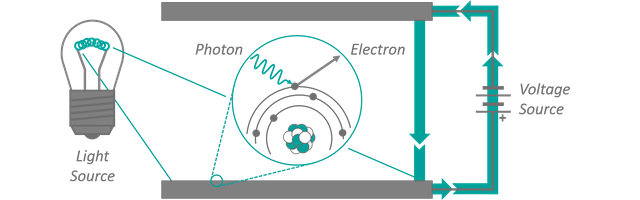
Planck tried something similar, by chopping the energy axis of the cavity radiation problem into small intervals. His hopes were that he could perform a transition to infinitely small steps as well, removing the energy portioning in the end. And he was successful... at least partially. His calculated spectra matched the observed ones perfectly and they contained no trace of an immanent radiation induced apocalypse. There was, however, a small catch. Different from our example, his artificial step size did not vanish. It could not be removed from the result and much to his annoyance even seemed to take on a constant value. The riddle was solved by introducing the concept of energies quanta, i.e. accepting the fact that the artificially introduced energy steps are a real life phenomenon. Instead of assuming that the resonant modes inside the cavity are populated with energy continuously, Planck's findings suggested that their energy content was actually packed in small portions. Only integer multiples of a minimum energy can be found for every frequency. These individually packaged cans of electro-magnetic energy have been named photons. A couple years later Albert Einstein proved experimentally that light can indeed act like particles, by demonstrating the so-called photo-electric effect. Light is shone onto an electrically charged metal surface. Photons from the lamp collide with electrons in the metal, transfer their energy onto them and eject them out of the material. The electrons are then accelerated towards an inversely charged metal plate close by, leading to a measurable current flow between the plates. The experiment setup can be seen in figure 4. To clear up a common misunderstanding: Albert Einstein got his Nobel price in physics for the experimental proof of the particle character of light quanta, not for his work in the field of relativity (the 'E=mc²' business). The non vanishing step size in Planck's calculations was later known as the Planck constant h and it determines how much pre-packed energy a photon with a certain frequency contains. By the way, the letter h hereby stands for the german word "hilfs-variable" which translates to something around the lines of "temporary" or "auxiliary" variable (as Planck originally intended to ultimately sweep it under the carpet). I know... I have been equally disappointed when I learned that a constant as important as Planck's constant carries a name with such profane meaning.
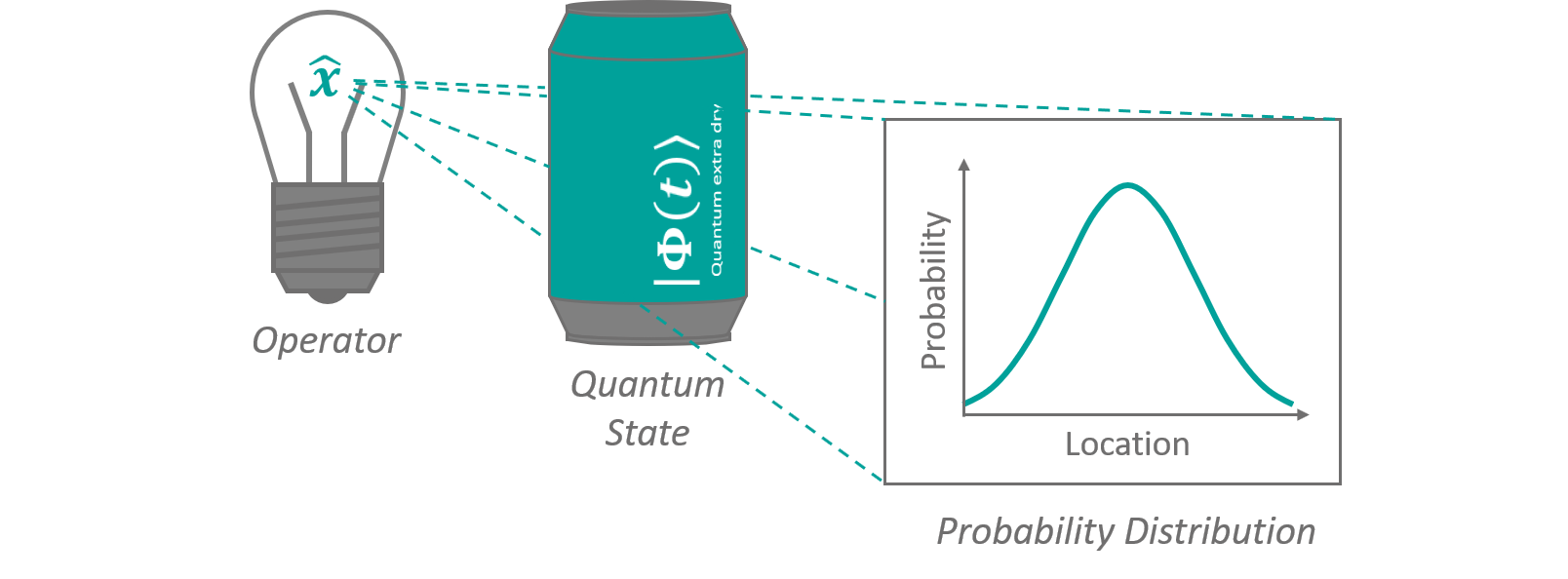
In 1925, after it was well established that light can behave particle like, Louis de Broglie published his thesis, in which he presented calculations based on the assumption that matter itself can behaves like waves. Against common belief at that time, he however thought that these matter waves, as well as other quantum effects, were the result of a so far undiscovered underlying well-defined mechanic. His work didn't receive its due attention, because in the mean time the theoretical description of quantum mechanics through matrix operations gave rise to a quantum theory with a highly non-deterministic (i.e. unpredictable) character. Finally, it was Erwin Schrödinger (the guy with the perpetually dead und not-dead cat) who picked up the concept of de Broglie again and combined matter waves and quantum mechanics into one important equation called Schrödinger equation. What exactly does this equation say about the quantum nature of particles and how to understand it? Without going into too much details, Schrödinger's equation relates how a quantum mechanical state changes over time, in dependance of its total (i.e. all its potential and kinetic) energy. Since the total energy at each point in time usually depends on the state itself, this type of equation (differential equation) can become extraordinarily complicated and is only solvable for a choice few known problems. The concept of a quantum mechanical state is a little bit more difficult to explain. In classical mechanics the dynamics of an object can be described by its intrinsic properties (e.g. mass, charge, etc.) and its path through space in respect to time x(t). For every point in time, the object will be in exactly one place. Using our knowledge about the path, we can deduce all other mechanical properties of the object, like its velocity, forces, its kinetic energie, and so on. In some way x(t) therefore describes a particular classical state, a particle take on. A slightly different setup could potentially lead to a drastically different time evolution. x(t) contains all information about the object... like a beverage can full of 'mechanics soda'. Applying specific mathematical operations to it, translates to shining beams of light through it, projecting out different properties like shadows. A quantum mechanical state is comparable to that. It describes one specific of all possible ways a system of particles will evolve over time in a given setup. The most crucial difference though, is that asking for a particle's property - like its position - will yield some form of probabilistic distribution of many different values (its so-called wave function) instead of just one. This means that quantum mechanics does not give a definite answer (i.e. the particle will be here or there) but a probability of how likely it is to find a particle with its property in the distinct state. See figure 5 for an illustration. In this mathematical model particles are described as little packages that emerge from superposed travelling waves (like in shown in figure 1) on a probabilistic distribution sea.

Where does the uncertainty come from, though? Honestly, we don't have a clue. There exist only possible interpretations of the probabilistic behavior of quantum physics. The most common one is the Copenhagen interpretation which explains the inability of making exact predictions about a quantum state as some sort of indeterminism. In other words, quantum mechanics a is bit like watching the world through an unfocused camera. The blurriness makes it impossible to pin point a value until you measure it directly. All values are possible, each with their respective probability. After you know the actual result, the wave function 'collapses' into the certain value and its probabilistic character is lost. This is a crucial intermediate result: Observing a quantum mechanical state changes it, as you effectively eliminate all other possible outcomes except the one you just obtained. It is important to note, though, that the inability of making deterministic predictions about quantum phenomena in this interpretation is not a disability of the observer. Quantum physics itself carries some sort of intrinsic noise. Other interpretations of quantum mechanics claim that there is only one particle in existence, which travels through space-time via an undiscovered additional dimension. The uncertainty arises from the fact that we can only observe cross-sections through the higher dimensional realm in which this one particle resides. Only a measurement will unveil the particle's full position within the multidimensional space. Even though this sounds like some kind of science fiction, it is one of the more plausible ways of explaining the fact that entangled particles (two ore more particles described by a single, coupled quantum state) will instantaneously transfer changes of their state between each other, even if they are light years apart from each other. Another way of explaining quantum behavior assumes that there exist infinite parallel universes. In every universe the observed particle is in one of its possible settings predicted by quantum theory. Making consecutive observation on fuzzy quantum states is like traversing one of the many possible paths through the parallel universes. The same you on a different track will make completely different observations. With every new observation the current universe splits into as many parallel universes as there exist possible observation results. This leads to a ginormous tree like structure of parallel worlds emerging from every quantum event. An artistic depiction can be seen in figure 6. Every you, in every split universe will think that his observation is the only true one as his timeline will drift away from the other ones and there exists no causal connections to the parallel universe clones. Maybe quantum physics is not random at all, we just haven't figured out, yet, which subtile, omniscient pattern is woven through the strands of our universe causing quantum phenomena.
These rather philosophical thoughts about how our universe might look beyond our consciousness and comprehension conclude the first part of this adventure. In Part II, there will be a run down of some interesting effects that arise from the mysterious properties of quantum physics. Stay tuned.