Calculating Mass from Orbits

steve-d (38)in #science • 6 years ago

Here's a great webpage showing data regarding stellar orbits in our galaxies central parsec-
http://www.galacticcenter.astro.ucla.edu/animations.html

The reason that this is interesting is that it tells us that there is a mass at the galactic centre of 8.2e+36 kg (4.1 million times the mass of our sun) contained with a radius of 6.25 light hours based on the orbits of the surrounding stars and no known astronomical object other than a black hole can contain this much mass in this volume of space (strictly speaking, a black hole with this much mass would have a Schwarzschild radius (or event horizon radius) of ~ 41 light seconds based on r_S=2Gm/c² but there's still no mechanism known that would support a structure of this mass within 6.25 light hours).

It's actually quite easy to calculate the mass of an object from something in (reasonably) stable orbit around it when relativity isn't involved (i.e. extreme gravity and spin) using basic Newtonian equations. Take for example the earth, by simply looking at the moons orbit, the mass of the earth can be calculated. First, take two basic equations for gravity and centripetal acceleration, both in m/s²-

Gravity (a_g)= G(m₁·m₂)/r²

Centripetal acceleration (a_c)=(v²·m₂)/r

where G is the gravitational constant, m₁ is the object being orbited, m₂ is the object in orbit, r is the distance between the two objects and v is the tangential velocity of the object in orbit. For a stable orbit, the following needs apply-

a_g = a_c

G(m₁·m₂)/r²=(v²·m₂)/r

The equations can be rearranged relative to m₁-

G(m₁·m₂)=(v²·m₂)r

m₁=(v²·r)/G

Note that m₂ cancels out so the mass of the object in orbit plays no part in the calculation. Substitute with the quantities for v and r for the moon, in this case, v=1022 m/s and r is the semi-major axis (an approximation of the distance between the moon and earth), r=3.844e+08 m and this provides a reasonable approx. figure for the mass of earth-

m₁=6.0168e+24 kg

Considering the mass of the earth is 5.9722e+24 kg, the figure provided is accurate to within less than 1% difference, which in terms of cosmology is a reasonable approximation. The same equation can be used to calculate the mass of the sun using any planetary orbit in the solar system up to Neptune (it starts to break down slightly with Pluto, possibly due to Pluto's slightly eccentric orbit which would require more complex math). Interestingly enough, you can get a very accurate estimate of the earths mass from the ISS orbit.

If we include for extreme gravity, then relativity has to be taken into account and the equations are rewritten as-

Gravity (a_g)= G(m₁·m₂)/(r²·√(1-2Gm/rc²))

Centripetal acceleration (a_c)=√(1-2Gm/rc²)·(v²·m₂)/r

where √(1-2Gm/rc²) is a component of the Schwarzschild metric and m is equivalent to m₁ (the Schwarzschild metric was one of the first exact solutions to Einsteins field equations that demonstrated that mass-energy can curve spacetime). Note that as r approaches the Schwarzschild radius (r_S=2Gm/c²) gravity increases exponentially and centripetal acceleration reduces exponentially therefore an object in orbit requires much more tangential velocity to stay in stable orbit. The velocity required for a stable orbit is-

v_s=√(Gm/(r·(1-2Gm/rc²)))

This reduces to the Newtonian equation in non-extreme environments (v_s=√(Gm/r). Note the the final most stable orbit for a black hole (for light at least) is 3M (where M=Gm/c², referred to as a geometric unit of mass or gravitational radius) or 1.5 r_S where v_s=c, this is referred to as the photon sphere. For an object with mass, the innermost stable circular orbit (ISCO) is at 6M for a static black hole.

Here it's tricky to solve for m₁ as it ends up on both sides of the equation so more advanced math is required.

Things get more complicated as spin is introduced. In extreme cases, frame dragging (a phenomena where spacetime itself is dragged around the block hole) has to be taken into account if the orbit is close to the spinning black hole. For a rotating black hole, a quantity called a is introduced which is referred to as a geometric unit of spin or spin parameter, a=J/mc where J is the angular momentum. A black holes spin can be measured by a/M, for a static black hole this is 0, for a black hole with 'maximum' spin, a/M is 1. There are only stable orbits in the equatorial plane for rotating black holes and the equation for the velocity required, which is derived from Kerr metric, is-

v_s±=(r²+a²2a√(Mr))/(√(Δ)[a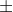r√(r/M)])

where Δ=r²+a²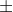-2Mr, the subscript s± for v denotes which direction the orbit is, + for with the frame dragging (using the top symbols for the , signs) and − for against the frame dragging (using the bottom symbols), v_s being much greater against the rotation than with it. This reduces to the Schwarzschild solution for a static black hole

The math would increase in complexity for elliptical orbits that are not on the equator and pass through the equatorial plane of a rotating black hole as shown in the video and on the website (though in this case, the orbits appear to be far enough away from the black hole for the frame dragging not to have too much effect). One source implies that the super massive black hole at the centre of our galaxy has a spin parameter of a/M=0.65 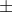0.05 (the spin parameter is normally calculated by establishing where the innermost stable circular orbit (ISCO) is which normally coincides with the inner edge of the accretion disk, this can vary from 6M for a static black hole (a/M=0) to 1M for a maximal black hole (a/M=1). A maximal black hole is considered unlikely due to the violation of a number of black hole thermodynamic laws and the max spin parameter is often considered to be 0.998).