Fraktale - Aufgaben zur Ähnlichkeitsdimension

Mal etwas anderes für alle, die gerne rechnen und vertiefen hier die Möglichkeit die in meinem letzten Post beschriebene Ähnlichkeitsdimension anzuwenden um die fraktale Dimension einiger Fraktale zu berechnen. Lösungen gerne in die Kommentare.

a) Koch-Kurve

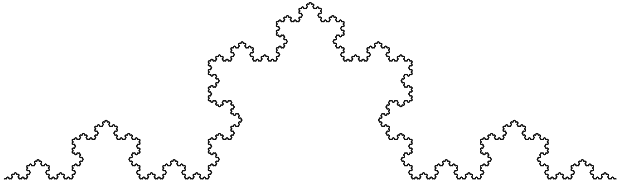
b) Cantor-Menge

c) Hexaflake

d) Sirpinski-Teppich

e) Minkowski-Fraktal

Hier noch ein paar dreidimensionale, das Prinzip bleibt jedoch gleich.

f) Sirpinski-Pyramide

g) Menger-Schwamm

Alle Muster sind nur ein paar Iterationen dargestellt und das Muster muss sich ad infinitum vorgestellt werden.

Viel Spaß beim denken und rechnen.