The attack on the biggest problem of computer science has failed

Three weeks ago, professor Norbert Blum from Bonn (Germany) believed to have solved the famous P-NP problem. Now he withdraws his proof.

© tiero / Getty Images / iStock

For weeks, computer scientists and mathematicians were in turmoil. Norbert Blum, a renowned scientist from the University of Bonn, had presented a proof on the Internet on August 11, with which he wanted to solve the probably most famous puzzle of computer science: the so-called P-NP problem.

The solution would have had far-reaching consequences for computer science and would have made Blum a millionaire. After all, P-NP is one of the seven highly remunerated "Millennium problems". But now Blum has withdrawn his commentary.

The proof is wrong,

writes the Bonn professor on the Internet platform Arxiv, on which his essay stood before.

The complexity of Sudoku

The P-NP problem is about the question of whether difficult problems can be solved by efficient algorithms. Problems become more complex with increasing size. A Sudoku puzzle, consisting of nine boxes, can be solved very quickly, in contrast to one consisting of 144 boxes. For problems that belong to class P ("polynomial"), the solution time increases polynomially - and thus efficiently - with the length of the problem.

Problems associated with NP ("non-deterministic polynomial") are more complex. They are distinguished by the fact that their solution is efficiently verifiable. But so far, computer scientists have not found any efficient algorithms to find a solution to NP problems. Think of the big Sudoku puzzle: It is difficult to solve, since there are a lot of possible ways to solve the problem that a computer has to check all in sequence. As soon as you have a solution, it is easy for a computer to check its correctness.

For at least 45 years, computer scientists have been wondering whether NP problems are really P-problems. In this case, NP problems could also be solved efficiently, you only have to find the respective algorithms. This would have far-reaching consequences, as, for example, modern encryption methods are based on a NP problem.

The evidence is linked to the 1980s

Blum presented in his work a proof of the prevailing opinion that P and NP are not the same - the encryption procedures and other NP problems remained brain-teasers. For his reasoning, he tackled a problem that was in NP and tried to show that there is no algorithm that solves it efficiently. Thus, P and NP would unambiguously disagree. To prove that a problem can not be solved efficiently, he generalized and extended the results of the theoretical computer scientist Alexander Razborov from the 1980s.

Clique Problem

The clique problem describes the task of finding the maximum number of nodes within a graph that are directly adjacent. The figure shows an algorithm for solving the clique problem. In this case, the clique number is four. © Thore Husfeldt at English Wikipedia / Brute force Clique algorithm / CC BY-SA 3.0 CC BY-SA

This had proved that the so-called clique problem from NP can not be solved in polynomial time if only limited logical operations are allowed for its solution. Bills of all types can be represented by circuits - that's how computers count. In general, there are three logical operations within these circuits: AND, OR, and NOT. In electrical circuits, they decide whether and how electricity flows through them.

P-NP seemed to be close at hand

At that time, many experts believed that Razborov's work was very close to the general proof that P is not NP, and finally, only the non-operation in the circuits was missing. But then the computer scientist Alexander Andreev realized that the so-called matching problem, which does not permit an efficient solution for monotonous circuits, is solved by polynomial time circuits - and thus lies in P. This led a proof that P is not NP, far away.

Blum believed in his work to have found a way to deal with Andreev. He argued that for a particular type of problem that mathematicians can construct by an approximation method, statements about monotonic circuits apply to general circuits. Mathematicians have in the past derived the clique problem about this approximation method, but not the matching problem. In this respect Blum's theorem benefits. Thus, he argued that since no monotonous efficient algorithm solves the clique problem, there is no general efficient algorithm. Thus P would be non-NP without contradicting Andreev's work.

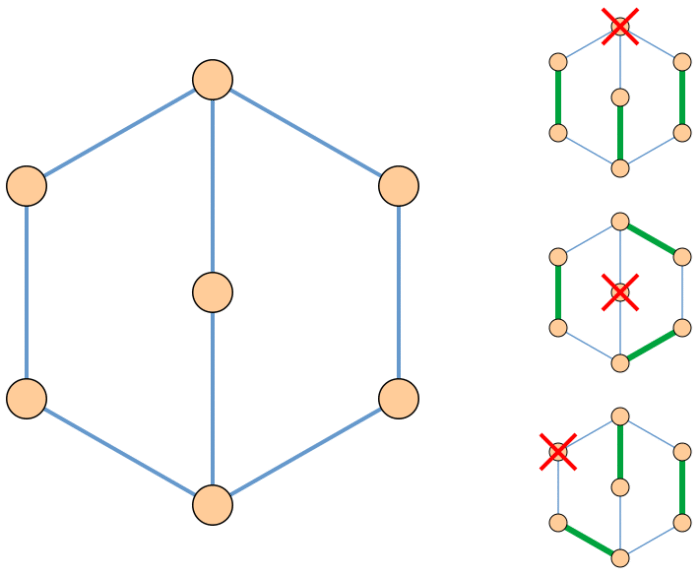
Matching Problem

In the Matching Problem, the largest possible number of pages must be found within a graph that does not end at the same node. On the right in the figure, they correspond to the pages marked in green. In either case, one node can not be paired with another. © David Eppstein, 2008 / public domain

Did Blum look at the work of a Hungarian colleague?

Evidently, however, Blum did not know the work of the Hungarian mathematician Eva Tardos. It once introduced an abstract function to show that monotonic and general circuits are very different. Tardos defined the function named after her by means of the approximation method and showed that the solving time for monotonic circuits exponentially increases with the input length.

Following Blum's proof, the Tardos function should be in NP. In 1988, however, Tardos showed that its function is in P and thus an efficient algorithm exists for the solution. This would disprove Blum's evidence. In the informatics forum stackexchange, a user named "idolvon" is arguing to have found the error in Norbert Blum's proof. Blum himself soon wants to comment on his website. And who knows: Perhaps he succeeds in saving his proof.