What exactly is the "P=NP?" problem?

Lots of people I know have heard or seen this "equation" somewhere, wondered what it actually meant, but didn't bother looking it up. In this post I hope to elucidate on the ideas behind this.

If you're a CS major, this post may not be for you.

The basics

---

In theoretical computer science, algorithm performance is measured using a technique called "Asymptotic analysis" . It is the increase in the amount of time required for a program to run as you keep increasing its input size to infinity.

This kind of analysis is popularly known as the "big O" notation, which is the upper bound on the algorithm - the maximum time it will take for it to run. In other words, it is the worst case scenario. These are inputs that make the program "work the longest" to give an output and terminate . For an example, consider a linear search on an array where the numbers are arranged in ascending order, and you ask the program to find the largest number, it is going to take the maximum time because the largest number is at the last index - the program has to check numbers at each index position from the start, before finally getting to the last index position. This is how linear search works, there are of course, other algorithms that optimize the performance (reduce run time) significantly, by working in "clever" ways. (Note that giving an input value that doesn't exist in the array is also a worst case scenario)

Take a look at this random graph I looked up on Google, this shows asymptotic growth rates

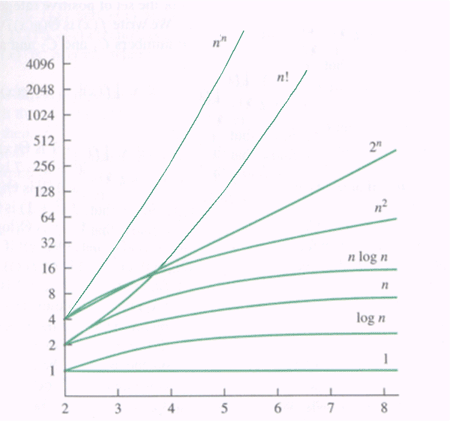
On the x-axis is the input size, y axis is the time. "n" denotes the input data size. Time is measured in the number of operations* an algorithm would take, as a function of input data size n , it is known as complexity.

For the curve "1", there is no change in time taken for the algorithm to run as the input size grows- this isn't really a practical case as most problems one works with in real life vary in performance with varying input sizes. For the log n curve, there is growth, but very little, and almost falls flat for larger values of n. This is usually the mark of a very efficient algorithm. On the other hand, consider the 2^n, n! and n^n curves, a slight increase in input size causes exponential growth in time needed.

*an operation is any basic operation for a particular task. It could be a comparison, like in sorting algorithms, addition, like in k-sum problems or multiplication, like in matrix multiplication etc.

For a better perspective, the n^2 curve doubles for each increase in n, i.e, the time required doubles just by increasing input data size by 1. The n^n grows even faster than that, even for relatively small values of n, the curve will be moving almost vertically, like a rocket !

If there is a constant in the exponent of the run time - it is known as "polynomial growth", which is essentially the "P" in the title. P is the class of all algorithms that have a polynomial growth rate.

When the exponent has an input-size dependence (n in exponent), it is known as "NP" - or non-deterministic polynomial time, exhibits exponential growth. These grow much faster relative to polynomial-time algorithms, since there is combinatorial explosion involved.

(note: term like "log n" in the exponent is something in between polynomial and exponential. It is called "quasi-polynomial" or "pseudo polynomial" growth rate)

Why is this important?

---

You might now wonder why bother about how the running time of an algorithm grows (whether polynomially or exponentially) as the input size n goes to infinity. It gives us no information about the number of steps required to compute the output for definite values of n (a constant - like a million or a billion etc) which would be more practical.

Well, the “number of steps” is not a generic measure, because it varies too much from one machine to another, depending on the hardware and on the low-level programming details. The asymptotic complexity of an algorithm could be seen as a completely theoretical metric, something which is totally independent of technology. It sets bounds on computational efficiency, for example , if we have built the fastest computer that performs operations at the speed of light and use it to test run a program for increasing n values, the "time taken" would still grow based on the asymptotics (algorithm efficiency) - the same math applies to our hypothetical supercomputer too.

Obviously, the real-world software design requires taking into account several other non-asymptotic or "practical" factors of a program’s efficiency, like the compiler overhead, cache layout etc. But most programmers know asymptotics matter as well.

Turing machines

---

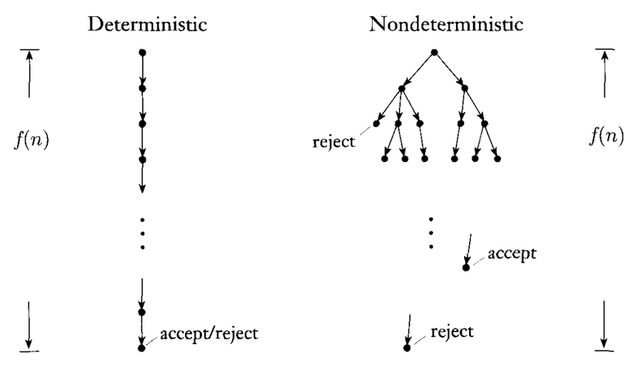
You may have noticed the use of the term "non-deterministic" in order to explain "NP". So, what does deterministic vs. non-deterministic mean in this context mean?

For that, we'll need to know what a Turing Machine (TM) is.

From wiki-

A Turing machine is an abstract machine that manipulates symbols on a strip of tape according to a table of rules; to be more exact, it is a mathematical model of computation that defines such a device. Despite the model's simplicity, given any computer algorithm, a Turing machine can be constructed that is capable of simulating that algorithm's logic.

The machine operates on an infinite memory tape divided into discrete cells.The machine positions its head over a cell and "reads" (scans) the symbol there. Then, as per the symbol and its present place in a finite table of user-specified instructions, the machine (i) writes a symbol (e.g. a digit or a letter from a finite alphabet) in the cell , then (ii) either moves the tape one cell left or right , then (iii) (as determined by the observed symbol and the machine's place in the table) either proceeds to a subsequent instruction or halts the computation.

Basically, at any given point in time, the TM is in a particular state and it scans what is present on the cell of the infinite memory tape, and depending on what it scans from the cells, it writes a symbol ( e.g digit or letter) on the cell, moves the tape one cell forward or backward, and goes into a different state. This is called a "state transition".

The fascinating part is that, we can construct any computer by cleverly designing states and transitions. Which is the equivalent of any computer program that can be written, so this abstract construction is used as a theoretical model of a computer, which essentially tells us what computers can or cannot do.

A deterministic TM only has one possible transition at each state and each symbol that it is scanning from the memory tape. All our computers are deterministic TMs with finite tapes. Whereas a non-deterministic TM is capable of multiple state transitions at each state, i.e, it can "check" several transitions at once, kind of like "visiting" all possible branches (decision points in the program) simultaneously without having to revisit states. Non-deterministic TMs do not exist in the real world (perhaps Quantum computers may change that), it is an imaginary model.

This picture I pulled from Google illustrates their difference

P=NP?

---

We know that any problem that a non deterministic TM can solve, can also be solved on a deterministic TM. Now, the question "P=NP?" asks

"If a problem takes polynomial time on a non-deterministic TM, is there an algorithm that will solve the problem in polynomial time on a deterministic TM? "

Until now, no one has been able to show that such an algorithm exists, or prove that such algorithms are impossible. It remains one of the major unsolved problems in Theoretical CS and Mathematics.

If any one NP problem, say A, can be solved in polynomial time , "P=NP" becomes true, since it has been proven that all NP problem can be reduced to A by a technique called polynomial-time reduction.

Most computer scientists believe that P!=NP, that is, it is impossible to write an algorithm for any NP problem that has polynomial time complexity.

One of the most popular examples of an NP problem is the Boolean satisfiability problem. It is actually quite simple to understand, and write an algorithm to solve, but most likely impossible to write an algorithm that runs in polynomial time.

It is the problem of assigning values to a boolean expression such that it evaluates to true. A k-SAT (k-satisfiability) problem is a generalization of the problem and doesn't specify the number of variables and the maximum "clause size" allowed in the Boolean expression. (2SAT, 3SAT, 4SAT etc) are the specific problems.

2SAT is the only k-SAT problem which is solvable in polynomial time. Here's a nice, accessible explanation for why it is so.

Scott Aaronson has once said that "P=NP?" is the equivalent of asking whether human creativity can be automated , since if P=NP, there is no fundamental difference between verifying a solution and finding one, or between appreciating and creating something, there is no creative leap , anyone could solve/create anything if given the right instructions.

---

Relevant link for further reading :

https://www.quora.com/What-is-the-fundamental-reason-that-proving-P-%E2%89%A0-NP-is-so-difficult